降雨入渗作用下填埋场边坡稳定性分析
席永慧 王化祺 郭丽南 张广年
(同济大学建筑工程系,上海 200092)
0 引 言
随着自然资源不断被开发利用和社会文明的不断发展,特别是人口的增长和高度向城市集中,以及城市化的迅速发展,世界各国的城市垃圾以快于其经济增长近3倍的平均速度增长。近年来我国414个城市的垃圾以平均每年10%的速度猛增,我国城市垃圾产生量占全世界城市垃圾年产量的30%,每年产生将近2亿吨的城市垃圾,城市生活垃圾堆存量已达70亿吨[1]。无论是发达国家还是发展中国家都不可避免地受到垃圾成灾的严重威胁,并因此付出高昂的代价。在众多的垃圾处理方式中,卫生填埋法因其各方面的优点被建设部和科委于1991年9月正式确定为我国推广的首选技术。目前,我国已建成660多个垃圾填埋场。每年消纳垃圾1.2亿多吨,占我国垃圾处置总量的70%以上[2]。
卫生填埋法表现出不安全性,垃圾灾害类型复杂,发生量大、扩散面广、蔓延较快、危害很大,易造成土壤污染、水体污染和大气污染,严重威胁人体健康。垃圾灾害时有发生,如英国高达244 m的威尔士阿伯芬垃圾场曾滑入城里,导致800多人伤亡;1960年前后,美国曾有500多处垃圾堆体发生灾害[3]。垃圾堆体滑坡失稳的灾害时有发生,如2000年7月10日,马尼拉垃圾填埋场因连降暴雨而滑塌,死亡百余人,受伤者千余人,塌下的垃圾厚度高达10 m;2002年6月14日,重庆沙坪坝凉枫垭垃圾填埋场因暴雨而滑塌,40万m3的垃圾将山坳碎石厂的三层建筑物吞没,死亡10人[2]。在众多垃圾填埋场可能发生的灾害中,滑坡是极其重要的一个方面,而降雨入渗是边坡稳定性的重要影响因素,Koerner 等对10起填埋场灾害进行分析,发现大量填埋场失稳是由渗滤液引起的[4]。
从20世纪20年代开始,渗流对工程的影响受到工程界的广泛关注。许多研究者相继进行了大量研究工作,并取得大量颇有价值的研究成果。垃圾填埋场边坡静力稳定分析最早于1991年由Mitchell等提出,他们对美国加州Kettleman山的一个垃圾填埋场进行了土工稳定分析,并提出了填埋场设计施工的指导建议[5],此后国内外学者对填埋场边坡稳定问题进行了许多研究工作,取得了显著的成果。邱文经计算研究发现,非饱和土边坡的稳定性基质吸力有着密切的关系,当基质吸力随着外界环境发生变化时,边坡的稳定性也随着发生改变[6]。曾玲等提出一种基于饱和-非饱和渗流及非饱和抗剪强度理论的路堤边坡稳定性分析方法,并利用该方法对算例边坡的降雨入渗过程及瞬态稳定性进行了研究[7]。天津大学刘晓立[2]基于降雨入渗对垃圾边坡的渗流作用,考虑垃圾土体的土工特性与一般意义上的土体的显著的区别,研究了降雨作用下的垃圾填埋场边坡的稳定机理和破坏模式。张文杰等[8]结合苏州七子山垃圾填埋场的工程项目,通过室内试验量测垃圾饱和渗透系数和土-水特征曲线,推导了渗透函数,计算结果表明:推导出的渗透性函数可以用于垃圾的非饱和-饱和渗流分析。基于简化降水边界,结合饱和-非饱和渗流理论,Chao等利用有限元软件模拟了雨水渗流作用下的边坡问题[9]。张广年研究发现降雨持时及降雨强度是影响边坡稳定性的两个重要方面。土的入渗能力是斜坡的稳定性重要控制因素,暴雨属于多少年一遇及暴雨的降雨量决定了暴雨对斜坡稳定性的影响。降雨渗流影响具有一定的范围,长期且连续的降雨对边坡稳定性影响较大[10]。
总结现有研究成果可以发现,针对降雨入渗作用下垃圾堆体的边坡稳定分析与计算的研究并不多见,因此本文拟通过理论与工程实例相结合,研究降雨入渗下填埋场边坡稳定性的理论体系,研究降雨持时、强度、模式对边坡稳定性的影响,并通过工程实例对其进行验证和修正。本文研究内容将进一步完善我国在填埋场降雨渗透作用机理、设计方法和工程应用等方面的研究成果,为相关规范的编制提供理论和实践依据,为填埋场的新建、改建和扩建等进一步应用提供宝贵经验,对低碳经济的施行和可持续的发展起到重要的推动作用。
1 垃圾土的土水曲线与渗透性函数
垃圾具有大孔隙,是高度非均质材料,其渗透特性不同于一般工程上的土,一般认为优势流的发生使其中的水分运移规律更加复杂[11]。R.Stegmann和H.J.Ehrigtv[12]指出:随着垃圾的降解和压缩,填埋场内介质逐渐均质化,孔隙体积减小,在年久的垃圾中优势流的发生几率大大降低,这时垃圾中的渗流较符合达西定律,类似于多孔介质中的非饱和一饱和渗流。W.A.Straub和D.R.LynchIsl[13]最早将非饱和渗流理论应用于对垃圾填埋场的研究;G.P-Korfiatis等[14]以Richard非饱和渗流方程为基础,建立了一维非饱和渗流数值模型。虽然上述研究对含水量、基质吸力和渗透性的关系仅进行了简单描述,但其对非饱和渗流理论在垃圾填埋场领域的应用方面则进行了很有价值的尝试。Stoltz利用原始实验设备,研究了经历压缩并完成多孔介质结构演变的城市固体废弃物的保水性,并得出了不同样本的保水曲线图[15]。Reddy等利用数值二相流模型,预测经受渗滤液回灌的不饱和MSW的水力特性(含水率和孔隙水压力)、力学特性(应力-应变关系)和填埋场垃圾流体的耦合作用[16]。
张文杰等[8]结合工程项目,通过室内试验测定了垃圾的饱和渗透系数和土-水特征曲线,在此基础上推导了其渗透性函数,具有一般性,结果可以应用于垃圾土的饱和-非饱和渗流分析。
张文杰等为了解垃圾的持水特性,对埋深3~5 m处的垃圾进行了压力板仪试验,所得垃圾土-水特征曲线如图1所示。
由于垃圾具有大孔隙特性,大孔隙中的水很容易排出,故垃圾的土-水特征曲线在基质吸力较低(接近0 kPa)时为陡降段,故垃圾的进气值接近于0 kPa,这是新鲜垃圾的土-水特征曲线的一个重要特征。

图1 垃圾土的土-水特征曲线Fig.1 Soil-water characteristic curve of waste soil
垃圾高度非均质的特性决定了难以直接量测垃圾的非饱和渗透系数,故采用间接方法。如前所述,垃圾的非饱和渗透性系数kw是孔隙水压力(或体积含水量)的函数,用Campbell公式[17]计算不同体积含水量时垃圾的渗透性:
(1)
式中:ks为饱和渗透系数;Se为有效饱和度;θ为体积含水量;θs为饱和含水量;n为拟合常数,且有n=3+2/λ,其中λ可由Brooks-Corey公式,通过土-水特征曲线上任两点的基质吸力与体积含水量值求得;θr为残余含水量,由实验结果可知:θr=33%。
Brooks-Corey公式可表述为
(2)
式中:ψ为基质吸力;ψc,λ均为待定常数。
从土-水特征曲线上取代表性的两点(如ψ=1 kPa和33 kPa及其对应的θ值),解式(2)得到ψc和λ两个拟合常数,并将其代入式(1)后可得渗透系数kω与含水量θ的关系,由土-水特征曲线上基质吸力与含水量的对应关系,得到渗透系数与基质吸力的关系曲线,即渗透性函数曲线(图2)。
从图2可以看出,随含水量降低,垃圾渗透系数急剧减小,推导出的渗透性函数在基质吸力较小时存在陡降段,这是因为大孔隙中的水排出导致过水截面积比减小,垃圾的渗透系数由于渗流路径挠曲度急剧增加而迅速减小。

图2 垃圾土的渗透性函数曲线Fig.2 Permeability function curve of waste soil
2 降雨对于填埋场边坡稳定性的影响实例分析
2.1 基本模型及分析方法描述
根据上海市老港填埋场现场实际情况,选择基本模型的几何尺寸如图3所示。

图3 基本模型的几何尺寸(单位:m)Fig.3 Geometry size of basic models (Unit:m)
图3中,坡度为1∶2,垃圾土堆载高度为20 m,在软件模拟过程中,需要分析降雨入渗情况下坡度、垃圾土堆载高度对边坡稳定性的影响,因此会根据需要在模拟过程中调整坡度及堆载高度。
数值模拟过程中,垃圾土及下层粉质黏土的各项物理参数按表1来取。
表1垃圾土及粉质黏土的各项参数

Table 1Parameters of waste soil and silty clay
垃圾土的土-水曲线及渗透性函数采用上文中中图1和图2的数据,粉质黏土的土-水曲线及渗透性函数采用Fredlund-Xing等式[18]进行模拟,取a=300 kPa,m=1,n=1。
数值模拟过程中,降雨通过边界流量来实现。假设排水良好,表面无积水,降雨参数的选取按规范GB 50014—2006采用,通过计算,本文选取特征降雨持时为1 h、8 h、24 h、120 h,特征降雨强度为6×10-7m/s 、2×10-6m/s、5×10-6m/s、2×10-5m/s。
边界条件的设置为:bc,fg,aj的边界流量为0 m/s,ab、gj的总水头H=-1 m,cd,ef的边界流量为降雨强度q,de的边界流量为30.5×q/2(随着坡度不同做相应修改)。
初始条件的设置为地下水高度-1.00 m,首先假设降雨量为0。
GeoStudio是一套专业、高效而且功能强大的适用于岩土工程和岩土环境模拟计算的仿真软件。在本文对于填埋场边坡稳定性分析中,首先使用SEEP/W进行稳态渗流,而后进行暂态渗流,最后将所得孔隙水压工况导入SLOPE/W中进行稳定性分析。
2.2 数值模拟结果及分析
2.2.1孔隙水压力随时间的变化
按图3建立模型,将前述各节参数输入,在模拟降雨前,使用稳态分析软件计算出初始边坡空隙水压力,结果如图4所示。

图4 初始孔隙水压力(单位:kPa)Fig.4 Initial pore water pressure (Unit:kPa)
将降雨强度取为5×10-6m/s,进行瞬态分析,可得到不同时间的孔隙水压力,以8小时后的空隙水压力为例,如图5所示。

图5 经过8小时降雨后孔隙水压力(单位:kPa)Fig.5 Pore water pressure after 8 hours rainfall (Unit:kPa)
2.2.2降雨强度和降雨持时对边坡稳定性的影响
将2.2.1中所得孔隙水压力代入Slope/W软件中,可计算得出边坡稳定性系数随着时间的变化曲线,结果见图6,图中一、二、三、四等降雨分别对应前述4种降雨降雨强度:6×10-7m/s 、2×10-6m/s、5×10-6m/s、2×10-5m/s。

图6 边坡稳定性系数随时间的变化曲线Fig.6 Slope stability coefficient curve changing with time
由图6可以看出,随着降雨强度的增大和降雨的持续,稳定系数在逐渐减小。在降雨初期,稳定系数下降较快,因初期雨水入渗使坡体内负空隙水压力大幅减小,导致抗剪强度等相应减小,稳定系数随之大幅下降。而在降雨初期,垃圾土的含水率不高,决定其入渗能力有限,二、三、四等降雨在初期表现相似,可以理解为,二等降雨已满足其入渗需求,降雨强度的提高无法使得入渗量增加,提高部分的降雨量将形成坡面径流而排走。降雨初期阶段过去之后,边坡稳定系数随着时间的推移成一定比例逐渐降低,并且降雨强度越大,比例越大。
在实际中,降雨并不一定是均匀强度的,会有不同模式,本文选取三种降雨型进行模拟,分析了在不同降雨模式下边坡稳定性系数的变化曲线。
根据实测天气降雨情况,选取各时段降雨强度见图7。模拟分析结果见图8。
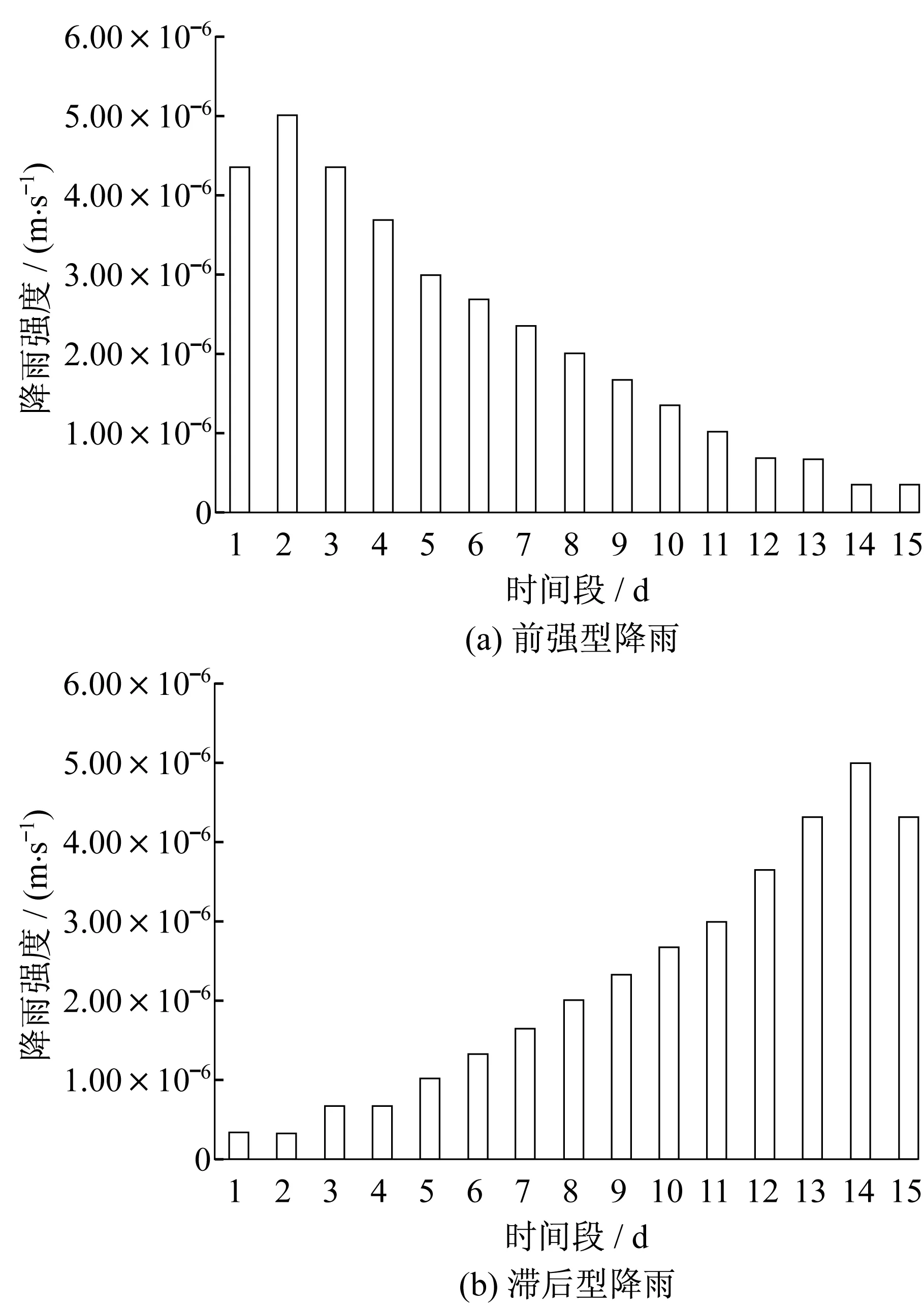
图7 三种降雨型在各时间段降雨强度Fig.7 Rainfall intensity of three rainfalls in each period
由图8可以看出,三种降雨型相比,滞后型降雨对于边坡稳定性最不利,其次是标准型,这与Rahimi的结论基本相似[19]。推测由于前强型降雨在早期由于渗入速率有限,会造成多数降雨随坡面排走,这对于边坡的稳定性是有利的,而滞后型降雨在降雨末期达到最大降雨强度,此时由于之前的降雨使得渗入速率提高,则强降雨发挥其最大作用,使得安全系数急剧降低,这与图8中滞后型降雨的安全系数变化曲线相吻合。
在标准型和前强型降雨模式下,在前120小时降雨结束前安全系数就已经开始升高,这是由于随着降雨减弱,雨水的入渗量开始减弱并小于垃圾土中雨水的流失量,使得安全系数升高。而滞后性型降雨则是降雨强度急速减小为零,则没有这样一个缓慢变化的过程,所以其在120小时降雨结束时,安全系数相比于前强型和标准型升高较快,但由于前期降雨作用,其相同时间内安全系数仍比另外两种雨型要小。

图8 在三种降雨型作用下边坡安全系数随时间的变化曲线Fig.8 Slope stability coefficient curve changing with time of three rainfalls
本文数值模拟分析结果表明,滞后型降雨对于边坡稳定性最不利。在实际工程中,施工单位或运营管理单位需要密切关注天气情况,如果遇到滞后型降雨且降雨强度较大,需要及早结合Slope/W软件进行填埋场边坡安全性计算,根据降雨强度计算填埋场边坡的稳定性安全系数。如填埋场边坡稳定性安全系数过小,则需采取疏干降水、削坡减载、反压坡脚或人工支挡等加固措施。
3 结 论
本文建立了降雨入渗渗流作用下的垃圾填埋场边坡稳定计算模型,结合上海地区的降雨特性,获得四等降雨强度、不同坡度、不同堆载高度和不同降雨模式下边坡安全系数随时间变化曲线,结果表明:
(1) 随着降雨时间的推后,导致入渗降雨在坡脚的暂时积聚,进而在坡脚处垃圾土体达到饱和状态。
(2) 随着降雨强度的增大和降雨的持续,稳定系数在逐渐减小。在降雨初期,稳定系数下降较快,且降雨强度达到一定范围之后,提高降雨强度无法使得入渗量增加,提高部分的降雨量将形成坡面径流而排走。降雨初期阶段过去之后,边坡稳定系数随着时间的推移成一定比例逐渐降低,并且降雨强度越大,比例越大。
(3) 在标准型和前强型降雨模式下,在前120小时降雨结束前安全系数就开始升高,这是由于随着降雨减弱,雨水的入渗量开始减弱并小于垃圾土中雨水的流失量,使得安全系数升高。而滞后性型降雨则是降雨强度急速减小为零,在120小时降雨结束时,安全系数相比于前强型和标准型升高较快,但其相同时间内安全系数仍比另外两种雨型要小。
在三种雨型中,滞后型降雨对于边坡稳定性最不利,其次是标准型。在实际工程中,施工单位或运营管理单位需要密切关注天气情况,如果遇到滞后型降雨且降雨强度较大,填埋场边坡稳定性安全系数过小,则需采取疏干降水、削坡减载、反压坡脚或人工支挡等加固措施。

