旋转机械损伤跟踪的改进相空间曲变法

牛 乾， 杨世锡， 甘春标

(浙江大学 机械工程学院， 杭州 310027)

旋转机械广泛应用于机械、能源、石化、冶金、航空等不同领域，是应用最为广泛的一类机械系统。同时旋转机械部件(如转轴、轴承等)的故障也常常是导致设备最终失效的重要原因。对旋转机械损伤演化过程的在线跟踪，可以为旋转机械的故障预测和健康管理提供有益的参考，及时掌握设备当前损伤程度，降低设备使用风险，减少不必要的维护成本，提高设备使用效能。随着机械设备的高速化和高精度化发展，同时由于其机械系统的复杂性，强非线性，运行工况的不确定性以及强背景噪声，旋转机械部件的损伤演化动力学特性变得十分复杂。常用的线性振动分析方法以及传统的时频、频域、时频域信号特征难以对系统动力学行为和损伤状态之间的关系给出一个十分合理的解释。

利用非线性动力学理论和方法是解决这一问题的有效途径。传统的非线性特征，例如最大李亚普诺夫指数[1]、关联维数[2]等，可以检测到动力系统因损伤造成的状态变化，但是不适用于连续跟踪系统损伤的演化过程[3]。Chelidze等[4]提出了相空间曲变(PSW)的方法，指出可以以重构相轨迹的动态演变表征动力系统参数的缓慢变化。胡雷等[5-6]用此方法对单一工况和变工况下的轴承故障进行了跟踪。Qian等[7]用相空间曲变量为特征提出了一种多时间尺度的轴承寿命预测方法。Segala等[8]应用该方法对长时间重负载行走情况下人体物理机能的疲劳状态进行了跟踪和预测。但是PSW法需要大量的计算时间，无法实现对系统损伤演化过程的实时跟踪[9]；并且跟踪结果可能会产生较大的波动和误差，对相近的损伤状态可能无法辨别。

基于旋转机械运行具有周期性的特点，本文提出一种改进的相空间曲变法。通过相位对应避免了原PSW法对重构相空间中每一个点都进行最近邻点寻找计算。以矢量平均模型代替了原PSW法中的局部线性模型，以减小模型参数拟合的计算量。当得到损伤跟踪矩阵后，提出了一种基于经验模态分解(EMD)[10]的损伤演化过程信息提取方法，以去除原PSW法跟踪结果的波动。本文方法可以大幅减小原PSW法的计算量以实现系统损伤状态的实时跟踪；并使跟踪结果变得更加平滑准确，对相近损伤状态有更好的分辨能力。

本文通过数值模拟Rössler方程产生参数慢变的非线性振动响应数据；以螺栓去除法产生不同深度的裂纹，模拟裂纹转子系统不同的损伤状态，采集系统的振动位移数据；此外通过滚动轴承由健康到故障的退化实验，采集轴承的振动加速度数据。对模拟数据和实验数据分别应用本文方法和原PSW法，对系统的损伤演化过程进行跟踪，验证本文方法的有效性和优越性。

1 损伤跟踪的相空间曲变理论

含有慢变损伤的动力学系统可以简化为一个分层演化的快-慢耦合系统

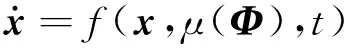
(1a)

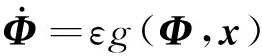
(1b)

式中：x∈Rn为系统快变量(如，振动信号、应力信号等)，能够通过测量得到；Φ∈Rm为损伤演化过程慢变量(如，磨损程度、裂纹长度等)；f(·)和g(·)分别为快变系统函数和慢变系统函数；μ(·)为损失变量Φ的函数；t为时间；ε为区分快慢变量时间尺度的小比率常数。在工程实际中，损伤演化过程Φ通常是难以直接通过测量得到的，因此我们的目的就是通过测量得到的系统快变信号x对慢变损伤演化过程Φ进行识别、跟踪。

1.1 基于系统响应的损伤跟踪原理

处于损伤状态的系统从某一初始状态为(t0,x0,φ0)(本文只考虑单一损伤变量的情况)，经过很短的预测时间tp=t-t0后，其响应为x=X(tp,t0,x0,μ(φ0);ε)。对处于参考状态(健康状态)的系统，经过同样短时间tp后响应为xR=X(tp,t0,x0,μ(φR);ε)。通过比较两者的不同得到短时参考模型预测(STRMP)误差eR，以定量表征系统的动态演化。

eR=X(tp,t0,x0,μ(φ0);ε)-X(tp,t0,x0,μ(φR);ε)

(2)

当预测时间tp很短时，此时间段内系统的损伤变化可以忽略，由式(1a)表示的快变子系统可视作是平稳的。此时式(2)中的系统响应项可以用正则摄动展开为

(3)

式中：Xn为展开后各阶幂级数εn的系数，且有X0为原系统退化问题(ε=0)的解X0=X(tp,t0,x0,μ(φi);0)；O(·)表示高阶无穷小函数；φi为φ0或φR。将式(3)代入式(2)可得，

eR=X(tp,t0,x0,μ(φ0);0)-

X(tp,t0,x0,μ(φR);0)+O(εtp)

(4)

对式(4)右侧第一项在φ=φR处进行泰勒级数展开得到结果如下

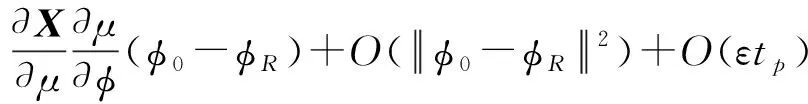
(5)

忽略高阶无穷小项，得到如下近似关系

eR≈C(tp,t0,x0,φR)φ+c(tp,t0,x0,φR)

(6)

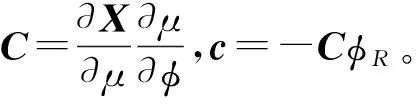
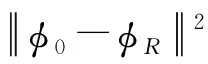
1.2 损伤跟踪函数的计算

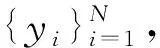
y(i)={yi,yi+τ,…,yi+(d-1)τ}T

(7)

式中：d为足够大的嵌入维数，τ为时间延迟。如果时延过小，则各重构向量会十分相近而包含过量的冗余信息；反之各重构坐标会变得完全不相关。相应地，嵌入维数需要足够大以使得重构相轨迹不交叉，相空间充分展开；而嵌入维数过大则会增加不必要的计算量本文以伪最近邻法确定最佳的嵌入维数[12]，根据平均互信息曲线的第一个极小值来估计时间延迟[13]。

重构的状态向量受限于一个未知映射P:Rd→Rd

y(i+1)=P(y(i);φ)

(8)

对于重构相空间中的任意一点，定义其跟踪函数为单步参考模型预测误差

eR(y;φ)=P(y;φ)-P(y;φR)

(9)

不同损伤状态下相空间轨迹的发展方向变化是由损伤状态的细微变化引起。式(9)中P(y;φ)可根据每个数据段直接得到，将式(8)代入式(9)可得

eR(y;φ)=y(i+1)-P(y;φR)

(10)

然而，P(y;φR)只能由参考数据段的点得到，对于其他数据段，需要根据参考数据段估计来获得。在文献[4]中使用了局部线性模型来进行拟合

P(y(i);φR)≈Aiy(i)+bi

(11)

以y(i)在参考相空间内的Nm个最近邻点及其一个时间步长后的响应点对Ai和bi进行最小二乘估计。那么利用单步参考模型预测误差估计得到损伤跟踪函数

eR(y;φ)≈y(i+1)-Aiy(i)-bi

(12)

1.3 损伤演化过程信息的提取

在计算各个损伤状态数据段中各个点的损伤跟踪函数后，将每个数据段(对应于各个损伤状态)的损伤跟踪函数作为一个行向量，形成一个包含有系统损伤演化过程信息的跟踪矩阵。原PSW法使用了标量跟踪或矢量跟踪两种方法来从跟踪矩阵中提取出损伤演化过程。

标量跟踪是对行向量的各损伤跟踪函数求加权均方根

(13)

式中：M=N-(d-1)τ为损伤相空间的总点数

(14)

式中：r(y)为采用式(11)求映射P时选取的若干个最近邻点中距离最远点的距离，dp为这些近邻点所组成子空间的关联维数。

矢量跟踪是采用平滑正交分解(SOD)的方法，从跟踪矩阵中提取局部方差最小(最平滑)，总体方差最大(能量最大)的慢变损伤演化过程。对于同时存在多损伤变量的动力系统，SOD可以提取出各个损伤变量的演化信息；而且此方法不需要对损伤演化过程的模型有先验知识，只需假设损伤演化过程是遵循某一平滑缓慢的趋势。

2 改进的相空间曲变法

在工程实际中，旋转机械系统的振动响应具有周期性。当旋转机械运行周期不变时，采用等周期采样可以得到每个周期采样点数相等的数据集；当运行周期变化时，采用等相位采样，也可以得到同样特点的数据集。对于此类数据集，本文提出了如下改进的PSW法。

2.1 改进的损伤跟踪函数计算方法

为了减小原损伤跟踪函数的计算量，以实现系统损伤演化过程的实时跟踪，本文提出了一种改进的损伤跟踪函数计算方法如下。

y(i;φR)={x(i;φR),

x(i+τ;φR),…,x(i+(d-1)τ;φR)}T

(15)

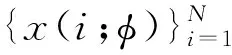
y(i;φ)={x(i;φ),x(i+τ;φ),…,

x(i+(d-1)τ;φ)}T

(16)

在参考相空间中寻找与损伤相空间第一个点y(1;φ)欧式距离最邻近的一个点，假设这个最近邻点是参考相空间中的第j个点，即此点为y(j;φR)

(17)

我们认为y(1;φ)和y(j;φR)为损伤相空间与参考相空间中的同相位点。由于采用整周期等相位采样，损伤相空间中的任意一点y(i;φ)便与参考相空间中的点y(i+j-1;φR)以相位一一对应起来。假设一个周期内的采样点数为n，以矢量平均模型代替原PSW法的局部线性模型，估计参考相空间的映射P如下

P(y(i);φR)≈

(18)

式中：k为用以拟合映射P的周期数，即采用参考相空间中相应点的前、后各k个周期内的同相位点来估计映射P。矢量平均模型避免了原PSW法中局部线性模型的参数拟合计算。以此矢量平均模型计算得到改进的损伤跟踪函数如下

eR(y;φ)≈y(i+1;φ)-

y(i;φ)-P(y(i);φR)

(19)

对于无损伤、系统运行稳定的参考相空间，当k较大时有P(y(i);φR)≈P(y(i+n);φR)。因此只需要计算一个周期内n个点的映射P即可，其余点的映射P分别约等于其在此周期内同相位点的映射P。

需要说明的是，文中应用原相空间曲变法需要选择Nm个最近邻点用以拟合局部线性模型。拟合点选取过少则可能无法准确拟合模型，过多则可能包含入大量不相关的伪近邻点造成拟合误差，本文参考文献[4]选取16个最近邻点。同样地，本文提出的改进方法选取16个周期的同相位点计算矢量平均模型，且后文中这两个参数均取16。用以重构相空间的数据长度需要有足够多的周期数(≥16)用以拟合局部线性模型，且反映出系统可能存在的复杂非线性动力学特性；而数据量过则多会增加不必要的计算量。

采用原PSW法计算损伤跟踪函数，需要对损伤相空间中的每一个点寻找其在参考相空间中的Nm个最近邻点，再进行局部线性模型的拟合。假设损伤相空间和参考相空间的总点数都为M=N-(d-1)τ，则计算一个损伤状态下M个损伤跟踪函数，需要计算M2次欧式距离，进行M次M个点的排序，并计算M个局部线性模型。因此，原PSW法计算量很大，难以满足实时识别、跟踪系统损伤状态的需求。而采用本文方法计算一个损伤状态下M个损伤跟踪函数，只需要计算M次欧式距离，进行1次M个点的排序，计算一个周期n次矢量平均模型。本文方法减少了M(M-1)次欧式距离计算，M-1次排序计算，M-n次映射模型计算。在实际应用中，需要足够多的数据点来计算损伤跟踪函数，当M较大时，本文方法可以大幅减少原方法的计算量。在配置为Core i7-2620M CPU主频为2.70 GHz，内存为4.00 GB的计算机上，以MATLAB软件计算一个损伤状态100 000个点组成的3维相空间的损伤跟踪函数。原PSW法用时2 411.01 s，本文方法用时1.26 s。可见本文方法可有效减少计算时间，满足在线监测的需求。

另外，原PSW方法在选择Nm个最近邻点时，有些近邻点可能是由于时间邻近而造成空间距离邻近的伪近邻点[14]。这些伪近邻点会造成由局部线性模型估计映射P时产生较大的误差，进一步降低损伤跟踪函数的准确性，可能使相近的损伤状态难以区分。而本文方法选择一个最近邻点后使各个点以相位一一对应，从而避免了将时间邻近点选为空间距离邻近点而产生的误差，使得对映射P的估计更为准确。

2.2 改进的损伤演化过程信息提取方法

采用原PSW法标量跟踪和矢量跟踪两种损伤演化过程信息提取方法虽然可以得出系统损伤演变的整体趋势，但是跟踪结果可能有起伏和波动，难以辨别相近的差异较小的损伤状态。为了使提取的损伤演化过程更为平滑、准确，且对相近的损伤状态具有更好的分辨能力，本文基于EMD提出改进的损伤演化过程信息提取方法如下。

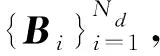
(20)

式中：M为损伤相空间的总点数。将每个数据段(对应不同的损伤状态)j(j=1,2,…,Nr)相对于各个参考子空间的Nd个平均损伤跟踪函数集合起来组成一个Nd维跟踪向量

ej=[e1(φ),e2(φ),…，eNd(φ)]

(21)

计算全部Nr个数据段的跟踪向量，再按照数据段的时间顺序张成跟踪矩阵Y如下

Y=[e1;e2;…;eNr]

(22)

Y为一个Nr×Nd的矩阵，对其每个列向量进行EMD分解，提取各列向量分解结果的趋势项di(i=1,2,…,Nd)。对所有Nd个趋势项求矢量平均得到跟踪的损伤演化过程Φ

(23)

将参考相空间分割成多个子空间，可充分利用相空间各局部所包含的损伤演化过程信息，再利用EMD提取出各损伤趋势信息，可去除原PSW法跟踪结果的波动，使得跟踪结果更加平滑，对相近的损伤状态具有更好的分辨能力。Chelidze等中选取Nd=27，本文计算发现Nd=10时与Nd=27时计算得到的损演化伤跟踪结果相差很小，为了减少计算量在后文计算中均选取Nd=10。

3 损伤跟踪的数值模拟验证

本文通过数值模拟Rössler方程产生参数慢变的非线性振动响应数据[15]，验证本文提出的改进的PSW法。在数值模拟中，通过缓慢改变一个参数的值表征系统慢变的损伤演化过程。Rössler方程如下

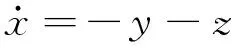
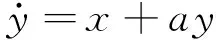
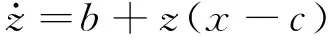
(24)

其中，令b=0.6，c=6.0，a以正弦函数从0.1变化到0.4，取50个a值表征50个不同的损伤状态。计算50个数据段，每个数据段取10 000个稳态响应的数据点。此系统y方向响应的分岔图，如图1所示。当a值表征的损伤程度逐渐严重，系统的响应由单周期变成多周期和混沌。由于系统的响应呈现出复杂的非线性特征，传统的线性分析方法和时域、频域、时频域特征难以对系统损伤状态进行跟踪。

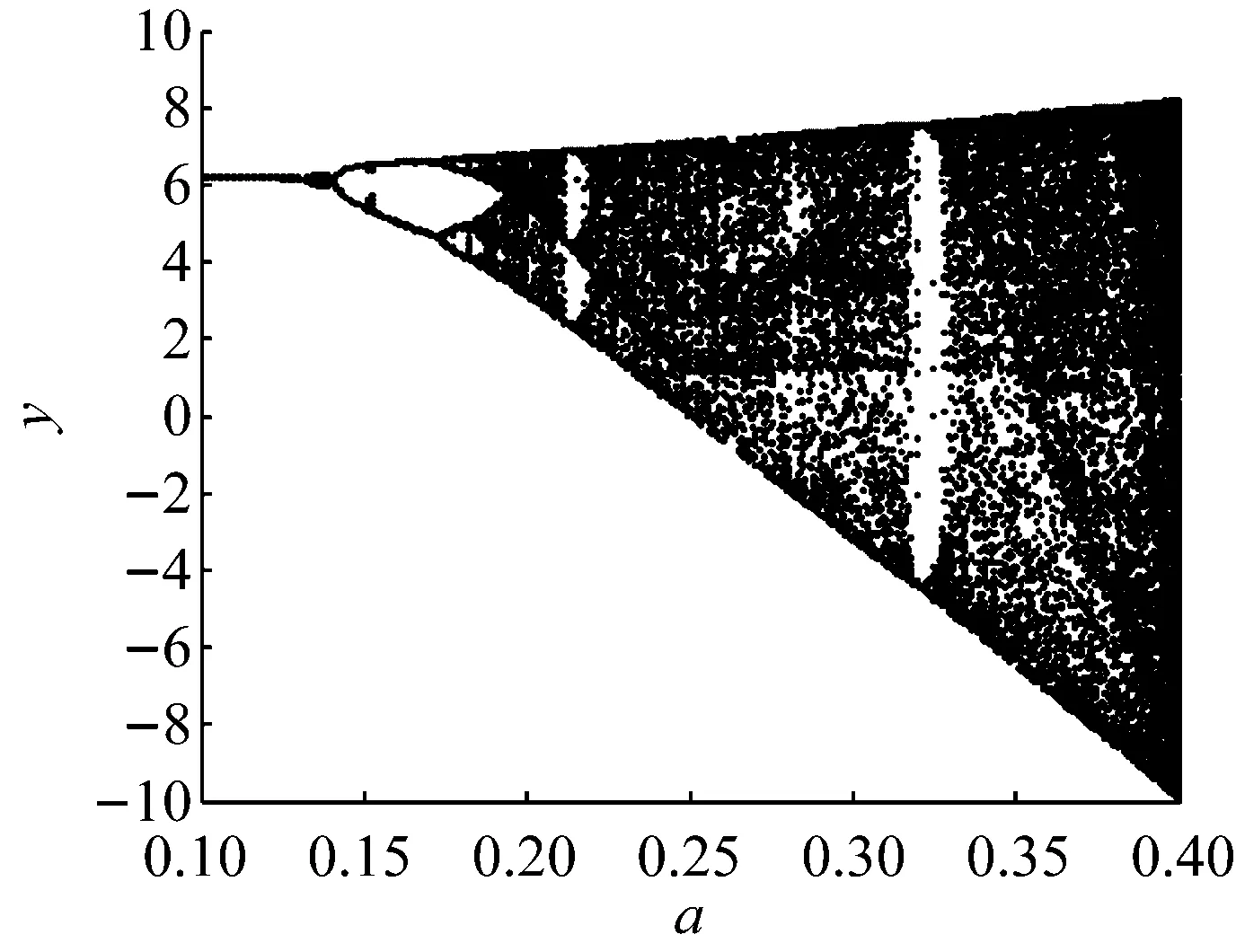
图1 Rössler系统y方向响应分岔图

对模拟数据分别使用原PSW法的标量跟踪、矢量跟踪和本文方法，跟踪系统损伤演化过程。为了便于结果比较，对各方法计算得到的损伤演化过程Φ进行线性归一化

(25)

式中：ΦL为归一化损伤程度，取值在[0,1]区间内。后文中各方法的结果比较均采用归一化结果。同样对由a值变化表征的实际损伤演变过程进行归一化，各方法结果比较如图2所示。

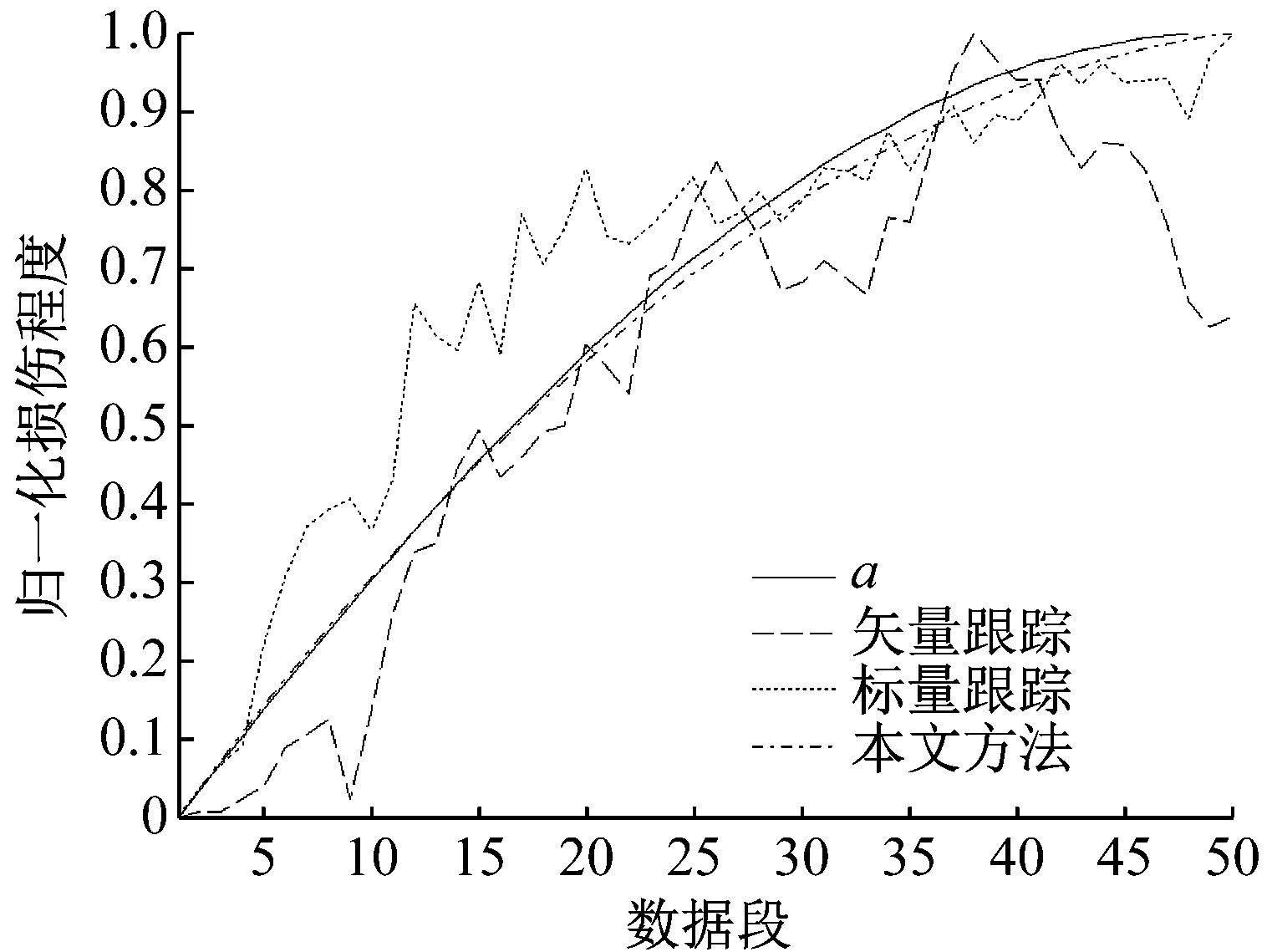
图2 模拟数据各方法跟踪结果比较

由本文方法得到的跟踪结果与a值实际的变化过程十分接近，计算相关系数为0.99。用传统PSW法标量跟踪和矢量跟踪方法得到的跟踪结果整体趋势与a值实际的变化过程相同，相关系数分别为0.95和0.94；然而对于有些损伤状态跟踪偏差较大，且跟踪过程不够平滑，有较大波动，导致原PSW方法对相近的损伤状态难以区分。

4 损伤跟踪的实验验证

本文通过实际采集旋转机械运行时的振动响应数据进一步验证本文方法的有效性和优越性。以裂纹转子和轴承为实验对象，采用本文方法跟踪其损伤演化过程，并与原PSW法进行比较。

4.1 裂纹转子实验

本文以去除螺钉法模拟不同深度的转子表面横向裂纹，以表征裂纹转子系统不同程度的损伤状态。文献[16]通过转子振动实验，定性和定量地验证了采用去除螺钉法模拟实际疲劳裂纹的可行性。本文以螺钉全部拧紧时的振动响应作为参考(健康)状态，以分别去除1，2，3个螺钉表征3个损伤程度逐渐加重的损伤状态。采用机械故障综合模拟实验台(SQI-MFS)进行实验，系统转速为20 Hz，用电涡流传感器和LMS数据采集系统采集各个状态转子的振动响应数据，采样频率为16 kHz。实验装置如图3所示。

4个状态下裂纹转子竖直方向振动响应的时域波形和频谱图分别如图4(a)和(b)所示，由时、频域振动响应难以区分出裂纹转子系统不同的损伤状态。一次实验采集每个状态下裂纹转子系统竖直方向振动响应的10 000个数据点，得到包含4×10 000采样点的一组实验样本，分别应用本文方法和原PSW法以及振动幅值的均方根(RMS)计算跟踪结果。实验在同样条件下进行10次共采集得到10组样本，对10组样本的各方法的跟踪结果进行归一化后求均值和标准差，归一化后的均值结果如图5所示，标准差如表1所示。重构相空间的时延τ=75，嵌入维数d=7，分别根据互信息法和伪最近邻法得到。由于损伤状态很少，不能产生行向量足够多的跟踪矩阵，难以应用矢量跟踪方法和基于EMD的损伤演化过程信息提取方法，所以这里只比较本文方法和传统PSW法的标量跟踪结果。此外，由于转子水平方向振动响应计算得到的结果与竖直方向相一致，这里不再列出。

图3 实验装置

(a) 波形图

(b) 频谱图

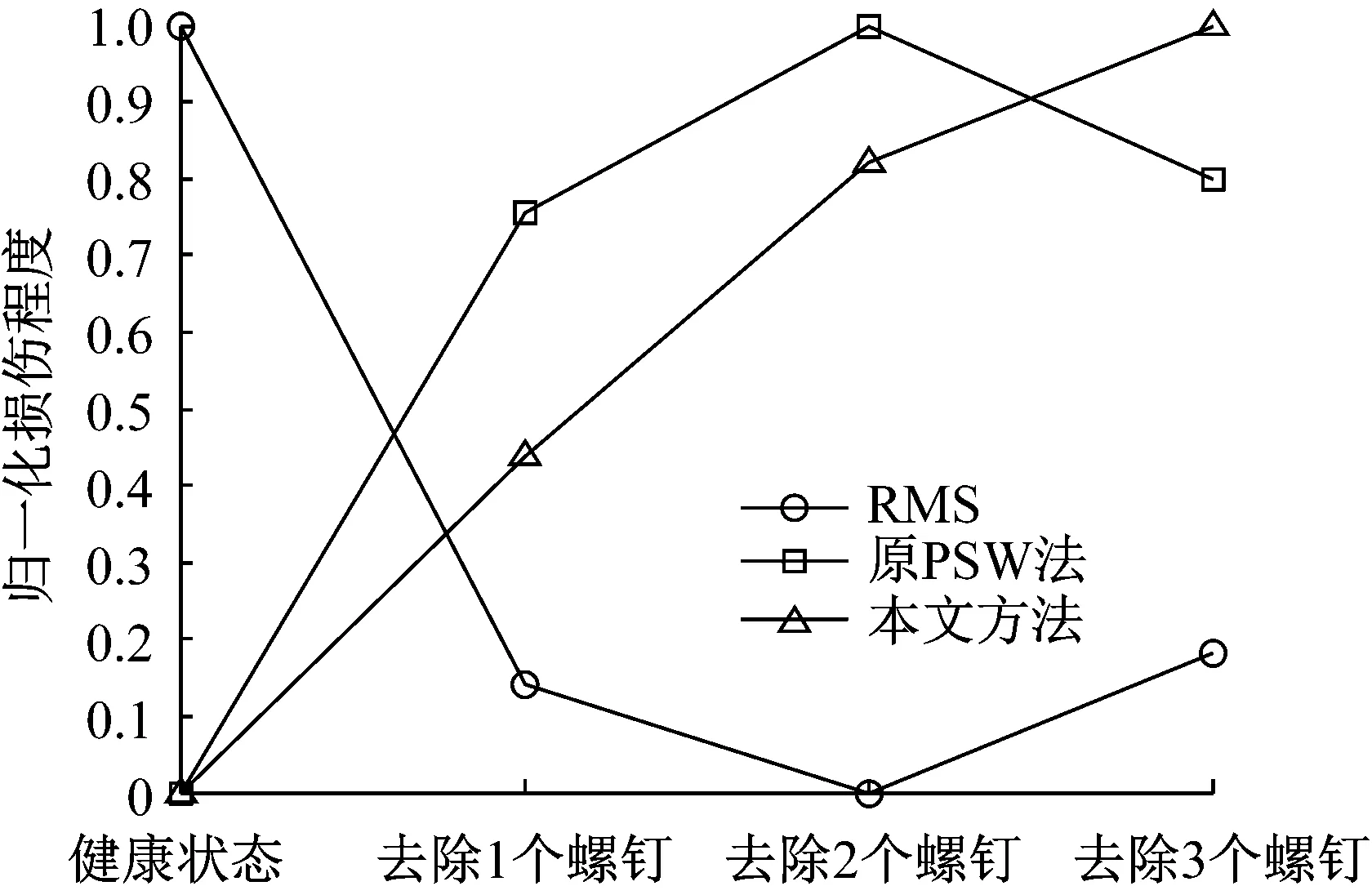
图5 裂纹转子各方法损伤跟踪结果比较

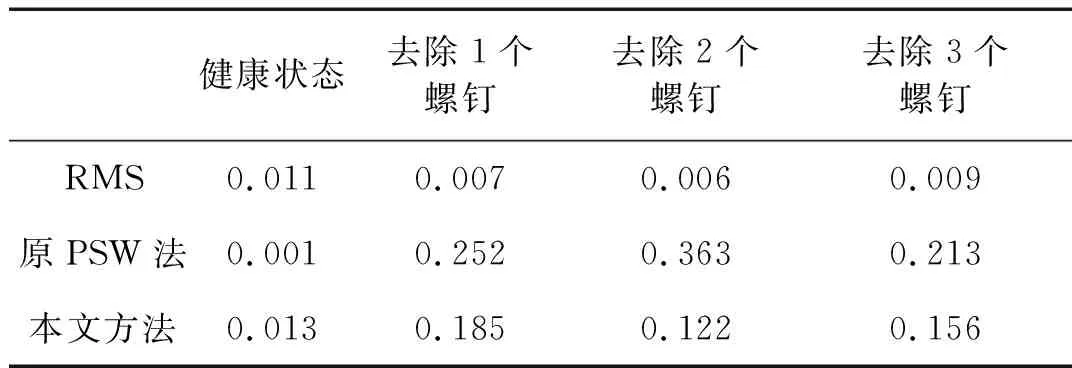
健康状态去除1个螺钉去除2个螺钉去除3个螺钉RMS0.0110.0070.0060.009原PSW法0.0010.2520.3630.213本文方法0.0130.1850.1220.156

由图5所示，各损伤状态的RMS无法跟踪损伤程度逐渐加重的损伤演化过程。原PSW法虽然跟踪了损伤加重的趋势，但是对于去除3个螺钉的损伤状态没有识别，难以与去除1个螺钉和2个螺钉的损伤状态相区别。而本文提出的方法成功跟踪了损伤加重的过程，且对各损伤状态有很好的辨别度。原PSW法对去除3个螺钉的损伤状态难以识别的原因可能是在选择邻近点时错误的将有些时间邻近点当作了空间邻近点，造成拟合的局部线性模型产生较大误差。由表1所示，对于10组样本，各个状态下裂纹转子振幅RMS的标准差均很小，说明在同样实验条件下采集得到的10组样本间差异较小。除了健康状态，原PSW法计算结果的标准差要大于本文方法计算结果的标准差，说明由原PSW法计算得到的标量损伤跟踪结果的波动程度要大于本文方法。

4.2 轴承退化实验

本文采用智能维修系统NSF I/UCR中心实验产生的轴承退化数据[17]进一步验证本文提出的方法。实验装置的转速为2 000 r/min，实验轴承受到的径向载荷为6 000 kN。4个双列轴承(轴承1-4，型号：ZA-2115)安装在转动轴上进行实验，通过加速度传感器(型号：PCB353B33)采集轴承振动信号。每隔10 min以采样频率20 kHz采集一次数据得到一个数据文件，一个数据文件包含20 480个采样点。

第一个测试从2004年2月12日10:32进行到2004年2月19日6:22。在实验结束时轴承1出现外圈故障，采集轴承1振动加速度一共得到了984个数据文件。第二个测试从2003年10月29日14:39进行到2003年11月25日23:39。在实验结束时轴承3出现内圈故障，采集轴承3振动加速度一共得到了2 000个数据文件。对两个测试实验得到的振动加速度数据分别应用改进的跟踪函数计算得到改进的标量跟踪结果以及基于EMD的损伤演化信息提取方法计算得到改进的矢量跟踪结果，并与原PSW法的标量跟踪、矢量跟踪结果进行比较，结果归一化后如图6所示。重构相空间的时延τ=3，嵌入维数d=5，分别根据互信息法和伪最近邻法得到。

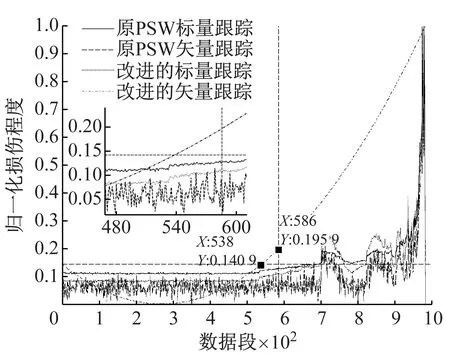
(a) 测试1

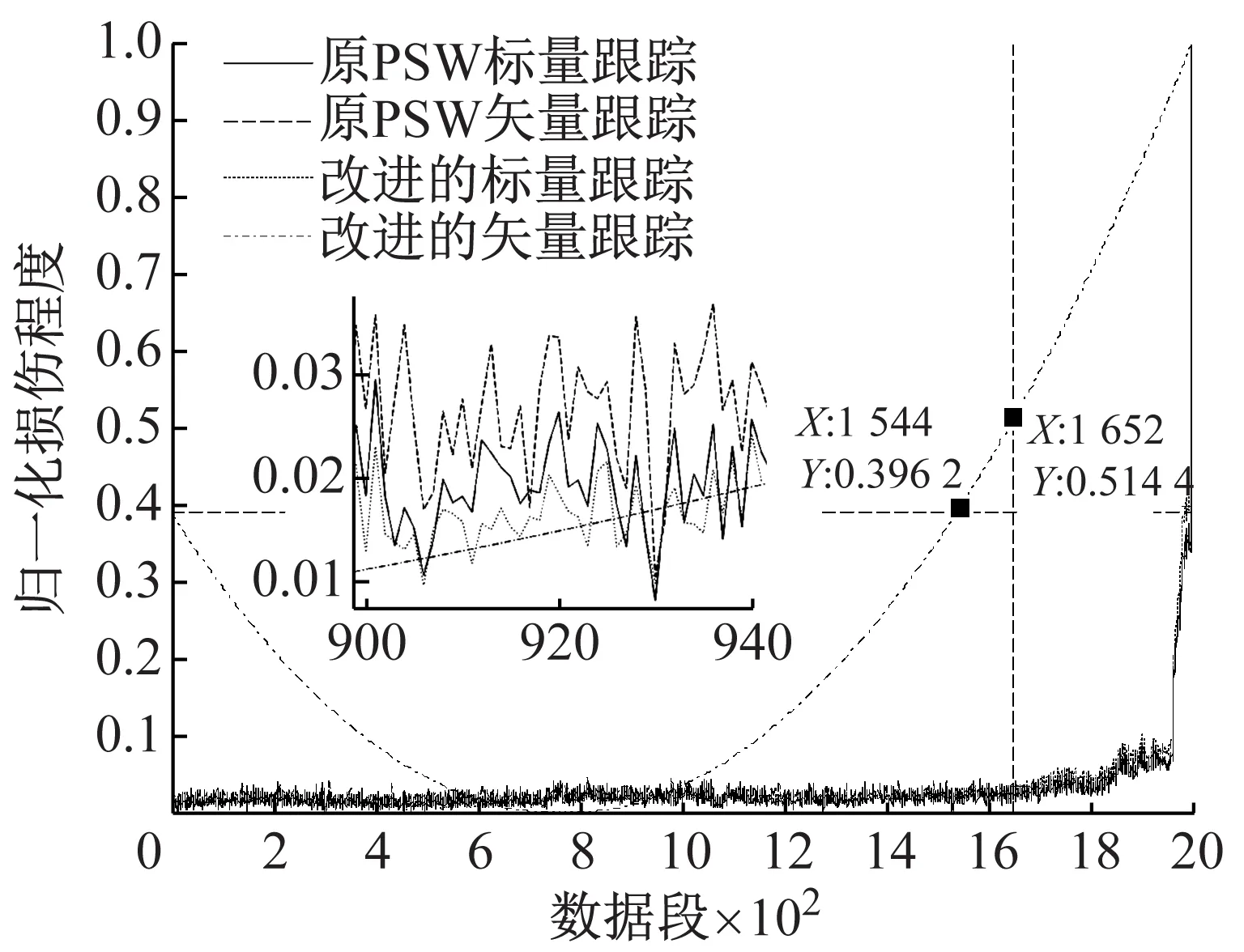
(b) 测试2

胡雷等分别用轴承损伤的数值模拟数据和实验数据验证了原PSW矢量跟踪和标量跟踪的有效性。如图6所示，原PSW法和本文方法都可以跟踪轴承损伤程度逐渐加重的趋势过程，本文改进的标量跟踪与原PSW标量跟踪结果十分接近，但本文改进方法的计算量远小于原PSW法，详见2.1节。此外，原PSW法和改进的标量跟踪曲线均有波动，尤其是测试1中原PSW矢量跟踪结果波动很大。跟踪结果的波动使得相近的不同损伤状态有同样的损伤特征值而无法区分,严重影响初始故障点的识别和剩余有效寿命的准确预测。而本文矢量跟踪得到的光滑跟踪曲线则可以有效区分相近的损伤状态。

在图6中，竖直的虚线为参考文献[19]中的故障初始点，由切比雪夫不等式方法计算得到。本文改进的矢量跟踪过程可提供一种简便的不需要先验知识的轴承初始故障点识别手段：就是以损伤跟踪过程中达到初始损伤程度的点为初始故障点。如图6所示，此方法确定的初始故障点接近且略早于文献[19]中的初始故障点，可提供及时的轴承故障预警。当存在先验知识时，可通过机器学习等方法使初始故障点更接近实际情形，这有待进一步的研究。综上所述，基于本文方法计算得到的改进的标量跟踪和矢量跟踪结果，可以为旋转机械实时运行状态监测以及剩余有效寿命预测提供有益的参考。

需要说明的是，初始运行时轴承并无损伤，但是损伤跟踪过程并未从0开始，这是由于归一化运算造成的。由式(25)计算得到的归一化损伤程度是使原跟踪过程中的最小值化为0，最大值化为1；而初始状态的损伤特征值并不是最小值。实际上，由于轴承是运行在一个实验测试系统中，采集到的轴承振动信号不只是反映轴承的运行状况，也会受到整个系统各部件的影响。因此计算得到的归一化损伤程度其实也是整个系统运行状态的反映。在实验初始阶段，虽然轴承未产生损伤，但是由于系统各部件间的磨合使系统运行逐渐稳定，表现出性能指标(损伤跟踪过程)逐渐下降的现象。文献[19]中提取的轴承损伤特征或性能指标在实验初始阶段皆有呈现出下降趋势。本文改进的矢量跟踪结果是一条先单调递减再单调递增的曲线，类似于设备故障率的“浴盆曲线”。在轴承运行的初期阶段，系统运行逐渐磨合趋于平稳，随后长时间的运行使轴承产生疲劳耗损直到出现初始故障。在判断轴承处于损伤特征值递减的初期磨合阶段还是递增的疲劳耗损阶段的基础上，可以根据不同的损伤特征值进一步区分系统的运行状态。目前关于轴承全寿命周期性能退化评估的研究多集中于尽早发现轴承的初始故障点[20]以及初始故障发生后的剩余有效寿命预测[21]。关于轴承初始运行阶段及长时间无故障平稳运行阶段的系统性能评估及剩余有效寿命预测问题还有待进一步研究。

5 结 论

本文基于旋转机械运行具有周期性的特点，提出了一种改进的PSW法，以实现对旋转机械的实时损伤跟踪。通过相位对应和矢量平均模型代替了原PSW法中的局部线性模型，有效减小了原方法的计算量。提出了基于EMD的损伤演化过程信息提取方法，使得到的跟踪结果更平滑准确，且对相近损伤状态分辨能力更强。通过数值模拟以及裂纹转子实验和轴承退化实验验证了本文方法的有效性和优越性。本文方法可为旋转机械实时状态监测以及剩余有效寿命预测提供有益的参考。