高动态场景下频率估计器的设计与实现*

税 敏 ， 苏泳涛 , ， 曹 欢,,4

（1.重庆邮电大学通信与信息工程学院，重庆 400065；2.中国科学院计算技术研究所无线通信技术研究中心，北京 100190；3.移动计算与新型终端北京市重点实验室，北京 100190；4.中国科学院大学，北京 100190）

0 引 言

新的5G标准中，提出了随时、随地接入的概念，拟引入卫星网络对各个地区进行覆盖。卫星常分为高轨、中轨和低轨卫星。高轨卫星与地面处于相对静止状态，其本身运动造成的多普勒频移较小。但是，当用户包含高铁、飞机等高速运动的物体时，它的相对运动造成的多普勒频偏为104～105Hz。不同于高轨卫星，中轨和低轨卫星由于本身的高速运动会造成较大的多普勒频移，若地面终端也是高速运动的终端，那么在卫星通信过程中，信号经信道传输时，会因高速运动造成较大的频偏和相移，使得信号到达接收端无法正常解调和译码。尤其是低轨卫星，移动速度非常快，自身造成的多普勒频移为105～106Hz[1]。将这种处于相对高速运动的状态，简称“高动态”。高动态场景下，多普勒频移不仅大，还因径向速度和加速度随时间不断的变化，而呈现高阶时变特性[2-3]。因此，在进行正常通信前，必须对接收的信号进行估计与补偿，才能有效恢复原始的基带信号，保证可靠的通信。

高动态场景下的载波频偏主要是多普勒频偏。时域经典的频偏估计算法包括M&M算法[4]、Kay算法[5]和L&W算法[6]。理论上均具有超过0.2倍符号速率的估计范围，但均达不到解调译码所需精度。L&R算法[7]和Fitz[8]算法精度较高，但是估计范围小。文献[9-10]设计了一种采用M&M算法、L&R算法和细估计算法级联的频率估计器，使频偏从符号速率的20%逐级收敛。该方法级联次数较多，因此实现复杂度较高。文献[11]采用频率误差检测算法和L&R算法级联完成频偏估计，存在精度和复杂度不可兼得的问题。文献[12]设计了一种采用类M&M算法和ML估计算法实现信号的频率捕获，需要多次运用复数相乘和复数相加，计算复杂度高。

针对高动态场景的特点和以上频率估计器计算复杂度高、频偏捕获范围小、估计精度低等缺点，本文设计了一种高动态场景下的频率估计器，提出了优化后的多级级联频偏估计算法。基于最佳符号间隔理论优化粗估计算法复杂度，利用Kay算法思想扩大了细估计算法的估计范围。

1 系统架构和模型描述

1.1 系统架构描述

卫星通信系统架构如图1所示，包括空间段、地面段和用户端。空间段由一个或多个卫星组成，作为通信中继站，主要起透明转发、星上处理等作用。地面段通常由核心网、地面网络控制中心和信关站组成，主要起资源分配，波束、频谱管理，卫星姿态监控等管理和控制的作用。用户段由用户终端组成。其中，卫星速度根据轨道高度[13]，通过开普勒第三定律计算所得。用户终端速度常见数值，如波音747飞机约940 km/h，普通高铁约300 km/h，快艇速度约60 km/h。

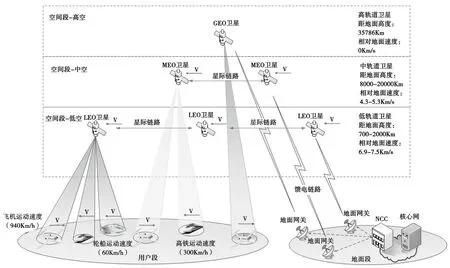
图1 高动态卫星网络架构

多普勒频移主要是由卫星和用户终端的相对运动引起。多普勒频移的表达式可表示为：

其中，fd是多普勒频移，f是载波频率（本文f采用Ka频段频率30 GHz），Vd是卫星与用户终端间的径向相对速度，c是光速。由式（1）和网络中各网元的属性参数可计算出表1数据。

表1 不同场景下多普勒频移参数

根据表1可以看出，低轨的多普勒问题最严重，本文研究重点关注低轨中典型场景的频谱估计。宽带卫星通信频段采用Ka频段（20～40 GHz），不同场景下多普勒频移参数大致如表1所示。在飞机场景下，若采用低轨卫星作为通信中继站，则多普勒频移是载体和卫星的叠加，717.5～777.4 kHz。高动态场景下，多普勒频移不仅大，还存在高阶变化率，仅飞机多普勒漂移达到1 700 Hz/s。为保证接收到的信号能正确解调和译码，在此之前需完成信号的估计和补偿。显然，高动态场景下的频偏估计和补偿最突出。

1.2 信号通信模型

一个完整的数字通信系统由发射机、空口信道和接收机三大部分组成，如图2所示。

图2 数字通信系统

信号到达接收端经下变频、匹配滤波后完成同步。高动态场景下，定时同步和帧同步已取得显著成果，本文只针对载波同步中频率估计进行研究。定时同步和帧同步后，对信号经过提取，此时信号可以表示为：

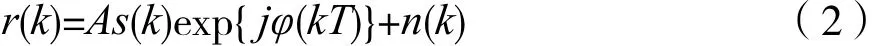
其中A是信号幅度，本文取A=1，s(k)是经相位调制后的第k个调制符号，T是符号周期，φ(kT)是由收发两端载波频率带来的误差，n(k)是复高斯白噪声。

由于接收信号中的调制信息具有与本地调制信息共轭相乘等于1的特点，即s(k)s*(k)=1。因此，表达式（1）可转化为：

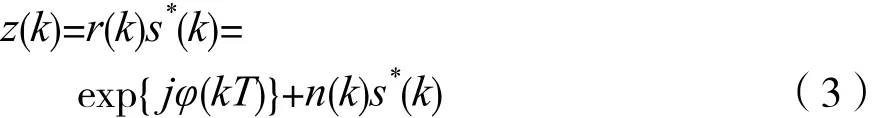
在高动态场景下，频偏具有高阶变化率。通过泰勒级数对φ(kT)进行展开，在忽略3阶以上项时，可得到：

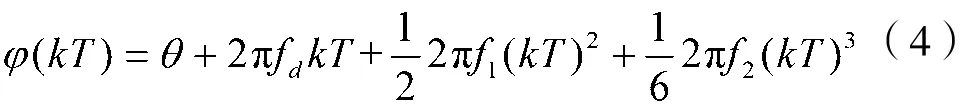
其中θ是初始相位，fd是多普勒频移，f1、f2是频偏的一阶、二阶变化率。本文暂不研究对变化率的估计，因此变化率造成的频偏以扰动δ的形式体现，即：

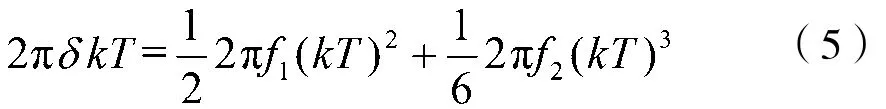
设初始相位为0，且将噪声部分作近似处理，可将表达式（3）转化为：

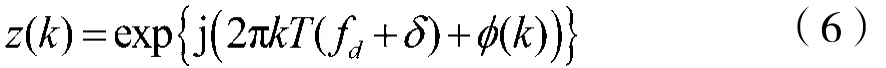
1.3 系统帧结构

本文研究关注于宽带多媒体业务，而DVBS2X协议[14]是常用的宽带多媒体协议，因此本文基于此展开分析。DVB-S2X协议下行物理层帧结构如图3所示。其中，帧头包含SOF（26个符号）和PLS（64个符号）两部分。PLS包含两个信息字段MODCOD和TYPE字段，共7个符号。MODCOD段（5个符号）用于识别复序列前向纠错帧的调制方式和FEC的码率。TYPE段（2个符号）用于识别FEC的长度，并表明有无导频（pilots）。物理层帧中每16个时隙后跟一段导频，每个时隙90个符号，每段导频长度为36个符号，导频和帧头主要用于接收端同步处理。由于不同的调制方式，每帧数据含有的导频段数不同。例如：BPSK调制一帧数据含有11段导频，QPSK调制一帧数据含有5段导频。在辅助数据严重受限的情况下，如何充分利用帧头和导频，使接收端快速高效地实现同步成为该领域的一种挑战。

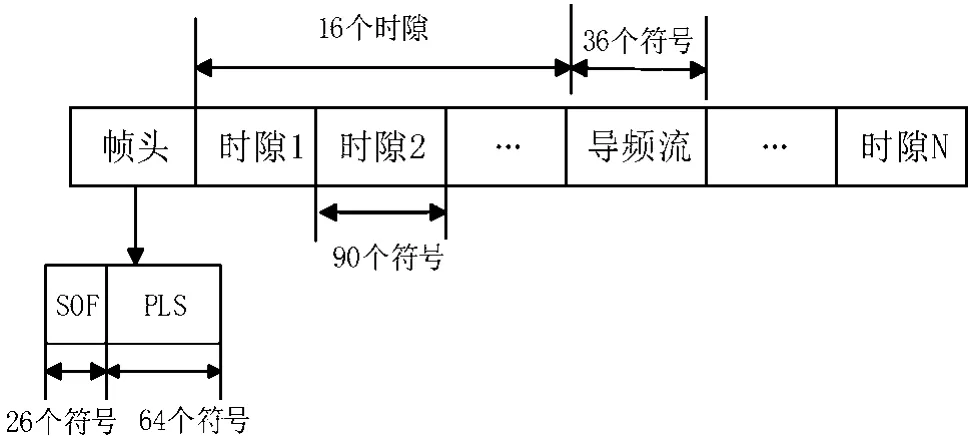
图3 DVB-S2X系统下行物理层帧结构

2 估计器和级联算法的设计

2.1 频率估计器的设计

频率估计器的设计如图4所示。接收端的同步包括定时同步、帧同步和载波同步。载波同步又分为频率捕获和相位跟踪。在帧同步阶段，利用本地序列对SOF和PLS做移位相关。将相关器的输出分成N个长度为L（L取值至少大于1帧数据长度）的搜索窗进行峰值搜索，每段中必定存在一个最大峰值并作为候选。对第一个候选进行PLS解码，推导出下一个SOF和PLS的位置。若推导的位置上SOF和PLS相关性足够强，则帧同步成功；否则，继续对下一个候选进行处理。帧同步后，已知帧头和导频的位置，此时可将其用于辅助载波同步。高动态场景下，多普勒频偏较大，采用一步频率估计算法较难达到相位跟踪所能接受的频偏门限。结合文献[9-12]的思想，将频率估计分两步实现，即粗估计模块得到初始频偏，并通过前馈结构实现频点调整；细估计模块进一步细化估计以获得更高的精度。高动态环境下，多普勒频移具有高阶变化率。细估计模块不仅要估计小频偏，还需估计变化率。

2.2 多级级联算法设计

2.2.1 粗估计算法设计

文献[12]指出，粗估计至少需要20帧才能将频偏从20%减少到10-4。该算法在对接收序列求相关并进行累加得到累加相关函数时，需要多次复数共轭相乘和复数相加，计算复杂度较高。根据辐角的 范 围 -π＜2πLTΔf＜π， 可 知 频 偏 的 范 围 为其中，f为符号速率，L是符号间的间隔。经探索发现，L取值越大，越能平滑噪声的影响，从而算法估计精度越高，但是估计范围也相应减小。因此，可以根据不同场景，选取不同的L值，以获得更高的估计精度。DVB-S2X协议指出，总频偏可能达到符号速率的20%，因此符号间间隔最大可取2。

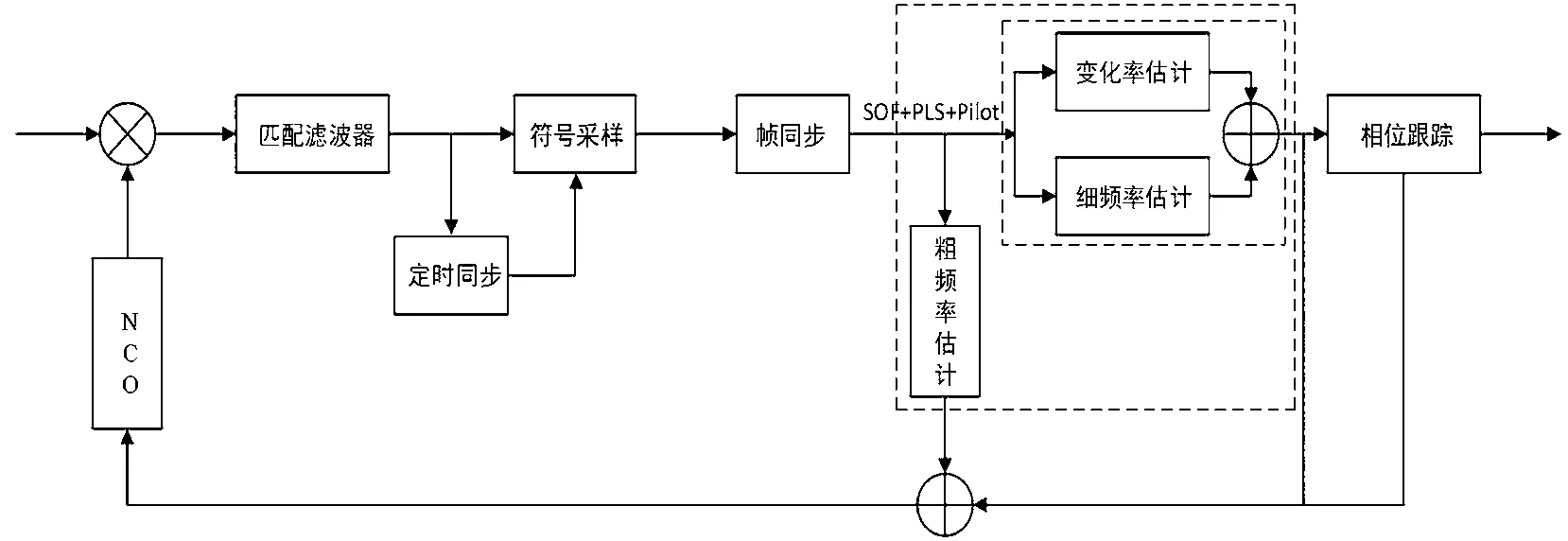
图4 频率估计器的设计

根据L最大取值2的理论分析，可将相邻数据求和并看作一个整体。基于此思想，可对文献[12]中算法进行优化。优化的算法步骤如下：

（1）每两个符号求和且看作一个整体：

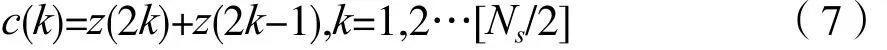
其中，Ns表述每段辅助数据长度，帧头Ns=90，导频Ns=36，[ ]表示取整。

（2）对c(k)序列中各符号求相关，得到相关序列：

（3）将S段相关序列求和，得到累积相关序列：

（4）求解频偏：

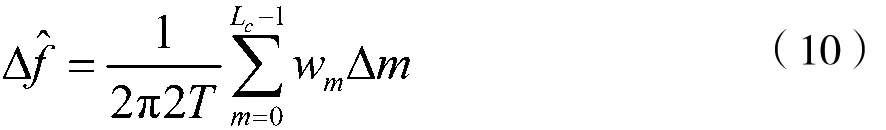
辐角差Δm和权重因子wm分别为：

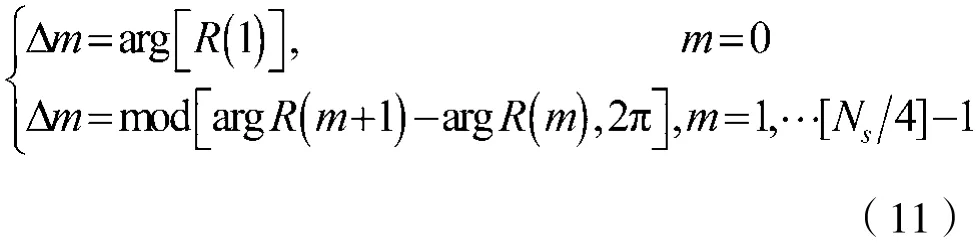
其中，arg[]表示求辐角。

2.2.2 细估计算法设计

经过粗估计与补偿后，无法预知此时的频偏为正值还是负值，而ML估计算法[12]无法高精度对0 Hz以下的频偏进行估计，具有一定的局限性。在工程实现时，需要改进ML估计算法使其与粗估计算法级联，实现频偏收敛。

将每一段导频块求和后看作一个整体，表达式为：

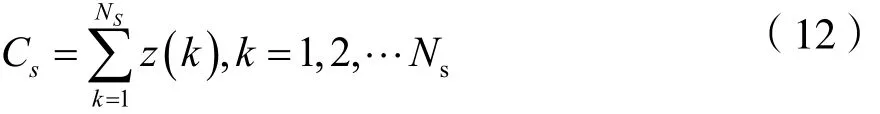
此时，相邻导频段被认为是相邻符号，再利用Kay算法思想，利用相邻符号的相位差求解频偏，因此频偏估计结果为：

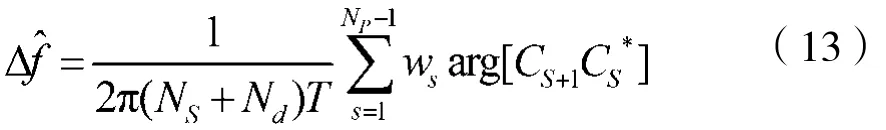
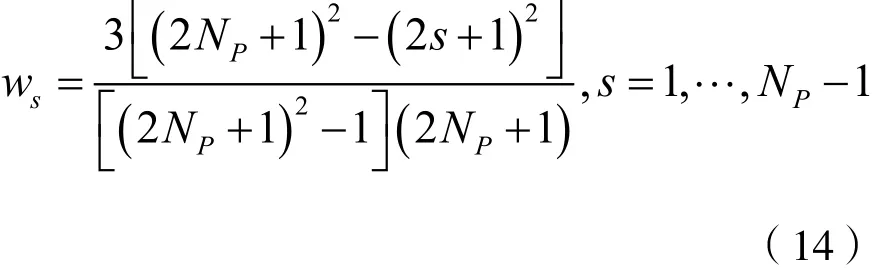
其中，NP表示导频段的段数；Ns表示每段导频的长度，取36；Nd表示数据段长度，取1 440。由于|2πkTΔf|＜π，因此该算法的理论估计范围为与原算法估计范围相比，改进后的算法具有其2倍的估计范围。

3 性能分析

3.1 算法复杂度分析

粗估计算法的优化充分利用符号间的间隔L=2。将文献[12]和本文中粗估计算法的计算复杂度进行对比，结果如表2所示。数据采用不同的调制方式，导频段数不同，设为s段。达到粗估计精度所需要的数据帧数设为n帧。

表2 优化前后的算法复杂度对比

3.2 仿真性能分析

本文仿真参数如表3所示。

DVB-S2X协议中指出，多普勒频移变化率引起的抖动为30 kHz/s，超过表1中给出的不同场景下常用参数的数值。根据计算，传输一帧数据大约需要0.7 ms，在该段时间内变化率引起的频偏大约为21 Hz。因此，本文变化率引起的频偏扰动δ，参考协议标准将其设为0～21的随机数。DVB-S2X协议中还指出，总频偏可能达到符号速率的20%，若符号速率为25 Msps，则频偏为5 MHz。在载波频率为30 GHz时，5 MHz的频偏对应的相对速度为50 000 m/s，同样也超过表1中给出的不同场景下常用参数的数值。通信系统中，不仅会因为相对运动产生频偏，还会因为接收机与发射机的晶振不同等其他原因产生频偏。因此，本文初始频偏设为0.2倍符号速率（即5 MHz），其包含相对运动、硬件等造成的频偏。

表3 仿真参数

图5给出文献[12]和本文中粗估计算法的频偏估计均方根误差对比结果。可以发现，粗估计在0.2倍符号速率频偏下，性能略有下降，但是随着频偏的减小，优化后的性能更佳。

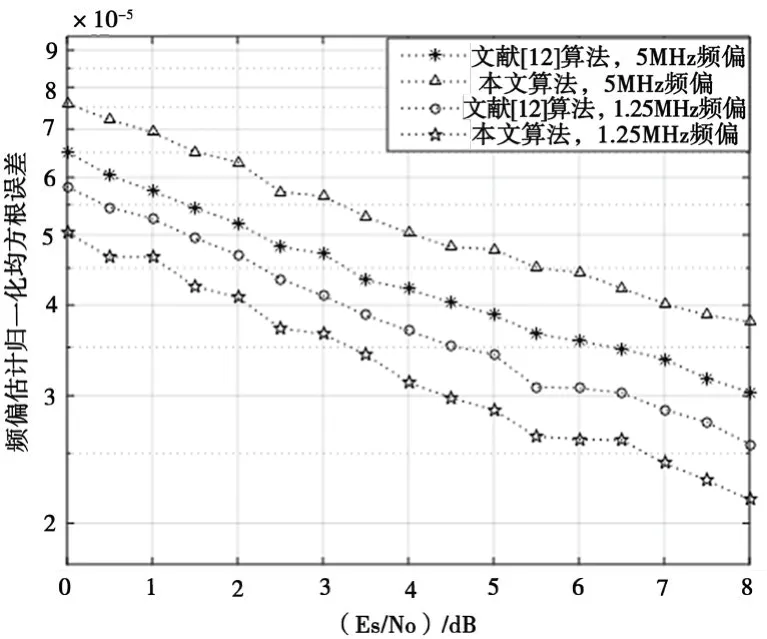
图5 粗估计算法归一化均方根误差对比

图6 为文献[12]和本文中细估计算法仿真对比。1 kHz以上频偏时，本文算法保持原算法精度；0～1 kHz时，与原算法相比，本文算法精度更高。0 Hz以下频偏时，原算法无法对该类频偏进行捕获，而改进后的本文算法在该范围内仍具有较高的精度。相对来说，优化后的细估计算法估计范围扩大2倍。

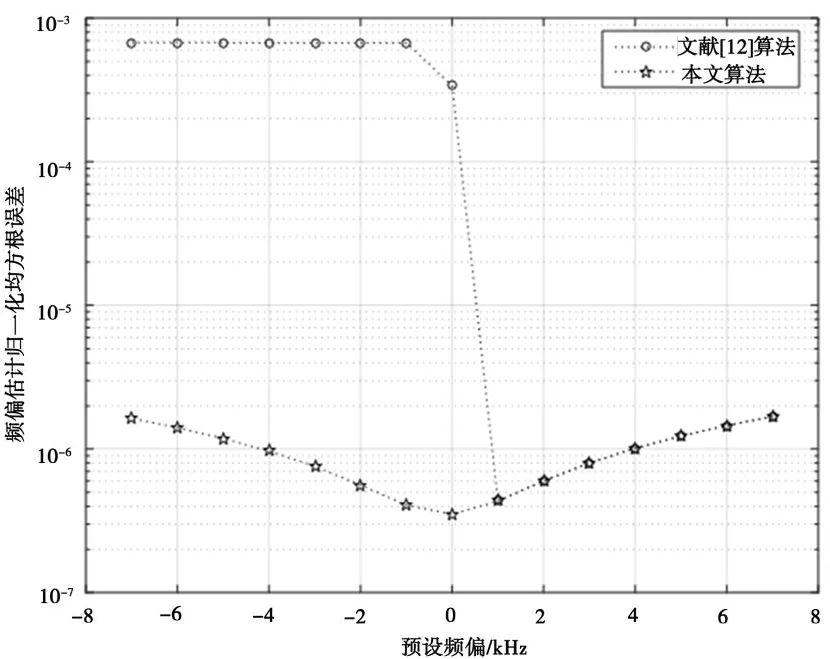
图6 细估计算法归一化均方根误差对比

通过100 000次测试，在0 dB时，频偏为200 Hz（约为符号速率的10-6数量级），链路误码率接近0。图7给出本文粗、细估计级联和文献[12]粗估计和本文细估计级联的仿真曲线图。对比图中曲线，本文算法虽然在0.2倍符号速率频偏时，性能略有下降，但是在0 dB时，频率估计归一化均方根误差约10-7数量级。也就是说，大约偏离设定值20 Hz，远小于译码门限。另外，0.05倍符号速率时，优化后的级联算法性能更优。通过图5和图7可以看出，粗估计采用20帧将频偏从20%降到10-5，再采用细估计将其收敛至10-7。经仿真测试，正常解调译码所能接受的频偏约为10-6。该估计器性能完全满足解调译码的需求。

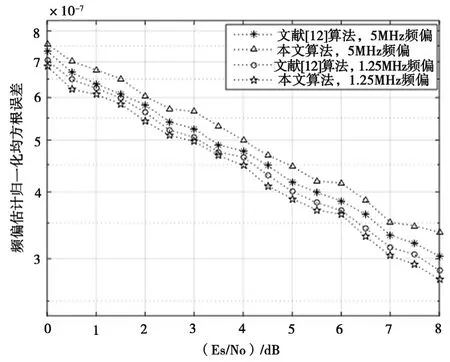
图7 级联算法归一化均方根误差对比

4 结 语

高动态场景下多普勒频移大，采用一步频偏估计算法无法达到解调译码所需精度，故采用粗估计和细估计结合的思想实现频偏收敛。优化前的细估计算法无法实现级联效果，优化后的细估计算法在保持原有精度的条件下，频偏估计范围是优化前的2倍。粗估计算法优化后，与原算法精度相当的同时，计算复杂度为优化前的25%。优化后的级联算法将频偏从20%收敛至10-7，而正常解调译码所能接受的频偏约为10-6，充分说明该估计器具有较高的精度，完全能满足接收端解调译码的需求。