基于带通滤波器频响的电磁干扰信号生成技术*
贺 宇,王 哲,宋 滔,马 谢,郑浩月,武丹丹
(中国电子科技网络信息安全有限公司,四川 成都 610041)
0 引 言
复杂电磁环境下,通信环境中各种类型和体制的电磁信号可能同时存在,如广播、导航、雷达电磁信号以及高功率微波等,并构成了通信环境中的背景电磁干扰信号,对所处其中的电子设备的正常工作带来了安全隐患,影响通信设备的性能发挥和通信质量的好坏[1]。因此,需要研究通信环境中的电磁干扰信号对电子设备的影响效应,以便提高通信电子设备的电磁环境适应能力。目前,广泛采用半实物仿真与验证的方法研究电磁影响效应[2],而半实物仿真的关键是背景电磁干扰信号的生成。
背景电磁干扰信号组成了复杂多变的通信电磁环境,而模拟产生背景电磁干扰信号的方法主要有两种:基于仪器设备的现场采集与回放方法(包括利用真实电子设备或利用信号模拟器的方法)和基于信号处理的计算机模拟生成方法[3]。在实际工程中,利用仪器设备采集实际通信环境中的背景电磁信号的难度较大,多数情况下不实现,且研究过程中往往无法得知通信环境中的背景电磁干扰信号的时域波形(如高功率微波),而只能获得电磁干扰信号的部分频域特征(如工作频段、3 dB带宽、中心频率、场强均值、峰值功率或功率密度等)[4]。因此,工程实践中,采用基于信号处理算法的计算机模拟方式来实现背景电磁信号的生成。但是,根据信号处理的一般条件,若要从频域变换得到时域信号,必须确定频谱的解析式或者知道各个频点对应的幅值数据。所以,获取背景电磁干扰信号的部分频域特征信息还不足以通过傅里叶反变换等频时反演方式得到所期望的时域信号波形[5]。因此,需要一种能够通过有限的频域特征信息,得到一个可以等效模拟所需电磁干扰信号的时域波形的电磁信号生成技术,以便在电磁分析工程研究中应用。
本文基于以上应用背景,提出了一种适用于工程实际的电磁干扰信号生成技术,通过对背景电磁干扰信号频谱的代换,采用基于带通滤波器频率响应的模型建立等效信号,既能较快得到需要的时域信号波形,又能有效满足所需干扰信号的主要频谱特征,能较好地运用于实际的电磁干扰工程分析中。
1 频谱代换
在电磁影响效应的半实物仿真研究过程中,通常只知道干扰信号频谱的部分特征,如工作频段、3 dB带宽、中心频率、场强均值或功率密度等。由以上频域特征,可以描绘出信号频谱的大致形状。一般情况下,是具有类似于如图1所示形状的频谱,工作频段之外的频段,可认为场强幅值为0。
图1中虚线表示未知的曲线形状。实际工程中,可认为在上述虚线区域频谱是单调上升或下降的。通过与带通滤波器技术参数及频响特性进行对比(如图2所示)可发现,以上只知道局部频谱特征的背景电磁信号的频谱分布与带通滤波器的频响特性相似,故可以考虑用一个合适的带通滤波器频响曲线来代换根据局部频谱特征所描述的信号频谱曲线,然后通过综合带通滤波器,设计得到带通滤波器的脉冲响应,从而最终得到一个可以等效模拟所求电磁干扰信号的时域波形。
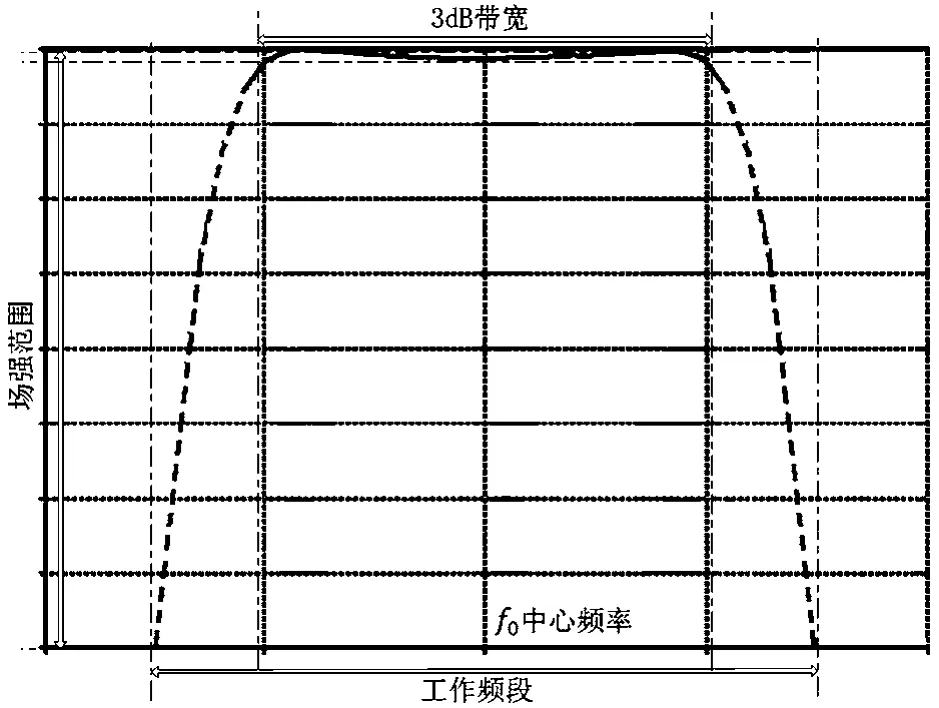
图1 已知部分特征的干扰信号频谱的一般形状
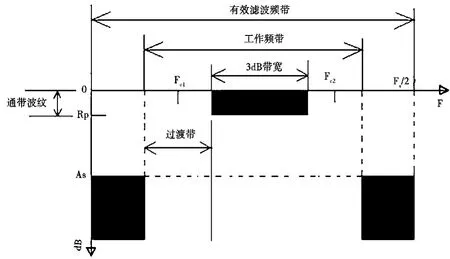
图2 带通滤波器技术参数及频响特性示意
一个已知部分频谱特征的背景电磁干扰信号的频谱可能不是一个如图1所示的单一的上凸曲线形状,而可能是多个单一的上凸曲线的组合,如图3所示的由3个上凸曲线构成的频谱。因此,需要3个中心频率不同的带通滤波器的频响曲线进行代换。
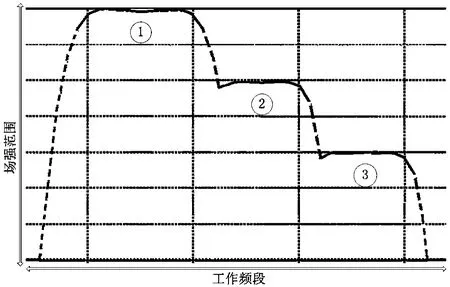
图3 由3个上凸曲线构成的频谱
不失一般性,设一个已知部分频谱特征的背景电磁干扰信号的频谱可以分解成n个如图1所示的单一的上凸曲线的组合,则需要n个中心频率不同的带通滤波器的频响曲线进行频谱代换,通过对各个带通滤波器进行综合,设计得到n个带通滤波器的脉冲响应,最后将n个脉冲响应进行组合,得到一个可以等效模拟所求电磁干扰信号的时域波形。
2 信号生成
基于以上思路,在频谱代换确定的n个带通滤波器频响基础上,确定第i个(1≤i≤n)带通滤波器的频响设计参数如下:阶数为Mi、采样频率为(Fs)i、下过渡带中心频率为(Fc1)i、上过渡带中心频率为(Fc2)i、阻带响应容度为 (δ2)i、阻带衰减为 (As)i、通带响应容度为(δ1)i、通带内纹波为(Rp)i等,并以FIR滤波器为基础进行带通滤波器的综合,其技术参数如图2所示。图中采用的是相对参数坐标,由幅频响应的分贝形式给出如下[6]:
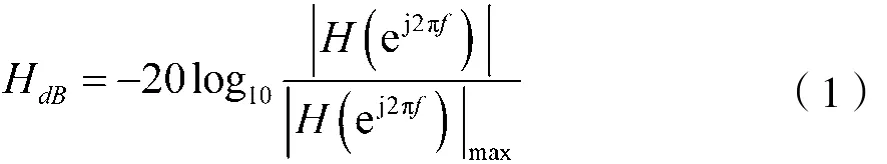
通常,阻带衰减(As)i和通带内纹波(Rp)i有如下关系:
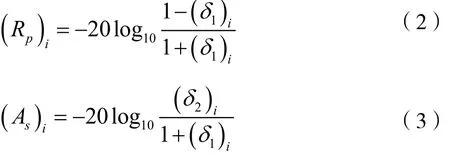
因要求3 dB带宽处于通带内,故通带内纹波(Rp)i取为3 dB,而采样频率(Fs)i与可分解的频谱的有效频带宽度W有效频带有关,关系如下:

另外,下过渡带中心频率(Fc1)i及上过渡带中心频率(Fc2)i,由已知信号的3 dB带宽分布和工作频段决定(参见图2)。因此,由式(2)~式(4)可确定带通滤波器频响的设计参数。而一个理想带通滤波器的脉冲响应可以由两个具有相同的相位响应的理想低通滤波器的幅度响应得到,如图4所示。
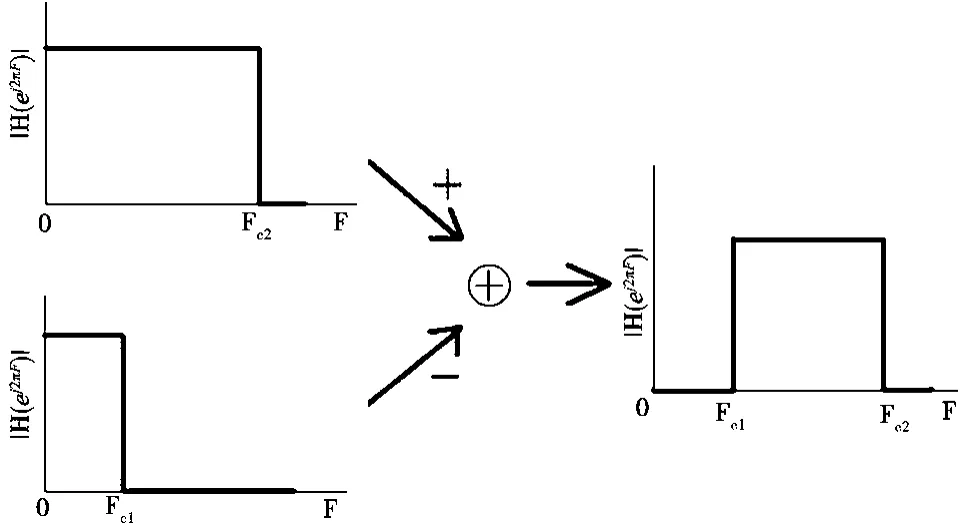
图4 由理想低通滤波器获得理想带通滤波器
将理想带通滤波器的下过渡带中心频率(Fc1)i作为通带较小的一个理想低通滤波器(LPF1)i的通带截止频率,上过渡带中心频率(Fc2)i作为通带较大的一个理想低通滤波器(LPF2)i的通带截止频率,两个理想低通滤波器取相同的阶数Mi,由(LPF2)i的脉冲响应h2(n)i减去(LPF1)i的脉冲响应h1(n)i,得到所需理想带通滤波器的脉冲响应hd(n)i。理想低通滤波器脉冲响应hL(n)及第i个理想带通滤波器的脉冲响应hd(n)i可以表示为:
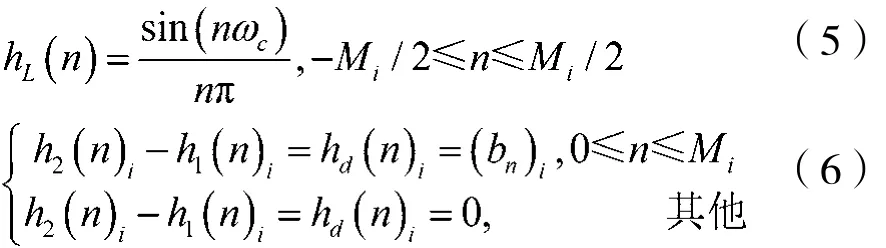
其中ωc是以弧度表示的理想低通滤波器的截止频率。
于是,通过Z变换可得相应的系统函数:
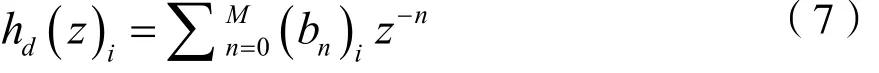
其中(bn)i为第i个带通滤波器系统函数的系数。
由于在滤波器阶数Mi提高后,很难保证得到所需的滤波器频响,为了从hd(n)i得到一个FIR滤波器,必须在hd(n)i两边将它截断,进行这一截断操作的运算称为加窗,对应的运算式称为窗函数,而截断就是hd(n)i和某个窗函数相乘。在得到理想带通滤波器的脉冲响应hd(n)i后,还需要考虑加窗设计,以最终确定脉冲响应h(n)i。通常,可考虑Hamming窗或Blackman窗,其中Blackman窗函数如下:
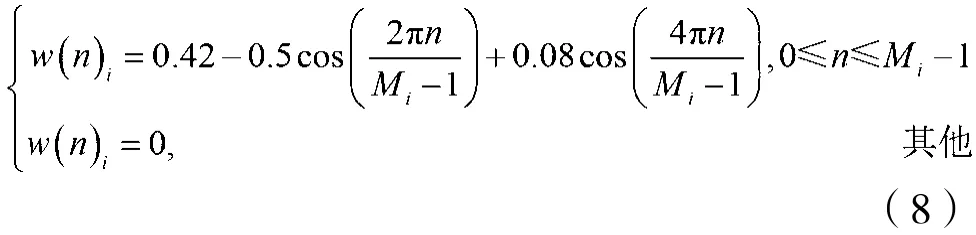
采用Blackman窗后,滤波器阶数Mi可以由式(9)确定:

其中,w上过渡带和w下过渡带是对π进行归一化后的过渡带宽度。
于是,所需滤波器的脉冲响应为:

h(n)i是一个(Mi+1)维的数组。
确定时间序列t(n)i。时间序列t(n)i是从0开始到Ti的一个(Mi+1)维的数组,是与脉冲响应h(n)i数组一一对应的,而时域信号的时间长度Ti与滤波器的阶数Mi及采样频率(Fs)i有关,由式(11)确定:

因此,时间序列t[n]i可由式(12)确定:
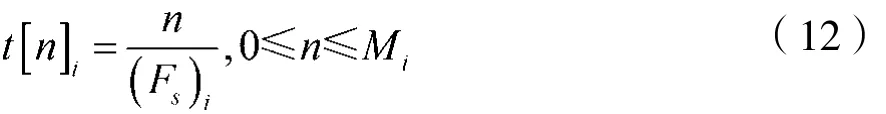
最后进行数据合成。由n=(Fs)i×t[n]i知,带通滤波器的脉冲响应h(n)i也可以写成h((Fs)i×t[n]i)i。因此,可以看出,滤波器脉冲响应h(n)i与时间序列t[n]i存在一一对应关系。将此对应关系作图,将最终得到第i个所需要的时域信号[S]i,此时域信号是一个2×(Mi+1)的矩阵。其后采用离散时间傅里叶变换解算时域信号[S]i的频响特性,使其满足已知的部分频域特征的要求。离散时间傅里叶变换由式(13)~式(15)给出:
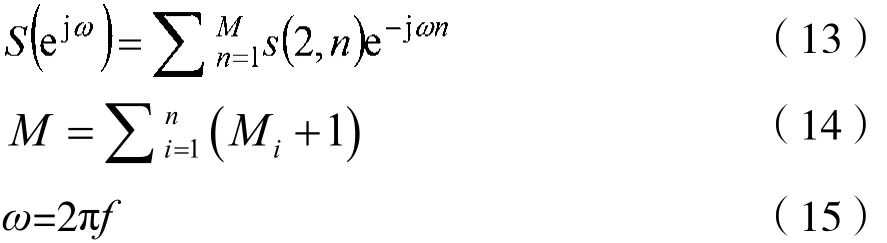
对于需要进行频谱分解的情况(如图3的情况),针对分解得到的单个带通滤波器型频谱,采用以上变换方法分别对其进行频域到时域的反变换,最后将得到的各个时域波形进行线性组合,得到所需的等效时域信号,即将各个反变换得到的n个时域信号合成一个数据,得到所需的时域信号[S],此时域信号是一个的矩阵。
3 应用实例
设已知一个背景电磁干扰信号的部分频域特征如下:
(1)工作频段:0.5~6.8GHz;
(2)3 dB带宽分布:1~3GHz,以及3.2~5.8 GHz;
(3)功率密度均值:1~3GHz内为26.5W/cm2,以及3.2~5.8GHz内为0.265W/cm2
根据以上信息,计算得到两个3 dB带宽对应的中心频率为2 GHz及4.5 GHz,并由式(16)计算得到功率密度对应的电场强度分别为80 dBV/m和60 dBV/m,其中Z0为自由空间波阻抗,SE为功率密度。

另外,工作频段外电场强度可视为小于1 dBV/m。而在工作频段内除去3 dB带宽外的频段,可认为是电场强度从80 dBV/m或60 dBV/m减少至邻近频段电场强度值的过渡段。于是,可知该电磁干扰信号的频谱大致分布如图5所示。
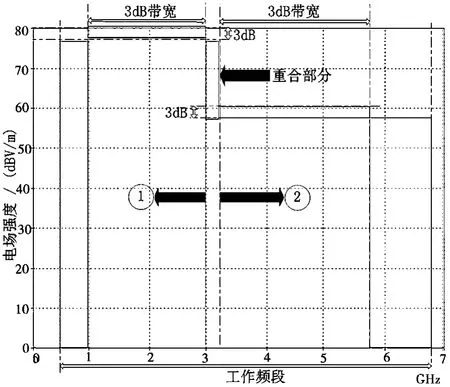
图5 设定电磁干扰信号的频谱大致分布
图5 中阴影部分为频谱曲线分布区域。利用图2所示的带通滤波器技术参数及频响特性,将该设定电磁干扰信号的频谱分解为如图5所示的①和②两部分,并分别用合适的带通滤波器的幅频响应曲线进行频谱代换。
将图5中设定电磁干扰信号的频域参数信息与图2带通滤波器技术参数及频响特性进行对应,可得到用于频谱代换的带通滤波器的幅频响应。对于图5中的①部分频谱,将其3 dB带宽作为所需带通滤波器频响的3 dB带宽,0.5~1 GHz作为所需带通滤波器频响的下过渡带,0~7 GHz作为所需带通滤波器频响的有效滤波频带。另外,从图5可以看出,①部分的右边沿与②部分的左边沿部分重合(如图5中“重合部分”所示),因此用于代换的两个带通滤波器的过渡带必然也相互重叠。为便于研究,设定两个带通滤波器各自的幅频响应曲线中的上过渡带与下过渡带带宽相同,因此选择3~3.5 GHz作为所需带通滤波器频响的上过渡带,同时通带波纹取为3 dB。于是,得到用以进行代换①部分频谱的带通滤波器①的幅频响应曲线,如图6所示。
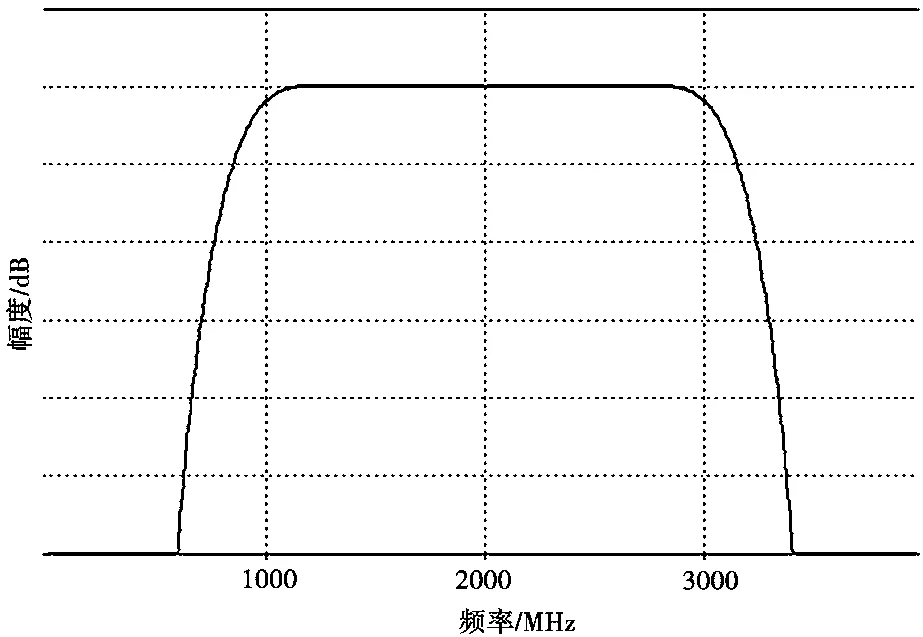
图6 所需带通滤波器①的幅频响应曲线
同理,得到用以进行代换②部分频谱的带通滤波器②的幅频响应曲线,如图7所示。
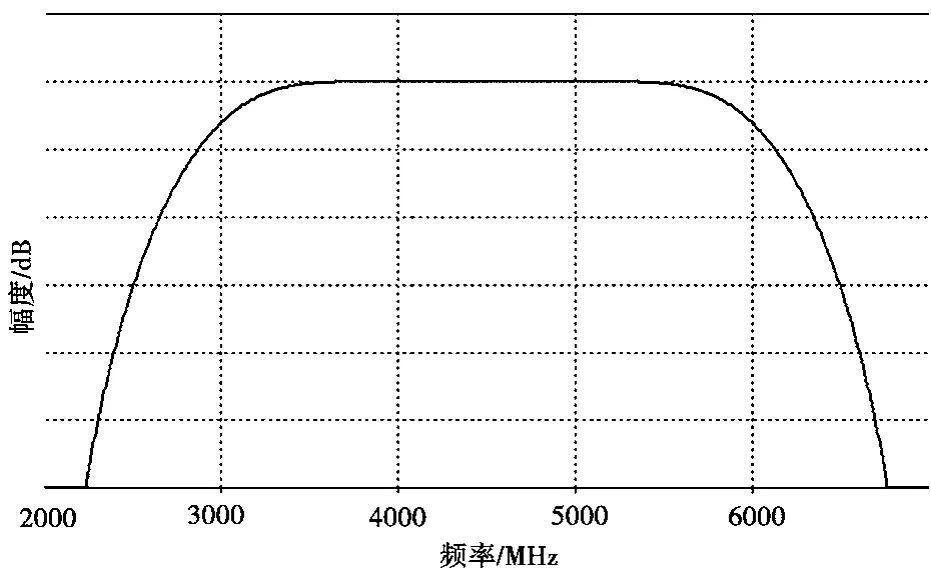
图7 所需带通滤波器②的幅频响应曲线
由于带通滤波器①的中心频率为2 GHz,3 dB通带为1~3 GHz,上过渡带与下过渡带带宽均为0.5 GHz,故可确定其下过渡带中心频率(Fc1)i=750 MHz,上过渡带中心频率(Fc2)i=3.25 GHz。同时,取通带内纹波(Rp)1=3 dB,且由图5可知阻带衰减应取为(As)1=80 dB,则由式(2)、式(3)可计算得到阻带响应容度(δ2)i=0.000 117,通带响应容度(δ1)i=0.17。另外,由图5可知,有效频带宽度为7 GHz,故由式(4)可确定采样频率(Fs)1=14 GHz。
将带通滤波器①的下过渡带中心频率(Fc1)1作为通带较小的一个低通滤波器(LPF1)1的通带截止频率Wc1,采样频率取为(Fs)1=14 GHz,阻带衰减(As)1=80 dB,并采用Blackman窗。又由于有效频带宽度为7 GHz,设W有效宽带对应的弧度为π,则以弧度表示的过渡带宽为W上过渡带=W下过渡带=π/14,由式(9)可以得到阶数M1为155,而通带截止频率以弧度表示为Wc1=3π/28,可得到低通滤波器(LPF1)1的脉冲响应如下:

同样,将上过渡带中心频率(Fc2)i作为通带较大的一个理想低通滤波器(LPF2)1的通带截止频率Wc2,采样频率取为(Fs)1=14 GHz,阻带衰减(As)1=80 dB,并采用Blackman窗。又由于有效频带宽度为7 GHz,设W有效宽带对应的弧度为π,则以弧度表示的过渡带宽为W上过渡带=W下过渡带=π/14。由式(9)可以得到阶数M1为155,而通带截止频率以弧度表示为Wc2=13π/28,可得到低通滤波器(LPF2)1的脉冲响应如下:
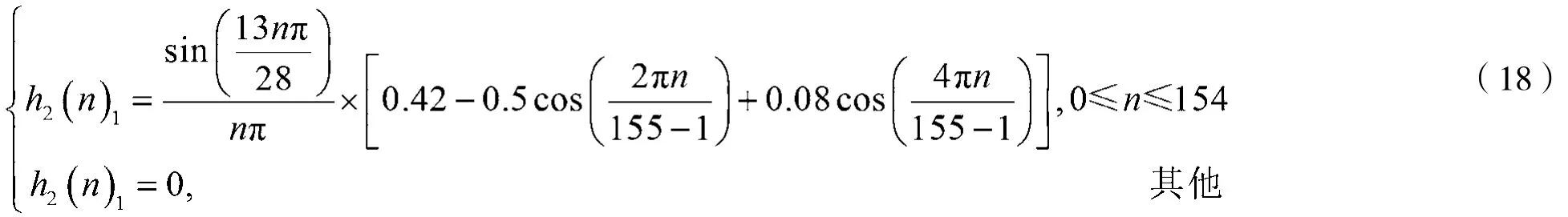
于是,带通滤波器①的脉冲响应h(n)1为:
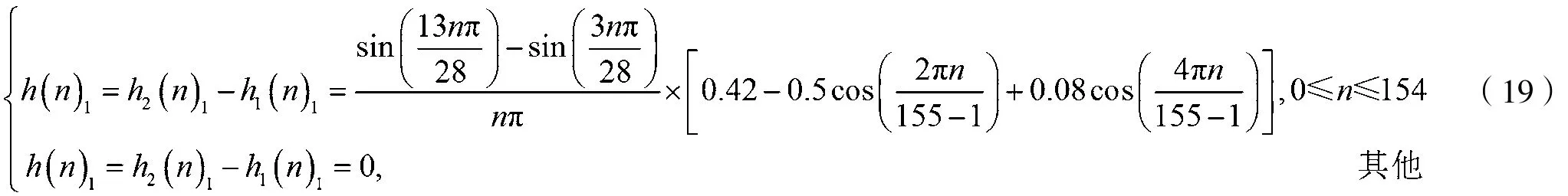
同理,带通滤波器②的脉冲响应h(n)2为:
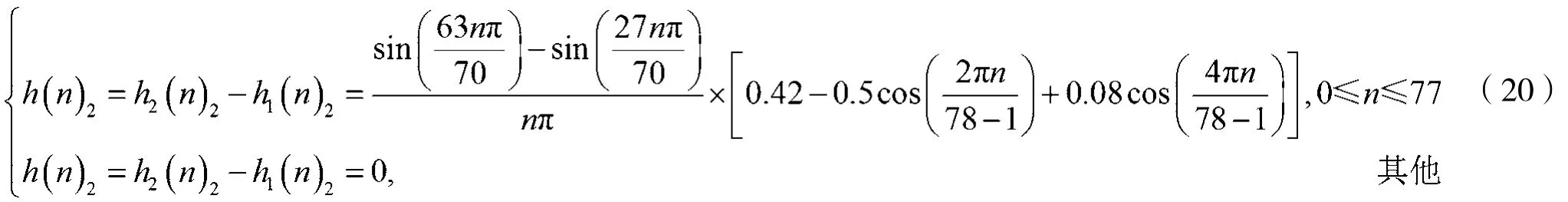
由式(11)得到带通滤波器①的脉冲响应时间序列t[n]1的时间长度为11.07 ns,带通滤波器②的脉冲响应时间序列t[n]2的时间长度为5.57 ns。将长度为11.07 ns的时间序列t[n]1等分成155个时间点,并与脉冲响应h(n)1进行一一对应,得到时域信号序列[S]1;同样,长度为5.57 ns的时间序列t[n]2等分成78个时间点,并与脉冲响应h(n)2进行一一对应,得到时域信号序列[S]2。同时,由图5可知,所求信号的频域①部分的峰值为80 dBV/m,由傅里叶逆变换可知其时域峰值约为4.4 kV/m。又由于②部分比①部分的峰值小20 dB,故②部分对应的时域峰值为①部分的1/10。最终,将[S]1与[S]2进行线性相加,得到所需的等效时域信号序列[S],作图如图8所示。根据式(13)~式(15)对其时域信号进行离散时间傅里叶变换,得到其频谱如图9所示。
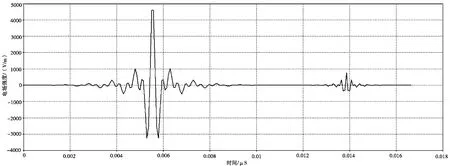
图8 用于代换的等效时域信号波形曲线
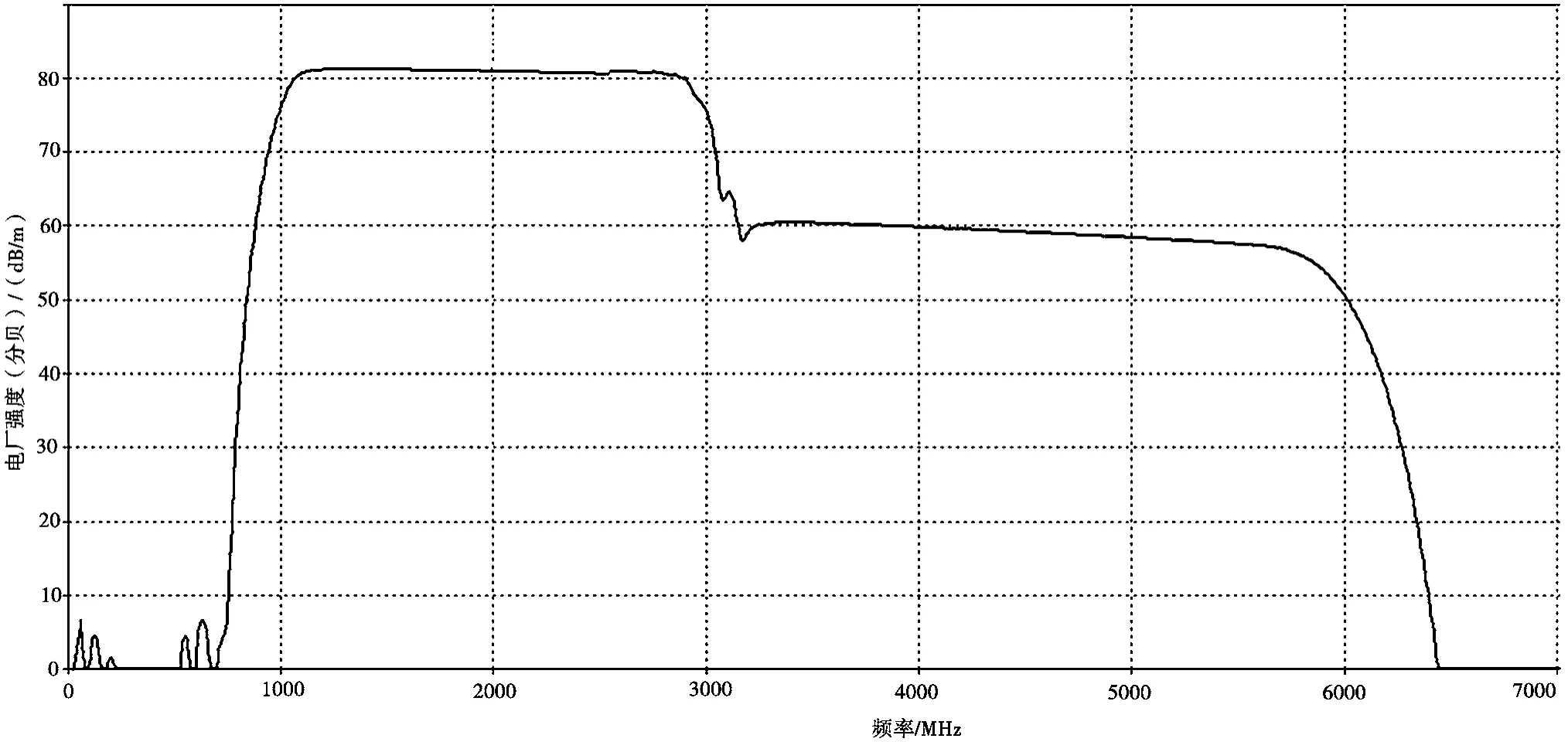
图9 用于代换的等效时域信号的频谱
将图9与设定的已知部分频域特征进行对比可以看出,通过以上基于带通滤波器频率响应的频谱代换得到的预求时域信号的频谱,能够基本满足原设定干扰信号所在频域的工作频段、3 dB带宽分布、以及电场强度均值等频谱特征,且符合图5所示的原设定电磁干扰信号的频谱分布特征。
4 结 语
对于部分频谱特征可以用带通滤波器频率响应来描述的信号,可考虑采用频谱代换的方法得到近似的信号波形,即用带通滤波器的幅频响应替代原信号频谱,并由滤波器的频率响应反推其脉冲响应,再通过实际的时间序列与脉冲响应的对应关系,得到所求信号的时域波形。
该电磁干扰信号生成技术为工程设计人员提供了一种能有效得到满足部分频谱特征要求的电磁干扰信号等效时域波形的方法,可以应用于电磁干扰半实物仿真研究与分析。

