一类具有较大线性复杂度的最优跳频序列集*
刘 方 , 刘 捷
(1.网络空间安全四川省重点实验室,四川 成都 610041;2.中国电子科技网络信息安全有限公司,四川 成都 610041;3.西南交通大学 信息科学与技术学院,四川 成都 610030)
0 引 言
跳频(FH)多址扩频系统具有抗干扰、抗接入的能力,并能做到频谱资源共享。所以,在现代电子战中,跳频通信已显示出巨大的优越性。在跳频多址系统中,载波频率跳变是由一个称为跳频序列的伪随机序列控制频率合成器产生的。跳频序列设计理论目前有两方面的内容,一是寻找跳频序列设计时所受到的理论限;二是设计出达到或接近理论限的跳频序列。跳频序列的线性复杂度可以表征跳频序列被破译的难易程度。线性复杂度越高,表明其抗破译的能力越强。因此,寻找和设计具有低汉明相关、序列集合容量大及具有较大线性复杂度的跳频序列集,是跳频通信系统研究的重要课题之一。
目前,在跳频序列设计的理论界方面,人们已经得到了很多成果,如Lempel- Greenberger界[1]、Peng-Fan界[2]等。在最优跳频序列设计方面,基于组合和代数工具[3-9],人们构造了许多具有最优汉明相关性能的跳频序列集。基于理想自相关特性的p元伪随机序列,构造具有优良汉明相关特性的跳频序列是一种很重要的方法。刘元慧等人[10]基于m序列构造了一类具有新参数的跳频序列集和基于纠错码构造最优跳频序列集[11-13]。
1 基本概念
设一个跳频通信系统具有q个频点,频点集合假设为F={ f1, f2,…, fq}。S是基于频点集F上包含有M个跳频序列的集合,其中每个序列长度为L。对于任意的频点fi、 fj∈F,令:
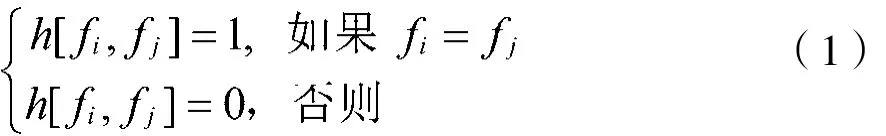
对于跳频序列集S中任意两个序列X={x0,x1,…,xL-1}和Y={y0,y1,…,yL-1},在相对时延为τ时的周期汉明相关函数定义为:
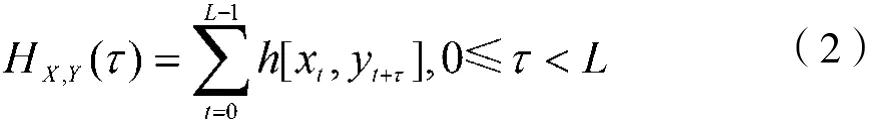
其中,下标t+τ按模L运算。当X=Y时,HX,Y(τ)称 为 汉 明 自 相 关 函 数, 简 记 为 HX(τ); 当X≠Y时,HX,Y(τ)称为汉明互相关函数。
针对跳频序列集S,对任意的两个序列X、Y∈S,下面将分别给出最大汉明自相关函数HX(τ)、最大汉明互相关函数HX,Y(τ)和最大汉明相关函数Hm的定义。
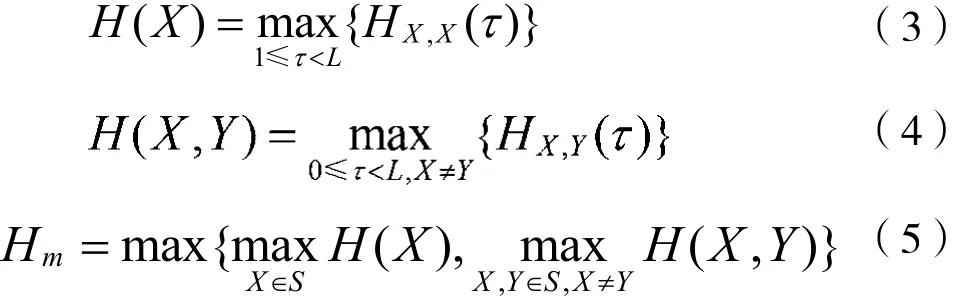
显然,H(X)、H(X,Y)和Hm越小,跳频通信系统的性能越好。因此,跳频序列设计的一个基本要求是使H(X)、H(X,Y)和Hm的值尽可能小。跳频序列设计主要涉及4个参数:频点数目q、序列长度L、序列数目M以及最大汉明相关Hm,而这4个参数受到一些理论界的限制。
对于给定的频点数目、序列长度,单个跳频序列的最大汉明自相关满足下面不等式。
引理1(Lempel-Greenberger界)[1]令X是频点集F上的跳频序列,序列长度为L,那么X的最大汉明自相关值满足:
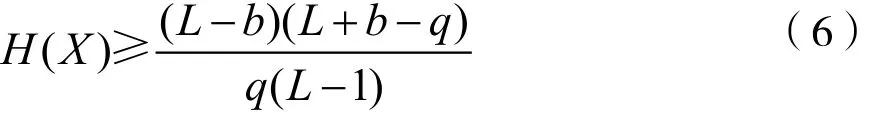
其中,|F|=q,b为L模q的最小非负余数。
在给定频点数目、序列长度和序列个数的条件下,Peng和Fan[2]给出了S个序列集的最大汉明相关值满足的理论界。
引理2(Peng-Fan界) 令S是一个在大小为q的频点集F上的跳频序列集,其序列数目为M,序列长度为L,令 I = [LM] /q ,则有:
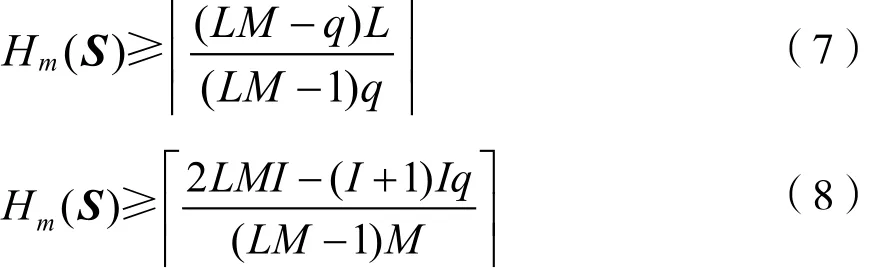
在文献[6]中,Ge、Miao和Yao证明了Peng-Fan界比Lempel-Greenberger界更好。当M=1时,Lempel-Greenberger界是Peng-Fan界的特例;当M=2时,关于H(X,Y),Peng-Fan界要么比Lempel-Greenberger界紧,要么与Lempel-Greenberger界相同。
下面对单个序列和序列集的最优性进行定义。
定义1 如果一个序列X的参数使得式(6)的等式成立,则称X是一个最优的跳频序列;如果一个序列集S的参数使得式(7)或式(8)的等式成立,则称S是最优的跳频序列集。
本文中,使用如下的记号:
(L,q,λ)-FHS表示一个在大小为q的频点集上长度为L、最大汉明自相关值为λ的跳频序列;
(L,M,Λ;q)-FHSS表示在大小为q的频点集上长度为L、序列个数为M、最大汉明相关值为Λ的一个跳频序列集。
2 基于范函数构造跳频序列集
本节提出了一种新的构造方法,所得到的跳频序列集达到了理论界,并具有较大的线性复杂度。
令p是一个奇素数,n、k为一正整数,且k|n,定义:表示从有限域F=Fpn到K=FP迹映射。

范函数NF/K(x)是从有限域F到K的一个映射函数,对任意的x∈F,有:

范函数NF/K(x)具有如下几个特性[14-15]。
性质1:对所有的x、y∈F,NF/K(xy)=NF/K(x)NF/K(y)。
性质2:NF/K(x)是从F到K的满射,F*到K*的满射,其中F*和K*分别表示F和K中的非零元。
性质3:对于任意的a∈K,NF/K(a)=an。
性质4:对于任意的x∈F,NF/K(xp)=NF/K(x)。
令α为Fpn中的本原元,q=pk,n、m、k、s为正整数,且n=(2m+1)k,1≤s≤2m,gcd(s,2m+1)=1。定义 b0=1、bis=(-1)i、bi=b2m+1-i,其中 i=1,2,…,m。令u0=b0/2=(p+1)/2,ui=b2i,其中i=1,2,…,m。定义f(x)为:

容易验证 f(λx)=λf(x),对任意的 λ∈ Fq。
定义如下跳频序列集:

定理1 序列集C为一个(pn-1,p,pn-1;p)跳频序列集。
证明:显然,序列集C中有p个移位不等价序列,频点数为p,序列长度为pn-1。下面证明该序列集的最大汉明相关值为pn-1。
令w表示一个p次单位根,即w=e2πj/p,其中j=。
对于C中任意两个跳频序列ca、cb,a,b∈Fp,其汉明相关函数 Ha,b(τ),0≤ τ<pn-1计算如下:
(1)当 a=b=0,0<τ<pn-1 时,有:
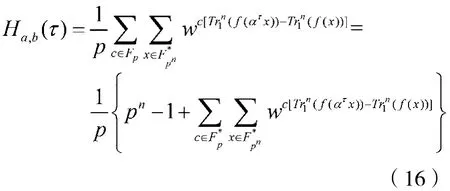
将变量x替换为c-1x,因为:

所以,Ha,b(τ)=pn-1。
(3)对于a≠0,b=0,0≤τ<pn-1时,类似于情况 2,Ha,b(τ)=pn-1。
(4)对于a≠b且ab≠0,0≤τ<pn-1时,有:
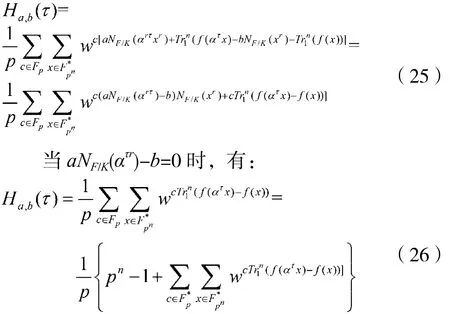
将变量x替换为c-1x,则有:
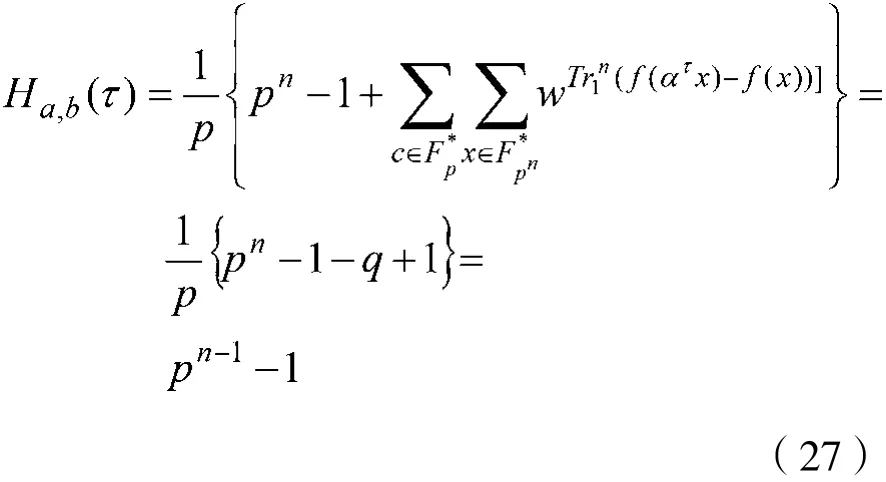
当aNF/K(ατr)-b≠0时,同样对c≠0时进行变量替换x→c-1x,则有:
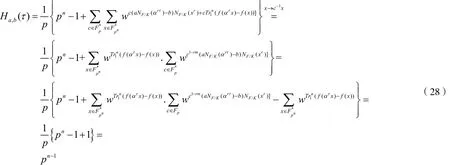
因此,最大汉明相关为pn-1。
(5)对于a=b≠0,0≤τ<pn-1时,有:
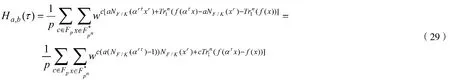
当 0<τ<pn-1 时,因为 gcd(r,p-1),所以 NF/K(ατr)-1 ≠ 0。因此,有:
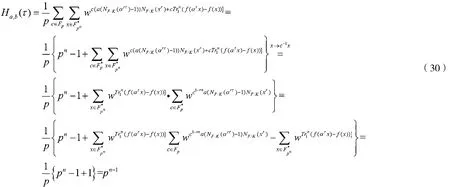
综合以上结果,得到该序列集的最大汉明相关为pn-1。
证明完毕。
定理2 序列集C达到了Peng-Fan界,是一类最优的跳频序列集。

结论得证。
显然序列集C中的序列线性复杂度大于等于(m+1)n。
例1:令q=5、m=1、k=1、n=3、s=2,则f(x)=3x-x13,那么得到序列集C={c0,c1,c2,c3,c4}为:
c0={1,1,4,1,0,1,0,0,4,2,4,2,2,4,1,1,3,1,2,2,0,1,3,4,1,1,0,2,3,1,0,2,2,3,2,0,2,0,0,3,4,3,4,4,3,2,2,1,2,4,4,0,2,1,3,2,2,0,4,1,2,0,4,4,1,4,0,4,0,0,1,3,1,3,3,1,4,4,2,4,3,3,0,4,2,1,4,4,0,3,2,4,0,3,3,2,3,0,3,0,0,2,1,2,1,1,2,3,3,4,3,1,1,0,3,4,2,3,3,0,1,4,3,0};
c1={2,0,0,0,1,0,1,4,0,1,0,1,3,3,2,0,4,0,3,1,1,0,4,3,2,0,1,1,4,0,1,1,3,2,3,4,3,4,1,2,0,2,0,3,4,1,3,0,3,3,0,4,3,0,4,1,3,4,0,0,3,4,0,3,2,3,1,3,1,4,2,2,2,2,4,0,0,3,3,3,4,2,1,3,3,0,0,3,1,2,3,3,1,2,4,1,4,4,4,4,1,1,2,1,2,0,3,2,4,3,4,0,2,4,4,3,3,2,4,4,2,3,4,4};
c2={3,4,1,4,2,4,2,3,1,0,1,0,4,2,3,4,0,4,4,0,2,4,0,2,3,4,2,0,0,4,2,0,4,1,4,3,4,3,2,1,1,1,1,2,0,0,4,4,4,2,1,3,4,4,0,0,4,3,1,4,4,3,1,2,3,2,2,2,2,3,3,1,3,1,0,4,1,2,4,2,0,1,2,2,4,4,1,2,2,1,4,2,2,1,0,0,0,3,0,3,2,0,3,0,3,4,4,1,0,2,0,4,3,3,0,2,4,1,0,3,3,2,0,3};
c3={4,3,2,3,3,3,3,2,2,4,2,4,0,1,4,3,1,3,0,4,3,3,1,1,4,3,3,4,1,3,3,4,0,0,0,2,0,2,3,0,2,0,2,1,1,4,0,3,0,1,2,2,0,3,1,4,0,2,2,3,0,2,2,1,4,1,3,1,3,2,4,0,4,0,1,3,2,1,0,1,1,0,3,1,0,3,2,1,3,0,0,1,3,0,1,4,1,2,1,2,3,4,4,4,4,3,0,0,1,1,1,3,4,2,1,1,0,0,1,2,4,1,1,2};
c4={0,2,3,2,4,2,4,1,3,3,3,3,1,0,0,2,2,2,1,3,4,2,2,0,0,2,4,3,2,2,4,3,1,4,1,1,1,1,4,4,3,4,3,0,2,3,1,2,1,0,3,1,1,2,2,3,1,1,3,2,1,1,3,0,0,0,4,0,4,1,0,4,0,4,2,2,3,0,1,0,2,4,4,0,1,2,3,0,4,4,1,0,4,4,2,3,2,1,2,1,4,3,0,3,0,2,1,4,2,0,2,2,0,1,2,0,1,4,2,1,0,0,2,1}。
可以计算得到H(c0)=24,H(ci)=25,其中1 ≤ i<5。 针 对 0 ≤ i≠ j<5,H(ci,cj)=25。 容 易 验证c0关于Lempel-Greenberger界是一个最优的(124,5,24)-FHS;而对于i=1,2,3,4,ci关于Lempel-Greenberger界是几乎最优的(124,5,25)-FHS。通过简单的验证,C关于Peng-Fan界是一个最优的(124,5,25;5)-FHSS。c0的线性复杂度为6,其他4个序列的线性复杂度为7。
需要注意,当f(x)=x时,序列集C即为参考文献[8]第IV节所得到的序列集。C中的每个序列的线性复杂度为n。如果采用其他的f(x)函数,那么能得到具有更大线性复杂度的最优跳频序列集。
3 结 语
本文基于范函数构造了一类跳频序列集,通过计算证明了该类跳频序列的汉明相关性能满足Peng-Fan界,是一类具有最优汉明特性的跳频序列集。同时,本文得到的跳频序列线性复杂度大于等于(m+1)n,相较已有序列具有较大的线性复杂度,因此这些跳频序列在军事通信系统中具有很好的应用前景。

