基于乘客舒适度的悬挂式单轨平面圆曲线参数研究

张学军,余浩伟,谢 毅,梁 玉,寇峻瑜

(1.中车青岛四方机车车辆股份有限公司,青岛 610031； 2.中铁二院工程集团有限责任公司,成都 610031)

引言

悬挂式单轨，国内又称“空轨”、“空铁”，是我国近年来兴起的一种新型轨道交通制式，由于具有运营安全可靠、线路适应性强、建设周期短、环境友好、视觉效果好、建设成本低等鲜明的特点，自2011年以来在国内得到了快速发展[1-4]。

线路平面设计参数是决定线路平面方案的重要控制参数，直接影响建设成本、运营安全、维修工作量、乘客舒适度等。从利于线路敷设、降低工程量、减小征地拆迁等角度考虑，宜采用较小的曲线半径；从减小轨道梁加工制造难度、利于运营维护和节约能源、提高乘客舒适度角度考虑，宜采用较大的曲线半径。曲线半径的合理取值，应根据以上因素综合考虑。

本文运用行驶动力学[5]理论，从乘客舒适度角度出发，就悬挂式单轨线路平面最小曲线半径、圆曲线长度取值进行计算研究。

1 悬挂式单轨基本原理

悬挂式单轨交通采用轨道在上、车辆在下的特殊结构形式，可形象通俗的理解为“超大型缆车”，通常采用高架桥梁结构，车辆悬挂在轨道梁下方空间行驶，由车辆、轨道梁桥、车站、供电系统、通信信号系统等组成。轨道梁一般采用下部开口的箱形钢梁，墩柱可采用混凝土结构或钢管结构，双线地段一般采用“Y”形桥墩，特殊地段可采用门架形式，单线地段一般采用“倒L”形。道岔为箱形梁内的可动轨结构，通过可动轨的水平移动来实现列车行驶方向的改变[6-7]。

车辆可分为转向架、悬挂装置和车体三部分，与其他轮轨交通区别较大的在于其转向架结构以及悬挂装置。两轴转向架置于轨道梁内部，沿着箱形梁内的轨道面运行，除走行轮外，转向架上还设有单独的导向轮，使得车辆可方便地通过较小的曲线半径。车体与转向架之间为铰接结构，但设置有抗横摆减震器，用以平衡车辆通过曲线时的离心力，消减车辆通过曲线后的横向摆动，抗横摆减震器作用力大小、车体横向摆动姿态是一种动态非线性变化过程，与线路平面设计参数、平面线形等关系密切。如图1所示。

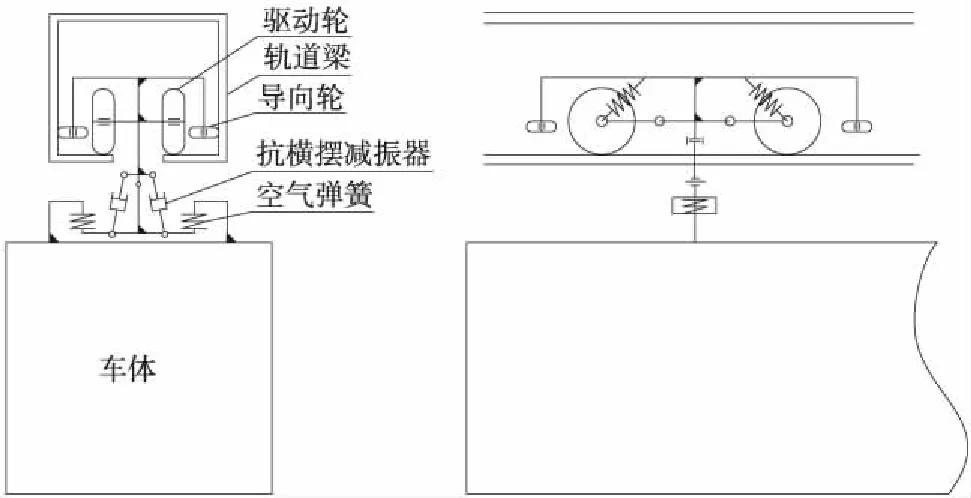
图1 悬挂式单轨车辆结构

目前，国内研发的悬挂式单轨车辆多以德国H-bar车辆为原型，理论上可适应30 m的最小曲线半径、10%的最大坡度。

2 计算方法

作用车体的力主要有车辆重力和中心销拉力。车辆在平面上作曲线运动时，会产生离心加速度，在完全无约束的条件下，车体会在离心加速度的作用下发生一定角度的偏转，当重力在向心方向的分量与离心力相等时，车体即达到平衡状态。实际情况下，由于车体与转向架之间的连接并非完全无约束，会有减震阻尼的存在。同时，车辆生产厂商一般也会对车体的最大允许偏转角进行限定，使得车体的实际偏转角无法完全达到根据向心力所需的计算偏转角，会在产生未被平衡离心加速度。线路设计中通常用限制偏转角和未被平衡离心加速度来保证乘客舒适度。悬挂式单轨车辆受力见图2。

图2 悬挂式单轨车辆受力简图

设车体偏转角为α，纵坡为β，未被平衡离心加速度为aq，平面曲线半径为RH，竖曲线半径为RV，则

(1)

其中

(2)

轨道交通纵坡一般较小，纵坡对于平面曲线半径的影响可以基本忽略不计，令β=0，则算式可简化为

(3)

由式(3)可知，当速度一定时，允许的最小曲线半径直接由车辆最大允许偏转角和允许的最大未被平衡离心加速度决定，且呈反比例关系。即偏转角越大，曲线半径越小；未被平衡离心加速度越大，曲线半径越小。

3 最小平面曲线半径

3.1 最大偏转角

在传统轮轨铁路中，偏转角通常用超高表示。最大超高应保证列车不致倾覆，保证旅客站立或行走时不致失稳；最大欠超高应考虑钢轨磨耗及旅客舒适度要求[8-13]。根据铁道科学研究院1980年的试验研究，当轮轨列车停在超高为200 mm及以上的曲线上时，部分旅客会感到站立不稳，行走困难且有头晕不适之感，故轮轨系统实设超高允许值不应大于200 mm[14]，换算成偏转角表示即为7.7°。国内相关规范对于最大超高值的规定虽不尽相同，但均在120～180 mm(换算成偏转角为4.574°～6.843°)范围内[15]，变化幅度不大，且均处于铁科院试验得出的范围之内。

对于悬挂单轨车辆而言，由于采用的是被动摆的悬挂结构，当车辆停车或低速行驶时，车体在重力的作用下会自动减小偏转角，故不存在传统轮轨由于轨道设置了超高导致的站立不稳或行走困难的现象，但也并非意味着悬挂式单轨可不限制最大偏转角。一方面，会对车辆导向机构、悬挂装置等的制造提出更高的要求；另一方面，过大的偏转角会增大限界范围(图3)和线间距，会造成工程量以及投资的增加[16-19]。此外，偏转角大小还与振动衰减周期、最大侧向摆动速度等相关。

图3 悬挂式单轨限界示意

根据以上分析可以，传统轮轨确定最大超高的方法并不适用于悬挂式单轨，具体方法尚有待进一步研究探讨。结合德国、日本应用情况，本文建议悬挂式单轨最大偏转角暂取目前国内轮轨的最大限制，即6.843°。

3.2 最大未被平衡离心加速度

未被平衡的离心加速度大小是影响乘客舒适度的主要因素之一。在一定的范围内，允许适当的未被平衡的离心加速度存在，可在相同运行速度的条件下降低曲线半径标准，或同样的曲线半径标准可以提高运行速度。

根据国内外在铁路上进行的相关试验和ISO2631标准规定，乘客能承受的被平衡的离心加速度限值一般都处于0.3～1.2 m/s2区间内，且人体可忍受的连续作用时间与未被平衡的离心加速度大小成反比，随着离心加速度的提高，人体能够连续忍受的时间不断缩短。传统轮轨铁路对于未被平衡离心加速度一般以欠超高来表示，欠超高值在34.5～110 mm(换算成离心加速度为0.4～0.72 m/s2)之间，说明随着应用环境的不同，人体可承受的未被平衡离心加速度存在较大的变化幅度。经过对相关规范的统计分析，城市轨道交通由于主要以站立乘客为主，乘客重心高，其相应允许的未被平衡离心加速度取值均较铁路小。

悬挂式单轨的未被平衡离心加速度，是由于车辆在通过曲线时的车体偏角受到约束而产生的，与其他制式相比，悬挂式单轨由于距离地面较高，且车体以下无可遮挡的建筑物，乘客对于未被平衡离心加速度的感觉更加敏感，并存在一定的主观感觉放大效应，即相同的未被平衡离心加速度下，人对于舒适度的主观感觉更差，需要从严控制未被平衡离心加速度。另一方面，为充分发挥悬挂式单轨的优势，减少土建工程和拆迁量，其多沿既有道路两侧或者中央分隔带敷设，需要有更小的曲线半径以适应城市道路的既有线形。建议悬挂式单轨允许的未被平衡离心加速度按一般和困难两档进行选用，当一般情况下选用目前国内城市轨道交通制式的最低值0.4 m/s2，困难情况下选用0.8 m/s2。

3.3 最小平面曲线半径

当最大偏转角取6.843°，最大未被平衡离心加速度取0.4 m/s2或0.8 m/s2时，根据式(3)可计算得出悬挂式单轨最大速度与半径之间的关系。

一般：

(4)

困难：

(5)

基于舒适度要求的不同速度下的平面曲线最小半径如表1所示。

表1 平面曲线最小半径 m

其余半径可按照式(4)和式(5)进行计算，并取为10 m的整数倍。

4 最小圆曲线长度

缓和曲线起、终点处的曲率变化不连续，当列车通过时，会对列车产生一定的冲击作用，从而产生振动。从满足乘客舒适度角度出发，圆曲线最小长度必须满足列车通过时，前后两次振动不叠加，即车辆在前一个缓和曲线产生的振动衰减后，再进入第二个缓和曲线。夹直线和圆曲线的最小长度根据振动衰减要求确定。

圆曲线最小长度L与衰减周期数、振动周期T和速度V的关系可按式(6)进行计算。

(6)

衰减周期数和振动周期主要由车辆的悬挂参数决定。衰减周期数日本地铁取值为1.5～2.5，国内磁浮研究成果为0.5～1.0，铁路设计规范为1.5～2.0。振动周期日本地铁取值为1.2～1.6 s，铁路设计规范为1 s。悬挂式单轨车辆的悬挂结构和参数与传统轮轨车辆存在较大区别，其取值远大于传统轮轨车辆。根据文献[20]的研究成果，悬挂式单轨的振动周期为4～5 s，衰减周期数为2～3次，经2～3个周期衰减后的振动幅值为振动最大峰值的10%～15%。据此计算，悬挂式单轨最小圆曲线长度宜为2V～4V，为传统轮轨铁路最小圆曲线长度0.5V的4～8倍，远大于传统轮轨车辆。

5 结论

(1)运用行驶动力学理论，基于乘客舒适度计算了最小平面曲线半径和最小圆曲线长度，可供后续研究和标准制定时参考。

(2)根据传统轮轨铁路经验，车辆最大偏转角一般情况下不宜大于6.843°，最大未被平衡离心加速度可视具体线路情况取0.4 m/s2或0.8 m/s2，具体可结合车辆参数和线路试验结果进一步研究确定。

(3)悬挂式单轨车辆的悬挂结构和参数与传统轮轨车辆存在较大区别，最小圆曲线长度应不小于2V，是传统轮轨铁路的4倍，在线路设计中应予以重视。

(4)后续可在本文研究的基础上，通过建立车辆-线路耦合动力学模型，利用车线耦合动力学理论对乘坐舒适性、车线动力响应、车辆性能与线路参数之间的匹配关系等进行研究，并结合建设成本、运营维修等因素，合理确定线路参数取值。