沪铜现货与期货协整分析

(同济大学经济与管理学院 上海 200000)

一、理论依据

现货价格和期货价格之间的关系可以通过持有成本理论来表述。商品持有者可能会认为持有商品比持有期货合约能提供更多便利。一般而言，持有实物资产可以确保工厂的正常运行，并且从商品的暂时局部短缺中盈利，而持有一个期货合约并不能做这一点。由于持有商品而带来的好处被称为是商品的便利收益率。

在无套利情况下，期货合约的价格可以按照其公允价格定价，期货市场与相应的现货市场间不存在任何的套利机会，期货价格与现货之间的价格关系可以表述为：

Ft,T=Ste(r+u-y)(T-t)

(1)

Ft,T是到期日为T的期货合约在t时刻的价格，St是现货价格，r是无风险利率，u是单位商品的贮存成本占即期价格的比例，y是便利收益率。如果Ft,T>Ste(r+u-y)(T-t)，那么套利者可以通过在现货市场做多并同时在期货市场做空来获利。

二、数据选取

本文选取沪铜现货和沪铜期货，分析其协整关系。

上述公式(1)可转化为

ft=st+(r-u-y)(T-t)

(2)

其中ft=ln(Ft,T)，st=lnSt

出于减小(r+u-y)(T-t)项的影响，这里选取了1995/4/17-2017/7/13的沪铜现货和沪铜近月连续合约的对数收盘价。

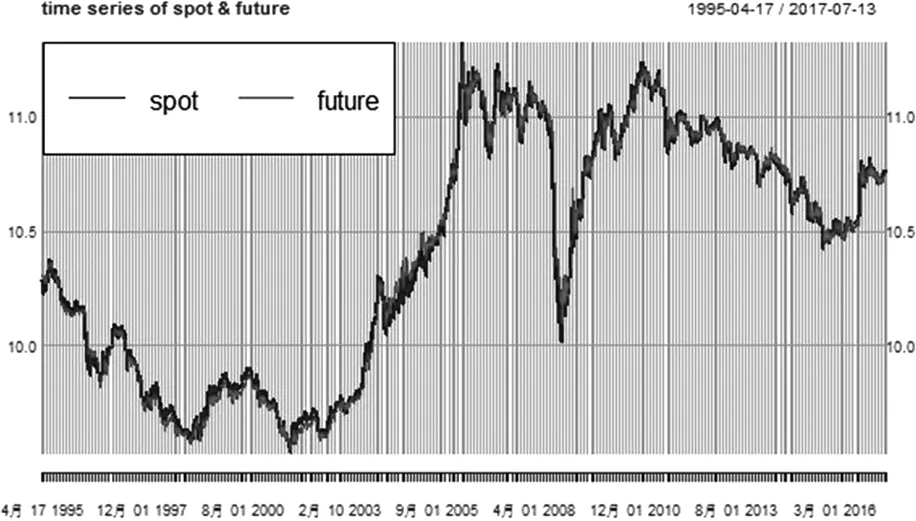
图1 沪铜现货价格和期货价格走势

从上图中可以看出，沪铜现货价格和期货价格走势基本吻合，存在着明显的长期均衡关系。

三、单位根检验

我们先对现货对数收盘价st和期货对数收盘价ft做ADF检定，置信水平选择5%，结果发现st和ft均是非平稳序列。接着继续对st和ft的一阶差分Δst和Δft做ADF检验，结果发现Δst和Δft均为平稳序列，所以得出结论：st和ft为I(1)变量。

表1 ADF单位根检定结果

注：表中为P值，***，**，*分别代表置信水平1%，5%，10%

四、构建VECM模型

按照SC标准构建最佳阶数的VECM模型VECM(3)

(3)

(4)

表2 显示了Engle—Granger和Johanson MLE的协整向量

从表2可知非均衡误差ECTt-1=st-1-ft-1，即非均衡误差为沪铜现货和期货对数价格的基差。

如果我们想知道现货价格和期货价格之间是否存在长期均衡关系，我们就要检验st和ft是否存在协整关系。表3显示了结果。

表3 Engle-Granger检验结果

注：***，**，*分别代表置信水平1%，5%，10%

结果表明：在5%的置信水平下，现货和期货之间存在着现货向期货的单向协整，在其他变量保持不变的情况下，现货价格相对于期货价格超出其均衡关系1%，下一期现货价格就平均下降0.018%。这表明非均衡误差对现货价格的影响尤为显著。所以短期内如果沪铜现货和期货价格偏离其均衡关系，我们可以根据期货价格来预判现货的走势。

五、格兰杰因果检验

为了检定沪铜期货价格和现货价格之间的因果关系，我们进行了格兰杰因果检验。结果如表4所示。

表4 格兰杰因果关系检验结果

注：***，**，*分别代表置信水平1%，5%，10%

结果表明：在5%的置信水平下，沪铜现货价格不是期货价格的格兰杰原因的原假设不被拒绝，而沪铜期货价格不是现货价格格兰杰原因的原假设被拒绝。所以在滞后3阶的情况下，沪铜期货价格是现货价格的格兰杰原因。

六、构建TVECM模型

前面的VECM模型并没有考虑到交易成本，而投资者在市场上的实际操作时是存在着交易成本的，对于套利者来说，只有期货和现货之间的价格偏差(即基差的绝对值)大于交易成本时，才会发生套利行为，因此现货价格和期货价格之间的长期均衡关系对于现货价格和期货价格的修正会表现出时变性和非线性特征。

基于以上设定，这里的TVECM模型如下：

(5)

(6)

这里的Dt-1是虚拟变量，当存在套利机会时取1，当不存在套利机会时取0，δ1和δ2表示不存在套利机会时的误差修正系数，δ3和δ4表示存在套利机会时的不同误差修正部分；所以当存在套利机会时，现货市场上的误差修正系数为δ1+δ3，期货市场上误差修正系数为δ2+δ4。我们设定两个门限值，门限值估计结果为-0.0094和-0.0463，参数估计结果如表5所示

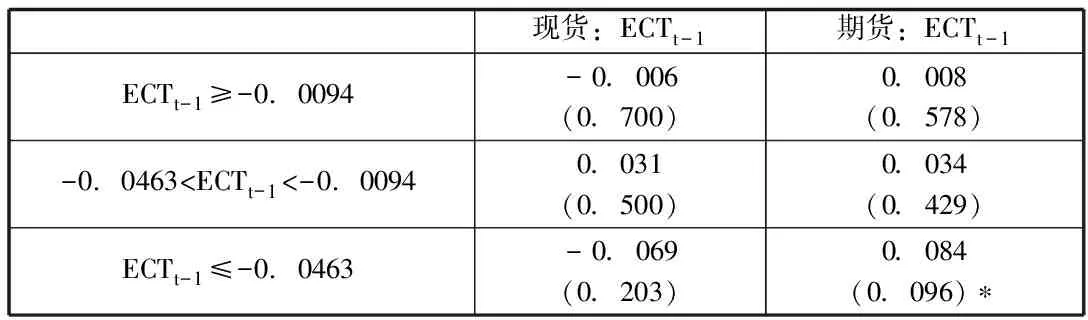
表5 TVECM模型估计结果

注：括号内为P值，***，**，*分别代表置信水平1%，5%，10%

结果表明：在5%的置信水平下，期现货价格不存在显著的协整关系。但是在10%的置信水平下，当ECTt-1≤-0.0463时，沪铜现货和期货之间存在着期货向现货的单向协整，现货价格相对于期货价格超出其均衡关系1%，下一期期货价格就平均上升0.084%。短期内当沪铜现货期货对数价格的基差小于等于-0.0463时，可以根据现货的价格判断期货价格的走势。