面向需求和供应不确定的供应链优化模型研究

(河北工业大学 天津 300401)

一、引言

当今世界，激烈的市场竞争和客户偏好的迅速变化，以及技术和全球化的快速发展，迫使组织作为供应链的成员而不是作为个体企业运营。供应链上下游成员之间的联系更加紧密，信息共享更加频繁。 邵鲁生[1]等人研究了当多阶段、单产品的三级供应网络节点失效时引起供应中断时，提出了重新优化供应计划、启用备选供应商、修复失效供应商的综合应急策略；汪传旭等[2]人研究了有两个供应商和两个零售商组成的二级供应链系统，供应中断用不同情境下的概率来表示，从零售商的角度如何建立最优决策模型，对通过改变中断概率进行灵敏度分析，验证模型的有效性和实用性；李新军等[3]人研究中断状态下，备份供应商的订货决策问题。邓卫华等[4]人在需求和供应均不确定的情况下建立期望收益模型，运用博弈论的知识，证实在不确定条件下的存在双方期望收益的最优解。结果显示，当需求不确定性较大时，零售商应拒绝双方信息共享，供应商的信息推测能力较强时，零售商应接受双方信息共享；彭红军等[5]研究了原材料生产、产成品生产以及市场需求不确定下供应链风险共担契约与模型。构建了风险共担协调契约与模型，最后进行了算例分析。

本文考虑由I个供应商、J个配送中心和M个零售商组成的三级供应链网络。主要考虑供应过程的中断，比如生产设备连接的中断，供应商中断，运输过程的中断等。供应链主要会遇到以下两种不同的风险：(1)需求不确定：本文将需求视为一直概率分布的随机变量；(2)供应不确定：本文对于供应不确定采用情景分析法。建立以整体供应链利润为目标函数的单目标模型。

二、基本问题描述与模型构建

(一)问题描述

本文的供应中断主要指产品在供应链网络中上游，例如供应商设备损坏或中间环节发生断裂等导致的不能满足市场需求的情况，建立当需求和供应不确定时基于路径的供应链网络设计的非线性规划模型。为解决模型的非线性问题并取得全局最优，本文采用基于黄金分割点的分段线性的方法将其转化为线性规划模型。 本文考虑由I个供应商、J个配送中心和M个零售商组成的三级供应链网络。以3-3-4的三级结构为例，本文主要考虑需求和供应均不确定的情况，认为市场需求是已知分布函数的随机变量。

(二)变量符号说明

为了便于描述，模型中所用到的集合、变量、符号等，如下所示。

(1)I：供应链所有可用供应商的集合；i=1,2，...，I I为正整数；

(2)J：供应链中所偶有候选配送中心的集合；j=1,2，...，J J为正整数；

(3)M：供应链中所有候选零售商的集合；m=1，2，...，M M为正整数；

(4)S：所有可能的中断情景集合 s=1,2，...，S S为正整数；

(5)P：产品集合 p=1,2，...，P P为正整数；

(6)T：供应网络中从供应商出发经过配送中心最后到达零售商的路径集合；

(7)T(i)：从供应商i出发的所有路径集合；

(8)T(j)：经过配送中心j的所有路径集合；

(9)T(m)：到达零售商m的所有路径集合；

(10)Bj：在候选位置启动配送中心j的固定成本；

(11)Cm：在候选位置选择零售商m的固定成本；

(12)Dmp：产品p在市场m的需求量，是已知分布函数的随机变量；

(13)E(Dmp)：产品p在市场m需求量的均值；

(14)F(Dmp)：产品p在市场m需求量的累积分布函数；

(15)capip：供应商i对产品p的生产能力限制；

(16)budg：供应链上的建设预算；

(17)Pmp：产品p在市场m上的单价；

(18)SVmp：产品p在市场m上剩余产品的残值；

(19)LSmp：产品p在市场m的未满足市场需求的单位短缺成本；

(20)Mpt：生产单位成本、产品在路径上的运输单位成本、配送中心的单位存储成本、零售商对产品的单位处理成本之和；

(21)Prs：情景s发生的概率；

(22)Bst：若情景s发生时路径t可用为1，否则为0，是个0-1参数。

(23)另外，a+=max{a,0} ,a∧b=min{a,b} 。

(24)xpst：情景s下产品p经过路径t上的数量；

(25)wj：是0-1变量，若在候选位置启动配送中心j为1，否则为0；

(26)vm：是0-1变量，若在候选位置选择零售商m为0，否则为0。

(三)模型的构建

当供应中断发生时，在不同情境s中市场m的利润为Πms

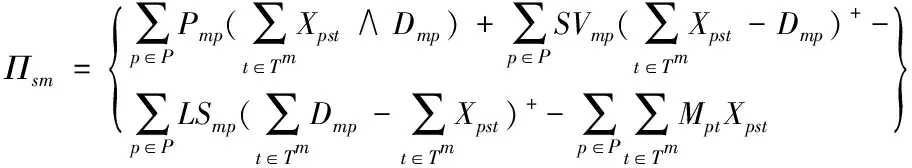
(2.1)

在式(2.1)中，第一项代表供应链在市场m中的收入=单价×销售产品的数量，销售产品的数量=路径中的产品与市场需求的最小值；第二项代表产品销售期末的残值=剩余产品的单位残值×销售期末的剩余产品数量；第三项代表未满足需求的短缺成本=销售期末的单位短缺成本×销售期末的短缺数量；第四项代表沿着路径，产品的处理成本=单位处理成本×路径中的产品数量。式(2.1)表示市场m在情景s下，整个供应链的利润为整个销售期的销售收入，加上销售期末产品的剩余残值，减去未满足市场需求的短缺成本，减去为到达市场m整个路径的处理成本。不同情境s下市场m的利润为

(2.2)

本文计算供应链网络设计中的整个链的预期利润。 现在，解决问题的数学模型可以表示如下：

(2.2)

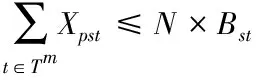
(2.3)

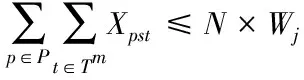
(2.4)

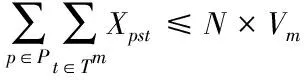
(2.5)

(2.6)

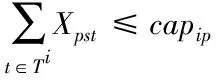
(2.7)

Xpst≥0 ∀p∈P∀s∈S∀t∈T

(2.8)

Wj,Vm∈{0，1}∀j∈J∀m∈M

(2.9)

其中，式(2.2)表示目标函数，整个供应链的预期利润；在约束条件中，式(2.3)解释了在每种情况下，只有在该场景中可用的路线才可能出货(N是一个大常量)；式(2.3)和(2.5)表示配送中心、零售商应建设在产品运送的路径上；式(2.6)表示链的投资成本小于预定预算限制；式(2.7)表示供应商的容量限制；式(2.8)表示路径上的产品是非负变量；式(2.9)表示二进制变量，即是否在配送中心j和零售商m处建立设施。

基于黄金分割的分段线性步骤如下：

步骤1：以连续非线性函数f(x)为例，在区间[Xl,Xu] 内，以X1为起点，有Xl=x1，对应的函数值为y1，以x1为起点的第i个黄金分割点x2=x1+0.618iL(L为整个区间的长度)，对应的函数值为y2。

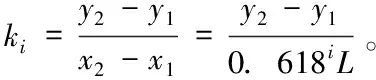
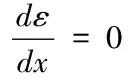
步骤4：同样的方法，以x2为起点，重复步骤1-3，进行下一段的线性处理，知道找出区间[Xl,Xu] 的线性分段函数。

此时会会产生新的参数和变量，如下：

(1)Nm：表示对市场m划分的区间集合；

(2)unm：是第nm段区间的上界；

(3)dnm：是第nm段区间的下界；

(4)anm：是第nm段区间上进行线性替代得到的斜率；

(5)bnm：是第nm段区间上进行线性替代得到的截距；

(6)Xnmpst：情景s下产品p经过路径t在每一段nm上的数量；

(7)θnmps：是0-1变量，表示若最优决策变量落在第nm段区间上则为1，否则为0；

三、结束语

本文首先建立当需求和供应不确定时基于路径的供应链网络设计的非线性规划模型。为解决模型的非线性问题并取得全局最优，本文采用基于黄金分割点的分段线性的方法将其转化为线性规划模型。结果得出，随着时间的变化，供应商的磨损不断增大，中断的概率不断增加，模型会选择剔除较为昂贵和需求相对较少的路径，整个供应链的预期利润也在不断减少。