刺绣机针杆机构运动精度的灵敏度分析

郭惠昕， 张干清

(长沙学院 机电工程学院， 湖南 长沙 410003)

电脑自动刺绣机的刺布机构(即针杆机构)是一个较为复杂的平面连杆机构。文献[1]介绍了GY4-1型绣花机的传动系统及针杆机构的组成和工作原理，并对针杆的运动规律进行了分析，其中特别指出：由于该机构运动环节多、累计误差上升，导致装配调试中出现针杆轴向窜动量偏大的问题(实质上就是针杆运动误差偏大的问题)。针杆机构是形成刺绣线迹的重要机构之一，直接影响绣品的刺绣质量，因此，针杆的运动精度分析是刺绣精度分析研究的重要基础内容[2]。目前，相关研究思路主要体现在以下几个方面：1)在不考虑机构制造误差的情况下，对针杆机构的运动规律进行分析与计算[3-4]；2)计入机构各杆长的制造误差，对刺绣机的针杆运动精度进行分析和对比[5]；3)在计入机构的各杆长制造误差及运动副间隙影响的前提下，探讨机构各杆长基本尺寸及其制造公差的优化设计问题[6]。综合现有文献来看，现有的研究成果基本聚焦在针杆运动误差的分析与设计计算上，尚未能很好地解决文献[1]中指出的针杆运动误差偏大的问题。

要提高针杆机构的刺绣精度，必须提高针杆机构各构件的加工制造精度等级，同时要提高针杆机构的组装质量[2]。虽然，普遍提高各构件的制造精度肯定能提高针杆的刺绣精度，但是这种方法无疑也会导致机器制造成本的大幅增加。实际上，针杆的运动误差是机构各杆长的基本尺寸及其制造误差、各运动副的制造误差(即运动副的间隙)等众多影响因素的非线性函数，且各个因素影响针杆运动精度的重要度并不相同。若能找到影响针杆运动精度的重要因素或关键因素，就可以在维持非重要因素的制造精度不变的情况下，仅仅针对性地提高这些重要因素的制造精度，从而达到既可有效提高针杆运动精度，有效控制制造成本的目的。

基于上述分析，本文考虑针杆机构各构件的杆长制造误差以及运动副间隙等因素的影响，运用Sobol′全局灵敏度分析方法[7]对针杆运动精度进行灵敏度分析；根据灵敏度分析结果，对各影响因素的重要度进行排序，找到导致针杆实际运动出现较大误差的关键因素；然后，针对关键因素采取针对性的有效措施进行机构设计的优化。本文方法可有效地提高针杆的刺绣精度，对提高刺绣机的设计质量具有实际意义。

1 Sobol′全局灵敏度分析方法简介

Sobol′方法[7-8]是一种基于模型分解和方差分析的全局灵敏度分析方法，可解决具有随机变量的系统灵敏度分析问题。设所研究的系统模型为

f=f(x)，x=(x1,x2,…,xn)

(1)

式中：x∈In，I为单位区间[0,1]，In为n维单位超立方体。Sobol′方法的基本思想是把f(x)分解为2n项之和[7]，即：

(2)

式中：1≤i1≤…≤is≤n。则，f(x)的总方差为

(3)

式中：所有积分的积分域均为In。f(x)的偏方差为

(4)

Si=Di/D

(5)

(6)

式(3)～(6)中的f0及Di等统计量可采用蒙特卡洛方法进行随机模拟计算[8-9]。

2 针杆机构运动精度的数学模型

自动刺绣机的针杆机构[1-2]如图1所示。曲柄①为主动件，由调速电动机驱动绕A点作逆时针转动；曲柄转角φ=φ1-φ0，φ0为当曲柄①与连杆②共线时曲柄①与铅垂线之间的夹角。

①—曲柄；②—连杆图1 针杆机构示意图Fig.1 Schematic diagram of needle bar mechanism

该机构是一个比较复杂的平面连杆机构，其几何参数有如下几何关系[1-2]：

(7)

式中lAB为曲柄①的杆长，其他构件长度的表示与此类似。

针杆的位移y可由下式计算：

(8)

其中：

(9)

式(8)中没有考虑运动副的间隙。现引入有效杆长的概念，计入回转副间隙的影响，用有效杆长[6,10]替代上述公式中的杆长，则针杆位移可表达为

y=y(φ,x,z)

(10)

式中：x=(x1,x2,…,x14)，z=(z1,z2,…,z6)。随机变量x为考虑各杆长的制造误差以及各回转副间隙引起的偏心距rk后的机构几何尺寸集合，噪声因素z为各回转副偏心距rk的随机分布方位角δk的集合；k=(a,b,…,f)，各k值分别与图1中各回转副的大写字母编号对应。x和z的所有元素均为随机变量。

GY4-1型电脑自动刺绣机的原型机为日本田岛的TMEF912刺绣机，文献[3]给出了该原型机37个特定曲柄转角φi值对应的针杆位移实测值y0i，(i=1,2,…,37)。为了检验GY4-1是否达到原型机的性能，取

(11)

式中：yi为GY4-1型电脑自动刺透机在37个特定曲柄转角φi值对应的针杆位移；yi用式(10)进行计算。

显见，F的值越小，则针杆的运动精度越高，因此，式(11)可作为表征针杆机构运动精度的数学模型。

3 针杆机构运动精度的灵敏度分析

3.1 针杆机构运动精度的影响因素

针杆运动精度的灵敏度分析需要找到导致针杆实际运动出现较大误差的关键因素。现以针杆机构的一种已知设计方案[6]为例进行灵敏度分析探讨。

以式(11)作为灵敏度分析数学模型，其中，运动精度影响因素x和z的各元素及其分布规律列于表1。表中有关变量的均值[6]分别为：μ1=47.5，μ2=15.3，μ3=54.0，μ4=10.1，μ5=52.5，μ6=27.6，μ7=55.3，μ8=18.4。

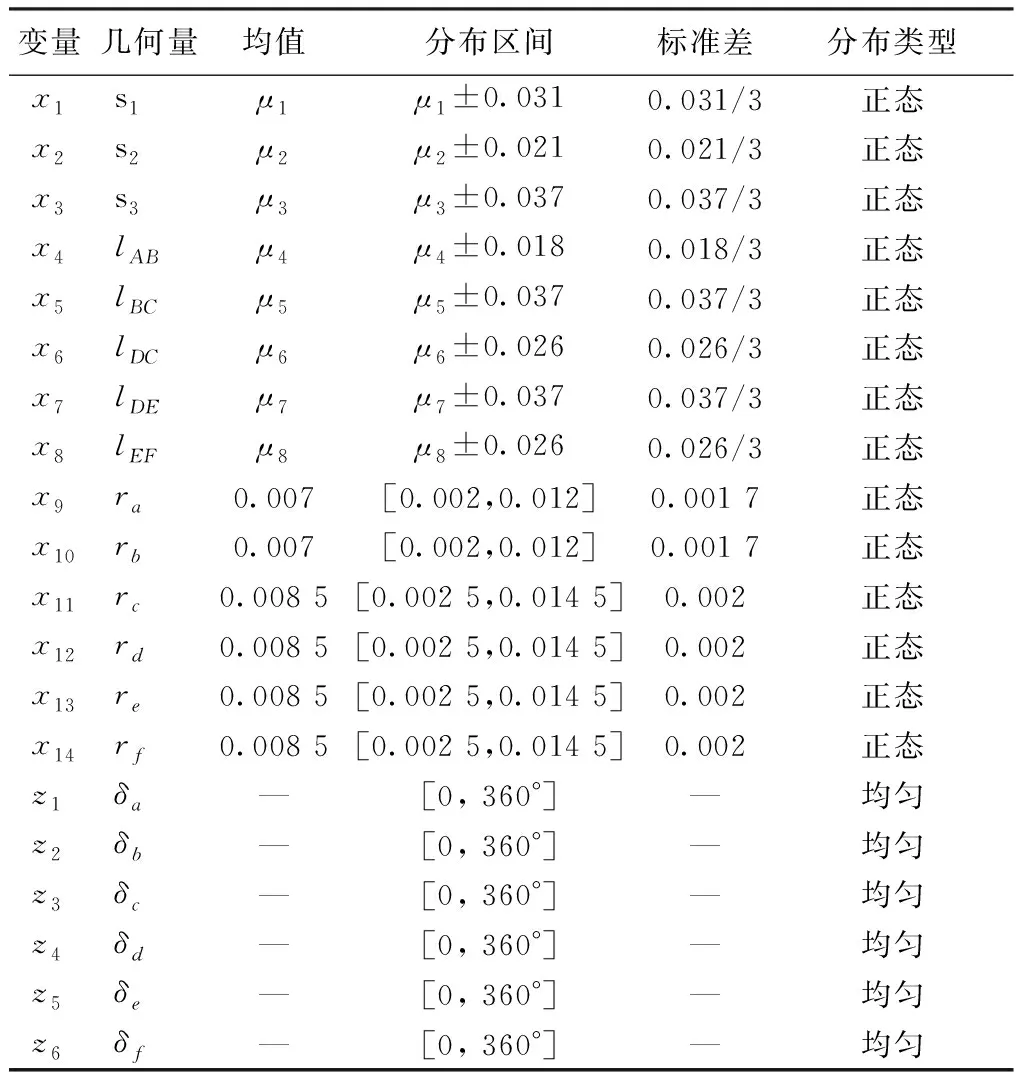
表1 针杆运动精度的影响因素及其分布规律Tab.1 Influence factors and distribution rules of needle bar motion precision

值得说明的是，z对针杆位移的精度有影响，但z为设计制造过程中的不可控因素，因此，仅需分析x的14个元素对针杆位移精度的灵敏度。

3.2 灵敏度分析及结论

在MatLab平台上编写基于Sobol′方法的灵敏度分析蒙特卡洛模拟程序。为保证随机模拟过程中的抽样均匀，抽样方法可采用抽样均匀性较好的拉丁超立方抽样方法[11]或Sobol′随机序列法[12]，本文编程采用后者。

根据灵敏度分析结果，按x各元素的总灵敏度指标值大小进行排序，结果如图2所示。

图2 优化前总灵敏度的条形图Fig.2 Bar chart of total sensitivities before optimization

由图2可得如下结论：总灵敏度指标值较大的有4个因素，其总灵敏度值Stot依次是Stot(x5)=0.713 915，Stot(x1)=0.201 118，Stot(x8)=0.101 174，Stot(x6)=0.077 467。灵敏度值越大，说明该影响因素对针杆运动精度的影响越明显，因此，这4个因素就是影响针杆机构刺绣精度的重要因素。其中，总灵敏度值最大的x5是关键因素。总灵敏度值很小甚至接近于零的那些因素，属于非重要因素，它们对针杆机构运动精度的影响也就很小。

4 基于灵敏度分析的针杆机构优化

灵敏度分析的目的是要找到影响针杆机构运动精度的重要因素，并指导设计者针对性地采取措施，以便进一步优化机构的设计质量。为此，在上节所述针杆机构的设计方案[6](称为优化前方案)基础上，进行机构的进一步优化设计。

4.1 优化思路与优化方案

由图2可知，x5为影响针杆运动精度的关键因素，代表图1中的连杆②的长度及其制造误差。表1中所示lBC的偏差是±0.037，精度等级是IT9。现维持x5的均值不变，即仍取μ5=52.5，但将其制造精度等级提高1级，其尺寸偏差变为±0.023。其他所有尺寸及其精度等级仍保持表1中的参数不变，即和优化前方案一样。

4.2 优化效果分析对比

对上述优化方案再进行一次灵敏度分析，分析结果及其灵敏度排序见图3。

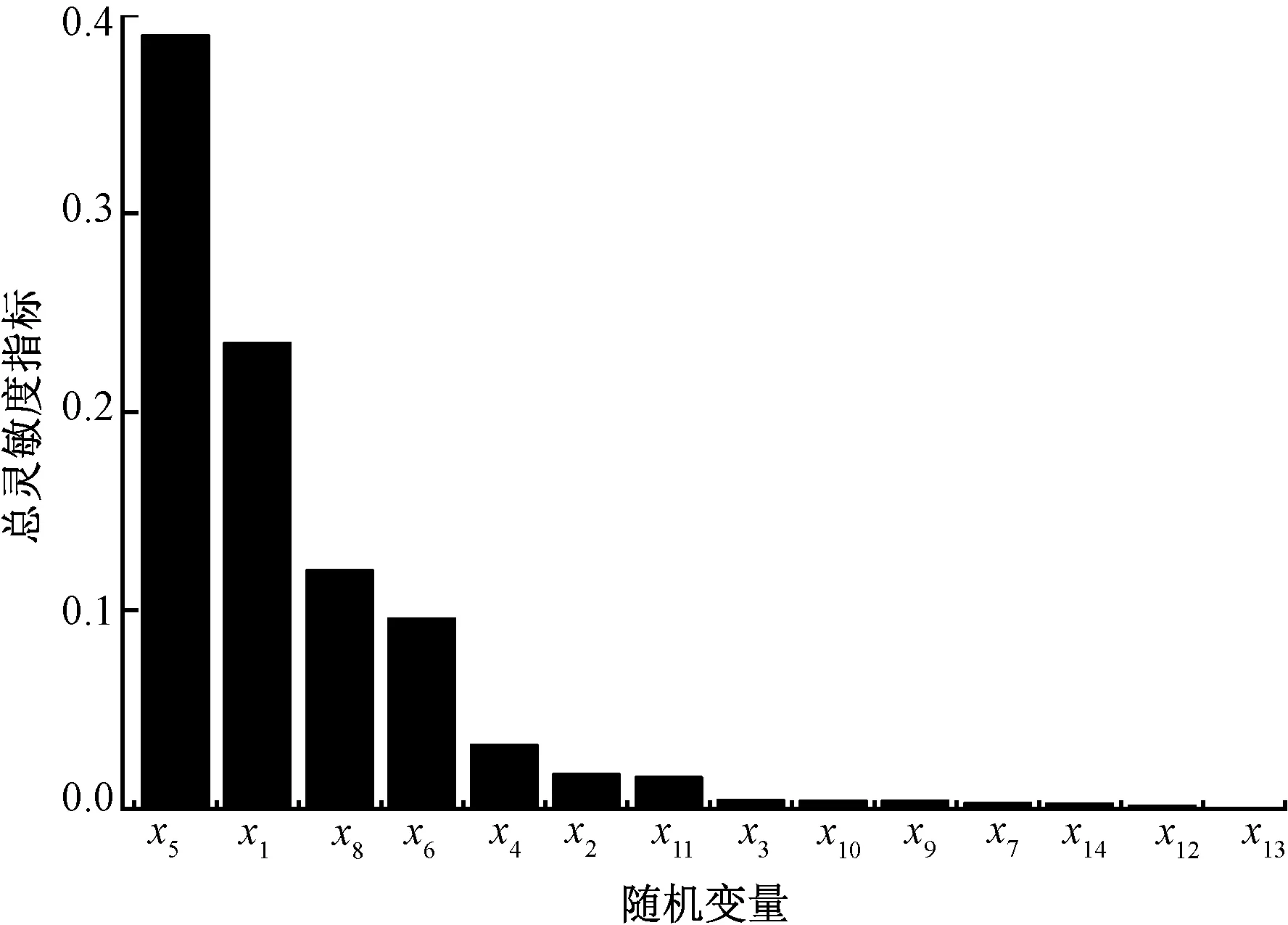
图3 优化后总灵敏度的条形图Fig.3 Bar chart of total sensitivities after optimization

此时，4个重要因素的总灵敏度值发生了变化，它们依次是：Stot(x5)=0.389 891，Stot(x1)=0.234 580，Stot(x8)=0.120 147，Stot(x6)=0.095 805。x5仍为影响针杆运动精度的关键因素，但其总灵敏度值已经大幅减小。

经过上述的进一步优化后，针杆机构的运动精度应该有所提高。为检验优化效果，针对第2节中提到的37个特定曲柄转角φi值，对针杆位移精度进行随机模拟计算，优化前后2种方案的模拟结果如图4、5所示。

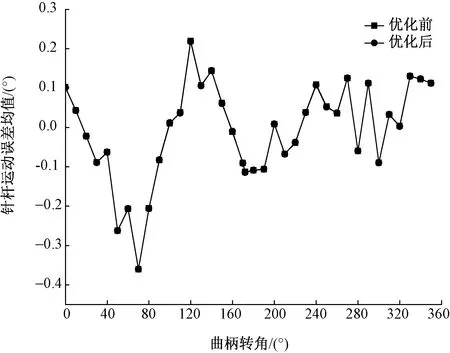
图4 优化前后针杆运动误差的均值Fig.4 Mean values of needle bar motion error before and after optimization

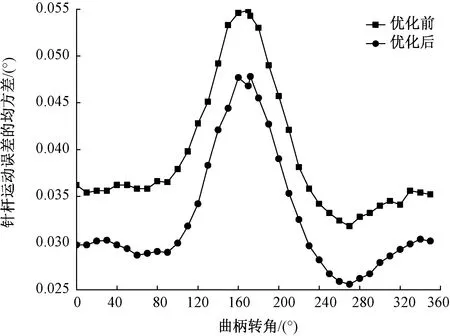
图5 优化前后针杆运动误差的均方差Fig.5 Mean square deviation of needle bar motion error before and after optimization

由于没有改变x(5)(即lBC)的均值，故进一步优化后针杆位移误差的均值和优化前基本相同，图4中2条曲线基本重合，但是，优化后针杆位移误差的均方差明显减小(见图5)。文献[1]指出了GY4-1型绣花机在装配调试中出现的针杆轴向窜动量偏大的问题，而影响窜动量大小的主要因素是针杆位移误差的离散性。针杆运动误差的均方差越小，其位移误差的离散性越小，因此，经过进一步优化后，针杆轴向窜动量将减小，针杆位移精度的稳健性得到进一步提高。

5 结 论

1) 灵敏度分析是研究与分析一个模型 (或系统)的输出(或响应)的变化对系统参数的敏感程度的方法。通过灵敏度分析可以确定出哪些参数对模型输出有较大的影响，并可确定出影响模型输出变异的重要因素。研究针杆机构运动精度的灵敏度问题，可找到影响其运动精度的关键因素，以便对现有设计方案进行评价，并为进一步优化提供依据，具有重要的工程意义。

2) 采用Sobol′方法对文献[6]中针杆机构优化设计方案进行了全局灵敏度分析，求解出影响针杆运动精度的所有14个变量的总灵敏度，找出14个变量中的4个重要因素及1个关键因素。其中，连杆长度是关键因素。

3) 在灵敏度分析的基础上，采取针对性的有效措施，通过减少关键因素连杆长度的制造误差，对原设计方案进行了进一步优化。通过随机模拟得到了37个特定曲柄转角处的针杆位移误差的均值和均方差。对比可见，进一步优化后，针杆位移误差的均方差明显减小，有效地提高了机构运动精度及其稳健性，优化了针杆机构的设计质量。

FZXB