毛织物孔隙特征与透湿性关系

张文娟， 纪 峰， 张瑞云， 赵晓杰,， 王 妮， 王俊丽， 张建祥

(1. 东华大学 纺织面料技术教育部重点实验室， 上海 201620； 2. 鲁泰纺织股份有限公司， 山东 淄博 255100；3. 上海嘉麟杰纺织品股份有限公司， 上海 201504)

羊毛是一种天然的纺织纤维，具有许多优良特性，随着人们生活水平提高，对毛织物的湿舒适性需求也在提高。织物对隐式汗的通透能力影响其着装舒适性，而织物对隐式汗的传输取决于其孔隙结构[1]。

透气性、透湿性、导液性分别用于表示织物对空气、水蒸气和液态水的通过能力，其作用机制、表征指标和测试方法各不相同。对于透气性能：徐广标等[2]在23种精纺毛型织物实验数据基础上，探讨了织物孔隙分布的特征及孔隙与织物结构和透气性能的关系；吴海军等[3]探讨了毛织物孔隙分布的特征，测试并定量分析了毛织物的孔隙与织物结构对透气性的影响。织物孔隙结构的差动效应往往用于分析其导液现象。范菲等[4-5]认为孔径尺寸和孔径分布都对织物的芯吸速率起决定性作用，并根据毛细差动原理分析了毛细孔分布与双层组合织物的芯吸性能的关系；姚穆等[6]提出了织物湿传导通道的3种形式，指出了织物中透湿孔洞有多种多层次结构，在湿传导过程中的表现和作用各不相同。YANILMAZ M等[7-8]研究了孔隙率、孔径分布和孔径大小对其芯吸性能的影响。对透气性和导液性的研究都涉及织物内部孔隙结构对气、液态流体的作用机制，这对研究孔隙结构对织物透湿性的作用机制有参考作用。

早在1985年李毅等[9]探讨了5种毛呢织物的厚度、填充率与其热湿舒适性表征指标的关系；姚穆等[10]研究了织物的透湿过程，涉及了水蒸气在湿空气中的扩散及毛细管中水蒸气的蒸发的过程及理论方程；FANGUEIRO R等[11]研究了羊毛与聚酯型纤维混合纱线的导液性与干燥蒸发性能。LI Yi等[12-13]建立了关于羊毛织物热湿扩散的数学模型，用于预测羊毛织物热、湿扩散性能。可以看到，用于分析和预测透湿性的2类模型，纯理论模型因做了较多理想化假设其分析结果往往与实际情形有差距，而经验模型只能在有限范围内根据经验数据做出相对准确的预测。

织物内部孔隙情况(尺寸、分布等)，对湿汽传输有相当的决定作用，直接影响了湿舒适性。本文拟建立孔隙结构参数与湿阻的关系模型。采用体积孔隙率、表面孔隙率和平均孔径3个指标各从不同角度描述织物中孔隙情况，使用回归分析方法分别建立了3个孔隙指标与湿阻的多项式回归关系经验模型。

1 实验部分

1.1 试样选择

本文选用由嘉麟杰纺织品股份有限公司、江苏阳光集团提供的24块羊毛织物试样，包括14块机织面料，10块针织面料。织物基本结构参数如表1所示。

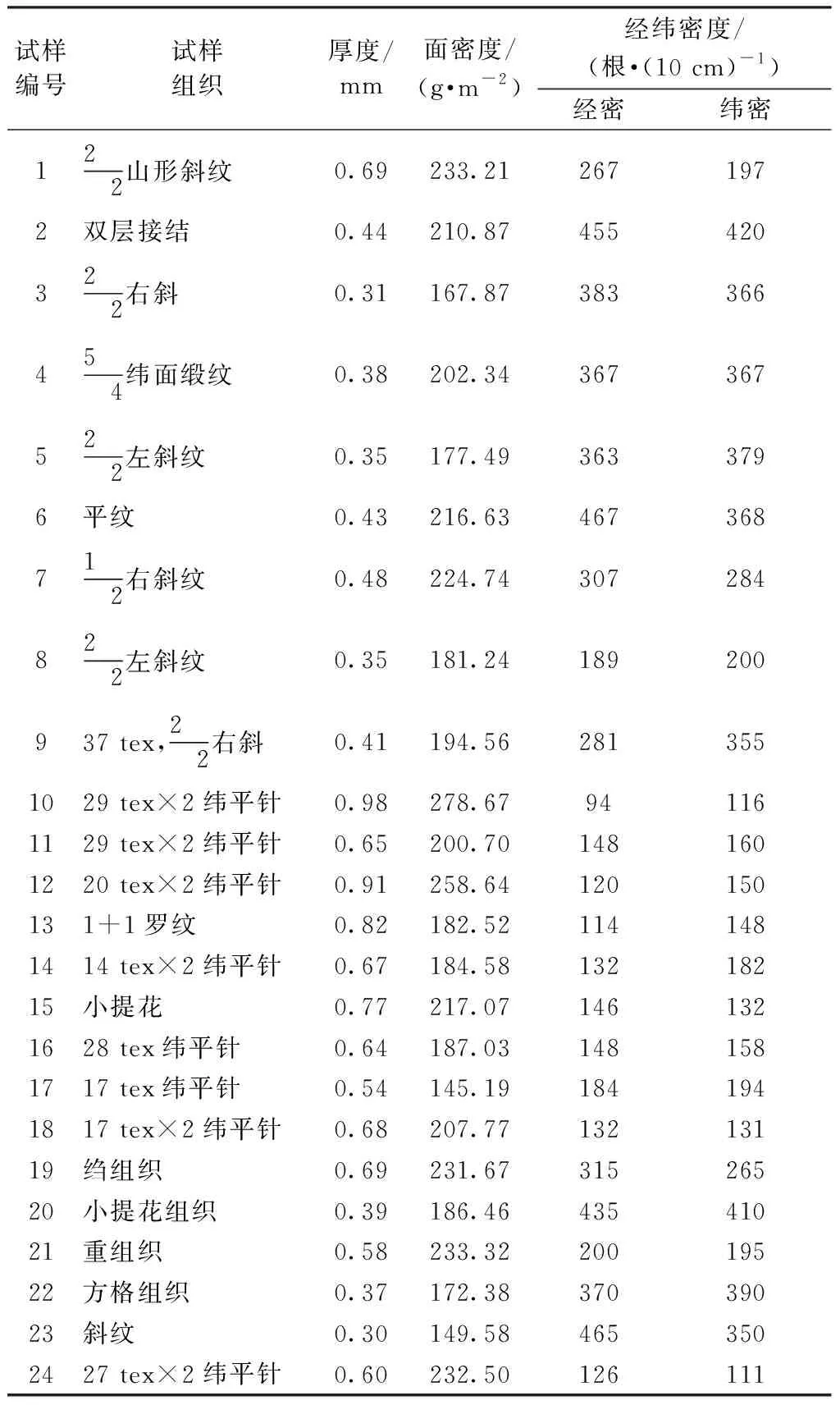
表1 织物结构参数Tab.1 Structural parameters of fabric samples

1.2 实验设计

1.2.1孔隙率及平均孔径测试

本文采用体积孔隙率[14-15]、表面孔隙率和平均孔径3个指标表征织物内部孔隙特征。

体积孔隙率是指织物中的孔隙体积对其总体积的比值，是衡量织物内部孔隙量的指标。体积孔隙率计算公式如式(1)～(3)所示。

(1)

(2)

(3)

式中：εv为织物的体积孔隙率，%；Vf为织物的外观体积，包括织物外轮廓全部体积，cm3；Vy为纱线体积，cm3；δy为纱线的体积密度，g/cm3；Kd为毛纱线直径系数，这里取1.13；Tt为纱线的线密度，tex；d为纱线的直径，mm；G为调湿后的质量，一般指公定回潮条件下的数值，g。

表面孔隙率是指织物朝大气一侧孔隙的面积占总面积的百分比，采用计算机图形处理法计算得到表面孔隙率。本文用MatLab软件对织物表面图像进行二值化处理，如图1所示。在二值化图像中白色像素区表示织物中被纱线占据的区域，黑色像素区则表示孔隙区域。表面孔隙率计算公式见式(4),表面孔隙率值越大，表示织物大气一侧孔面积所占比值越大。

(4)

式中：εs为织物的表面积孔隙率，%；Φu为织物表面黑色像素点个数；Φa为织物表面像素点个数。

图1 Matlab图像处理Fig.1 MatLab image processing. (a) Original image; (b) Grayscale image; (c) Enhanced image; (d) Binarized image

织物表面孔隙率侧重反映织物外表面的孔隙量。体积孔隙率则表征了织物结构体内部的孔隙体积百分含量。表面孔隙率提取时剔除了表面封闭假孔隙区域，而体积孔隙率计算中包含了由于纱线滑移等原因造成的封闭孔隙，因此采用的2种孔隙率分别反映了织物外侧和内部孔隙的含量。

平均孔径指织物内部所有孔隙当量直径的平均值，表示孔径的平均尺寸。采用CFP-1100AI型多功能孔径仪测量织物孔径。通过测量样品受到的瞬时压力和流经样品孔隙的气体或液体流量，可获得压力—流量的变化曲线。根据ASTM标准计算出平均孔径指标，主要依据公式见式(5)[3]。

D=4γcosθ/P

(5)

式中：D为孔隙的当量直径，μm；γ为液体的表面张力，mN/m；θ为接触角，(°)；P为压差，Pa。

1.2.2透湿性测试

湿阻是纺织品处于稳定的水蒸气压力梯度的条件下通过一定面积的蒸发热流量，反映隐式汗透过织物的能力。湿阻值越小，表示湿汽透过能力越强，合适的湿阻值使人体感觉舒适。

实验选用YG606型热阻湿阻测试仪模拟人体皮肤散发出隐式汗从而测试服装面料对汽态(隐式汗)通过的阻力(湿阻)。实验按照GB/T 11048—2008《纺织品 生理舒适性 稳态条件下热阻和湿阻的测定 (蒸发热板法)》进行。采用式(6)计算湿阻。

(6)

式中：Ret为织物的湿阻，m2·Pa/W；Pm为饱和水蒸气压力，Pa；Pa为指水蒸汽压力，Pa；A为试验板的面积，m2；H为提供给测试面板的加热功率，W；ΔHe为湿阻Ret测定中加热功率的修正量；Reto为测定湿阻而确定的仪器常数，m2·Pa/W。

2 实验结果

24份纯毛织物试样的孔隙率、平均孔径及湿阻结果见表2。

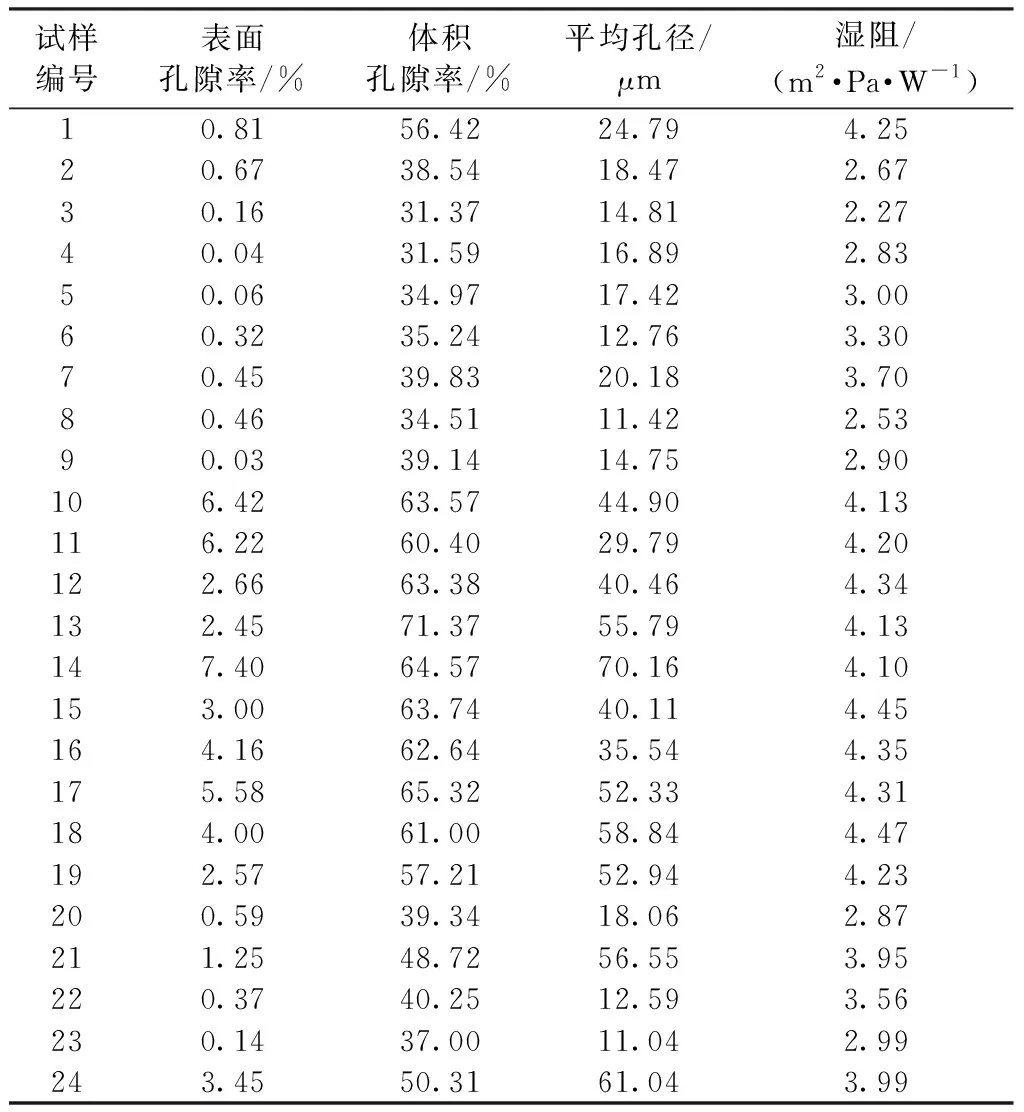
表2 织物试样测试数据Tab.2 Test data of fabric samples

通过实验数据观察到，机织物的表面孔隙率一般低于针织物。在机织物中，以试样9、23为代表的斜纹组织，其经纬组织密度较高，即使在纱线线密度较小的情况下，其外表面组织结构相对致密，使表面孔隙率显著较小。在针织物中，以试样14为代表的纬平针组织，因纵、横向组织结构疏松，使其表面孔隙率、体积孔隙率和平均孔径都显著较大。

表2中数据同时表明，表面孔隙率、体积孔隙率和平均孔径之间的相关性不明显，在上述试样中，表面孔隙率相对最小的试样，如试样4、5、9，其体积孔隙率和平均孔径并不是显著小的。

3 织物孔隙透湿性回归模型的建立

本文采用一元多项式回归分析建立织物孔隙特征与其透湿性的经验相关模型，该方法是研究1个因变量与1个或多个自变量间多项式的回归分析方法，其显著特点是可通过增加自变量的高次项对实测点进行尽可能地逼近。

3.1 体积孔隙率与湿阻的回归模型

具体地，首先采用表2中的体积孔隙率与湿阻的实验数据，通过SPSS软件进行毛织物体积孔隙率与湿阻的一元高次函数的回归分析见式(7)，并拟合出二者的关系曲线图，如图2所示。

(7)

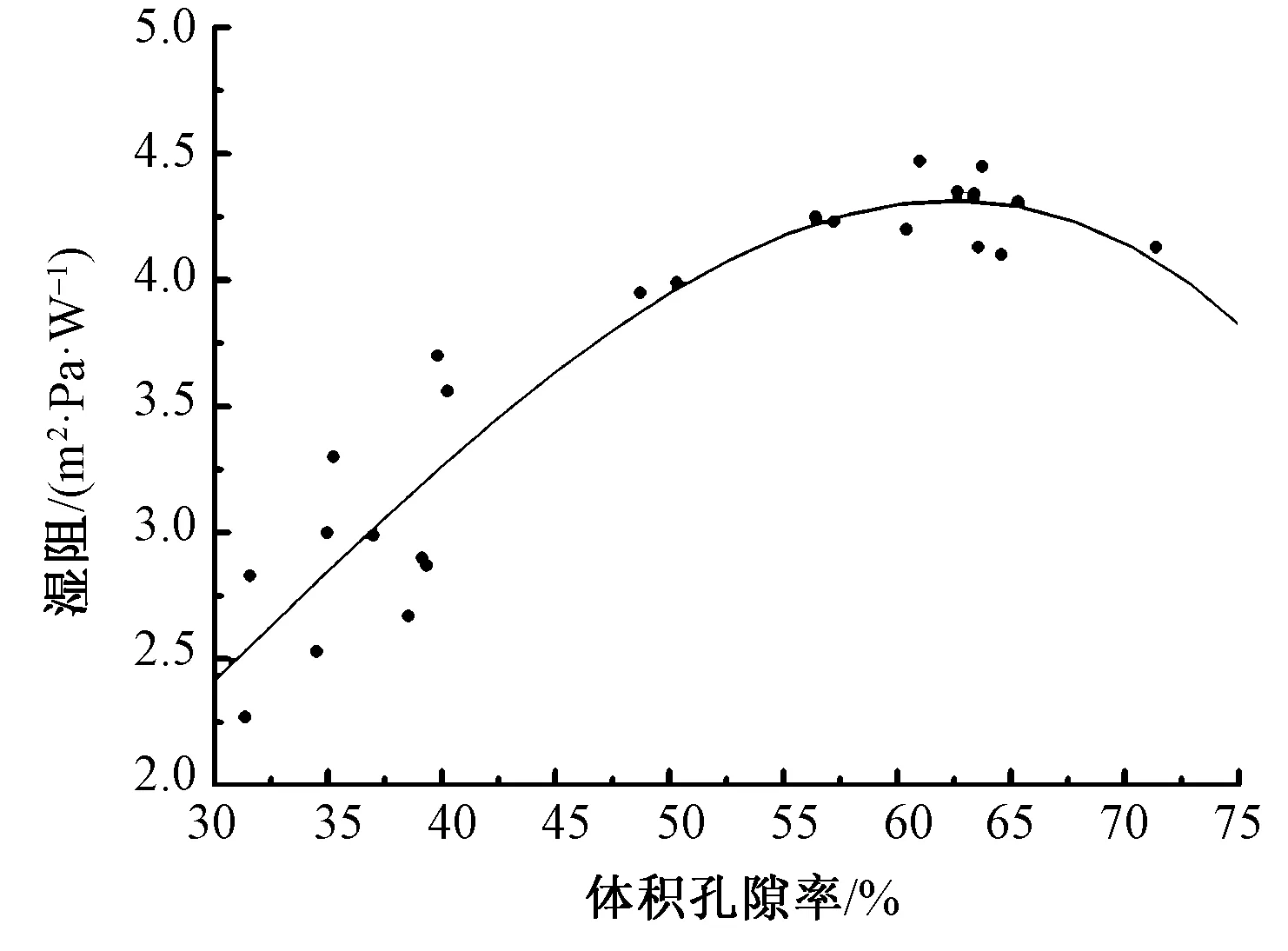
图2 织物体积孔隙率与湿阻的关系曲线Fig.2 Relationship between fabric volume porosity and wet resistance

该方程的判定系数R2=0.87，R2越接近1表示模型的拟合效果越好。

表3示出方差分析，对回归关系进行F检验。

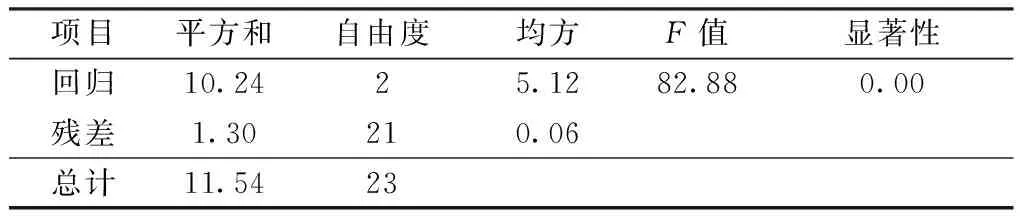
表3 方差分析表Tab.3 Variance analysis

由自由度为2和21，查F值表得F=82.88>F0.05(2,21)=3.47，表明该回归关系显著。

根据图2所示数据变化趋势大致划分2个阶段：第1阶段，体积孔隙率增大湿阻随之明显增大；第2阶段，湿阻达到一定峰值区域，此后体积孔隙率增大湿阻不再随之明显增加。

第1阶段：体积孔隙率范围在30%～60%之间时，随着体积孔隙率上升，湿阻呈现上升趋势。说明此范围织物内部的孔隙含量对湿气传输的影响作用不占主导，织物两侧湿气的传导在更高程度上受孔隙的形状和分布状态的影响。

第2阶段：当体积孔隙率超过60%左右时，织物两侧的空气更容易通过显著增大的孔隙进出孔隙，两侧湿气能够在微孔区域内以对流的形式参与交换，令湿阻不再继续增大。

从体积孔隙率与湿阻的关系曲线中可以看出，在符合其他服用条件的情况下，可根据服用舒适性需求设计合适的体积孔隙率。若用于户外的运动服装则选择体积孔隙率为(40±10)%且厚度值在0.30～0.48 mm范围，此范围内湿阻在4.0以下且体积孔隙率对湿阻的影响较显著，在可设计的范围。

3.2 表面孔隙率与湿阻的回归模型

由MatLab图像处理测得的表面孔隙率为自变量，湿阻为因变量，采用SPSS软件分析得到图3所示的关系曲线。织物表面孔隙率与湿阻之间的回归方程为式(8)，方程拟合度判定系数R2=0.75，模型拟合效果较好。

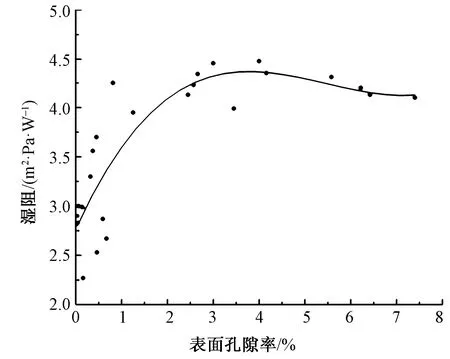
图3 织物表面孔隙率与湿阻的关系曲线Fig.3 Relation between fabric surface porosity and wet resistance

y=1.3×10-2x3-0.21x2+1.03x+2.77

(8)

由自由度为3和20，查F值表得F=19.52>F0.05(3,20)=3.10，表明该回归关系显著。

从图3可知，当表面孔隙率在0%～3%范围内时，8块机织物和3块针织物的湿阻随着表面孔隙率增加而增大。表面孔隙率在0%～1.5%范围内时，湿阻值比较离散，一定程度上表明在这个范围内表面孔隙率对湿阻的预测失效，说明应是其他因素起主要作用，如毛织物紧密程度、织物表面或内部毛羽；而当表面孔隙率大于1.5%时，表面孔隙率对湿阻的预测能力显现，当同样浓度的隐式汗接触织物表面时，孔隙率相对小的织物在其表面液化会相对多一些，传输到织物另一面的较少。

当表面孔隙率大于3%时，随着表面孔隙率增加，气体对流效应起主导作用，湿气流通能力增大，湿阻随表面孔隙率的增大呈缓慢下降趋势。

3.3 平均孔径与湿阻的回归模型

以CFP-1100AI 型多功能孔径仪测量织物平均孔径值为自变量，湿阻值为因变量建立的关系曲线如图4所示。织物平均孔径与湿阻的回归方程见式(9)，方程的判定系数R2=0.74，模型的拟合效果较好。

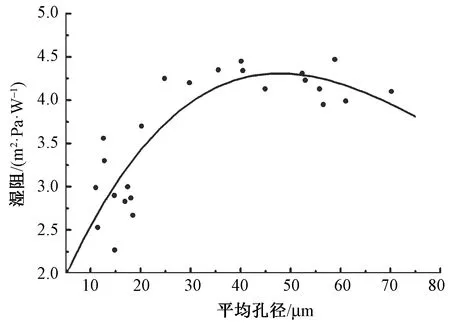
图4 平均孔径与湿阻的关系曲线Fig.4 Relation between average pore size and wet resistance

(9)

由自由度为3和20，查F值表得F=18.99>F0.05(3,20)=3.10，表明该回归关系显著。

从图4可知，当平均孔径在10～45 μm之间时，随着平均孔径增大，湿阻呈现上升趋势，这与隐式汗在织物内部可能发生液化有关，液体传导依靠毛细孔径，而织物孔径增大会导致毛细管减小。除此之外，孔径较大的织物其内部发生液化的程度也大，透过织物的湿气量减少。当平均孔径大于45 μm时，这时对流现象开始变得明显，接触阻碍等相对变弱，表现为随着平均孔径增大，湿阻降低。

4 结 论

1)分别对体积孔隙率、表面孔隙率、平均孔径与湿阻的关系进行统计分析建立经验回归模型，3个多项式模型总体呈现先上升后下降的趋势。

2)对于本文选用的试样，在体积孔隙率与湿阻的回归模型中，体积孔隙率在达到60%时出现拐点；表面孔隙率与湿阻的回归模型中，表面孔隙率在3%左右时出现拐点；平均孔径与湿阻的回归模型中，平均孔径在45 μm左右时出现拐点。

3)当表面孔隙率在0%～1.5%范围内时，湿阻值比较离散，一定程度上表明在这个范围内表面孔隙率对湿阻的预测失效，说明在该范围内表面孔隙状态对湿阻的影响不是主导因素；当表面孔隙率大于1.5%时，通过表面孔隙率对湿阻的预测效果开始显现。

FZXB