基于线性LTSA算法维数约减的软件缺陷预测研究
王玉红,范 菁,曲金帅,冯景义
(云南民族大学 云南省高校信息与通信安全灾备重点实验室,云南 昆明650500)
软件缺陷预测技术旨在利用已知的度量元和标签训练样本,获取软件缺陷分布预测模型,对未知的软件模块进行二值分类(即有缺陷和无缺陷)[1],预测出软件系统中高风险模块,合理分配软件测试资源[2].而基于软件相关的度量数据往往为高维且非线性的流行结构,获取真实的低维数据结构信息,约减数据维度已成为软件缺陷预测技术研究的关键.软件缺陷预测中多维度量元带来的“维度灾难”,会导致软件缺陷预测精度降低[4].针对此问题,采用局部切空间排列算法(LTSA,local tangent space alignment)的线性逼近进行数据预处理,除去度量属性过多造成的冗余数据信息,构造软件缺陷分布预测模型[3-4].
1 线性 LTSA算法描述
LTSA算法有较高的鲁棒性,但算法不能得到解析形式的映射函数,对于新加入的样本点,需要重新学习才能映射到低维空间.针对LTSA算法无法直接映射新样本点坐标的问题,提出一种LTSA算法的线性逼近,为线性局部切空间排列算法,能够有效学习出映射空间的基向量,从而将新样本点投影到低维线性空间.采用较为简单的线性投影方法,显著特点是计算复杂度较低,计算速度快.
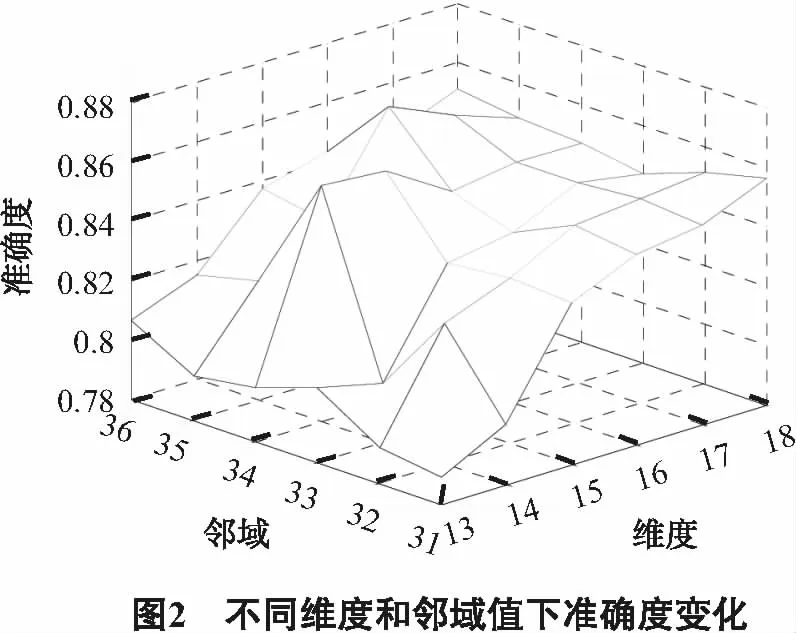
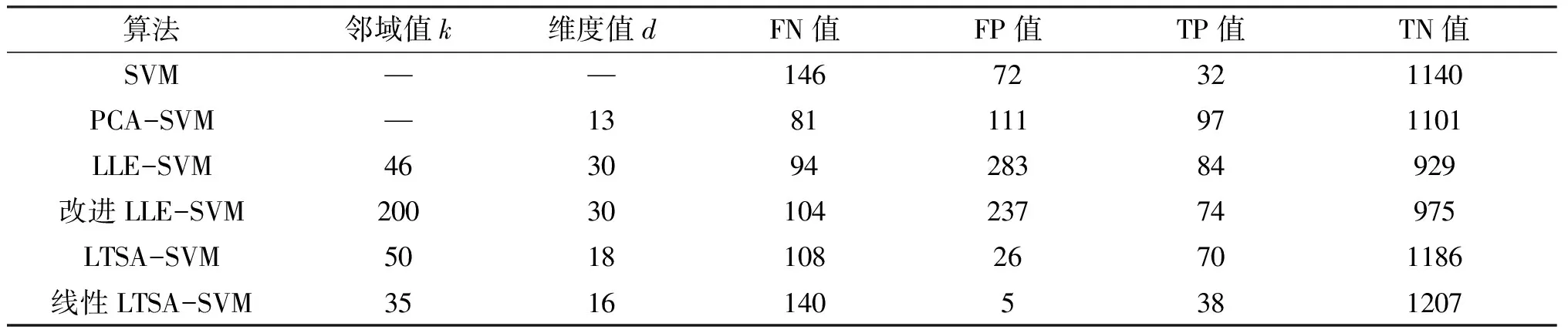
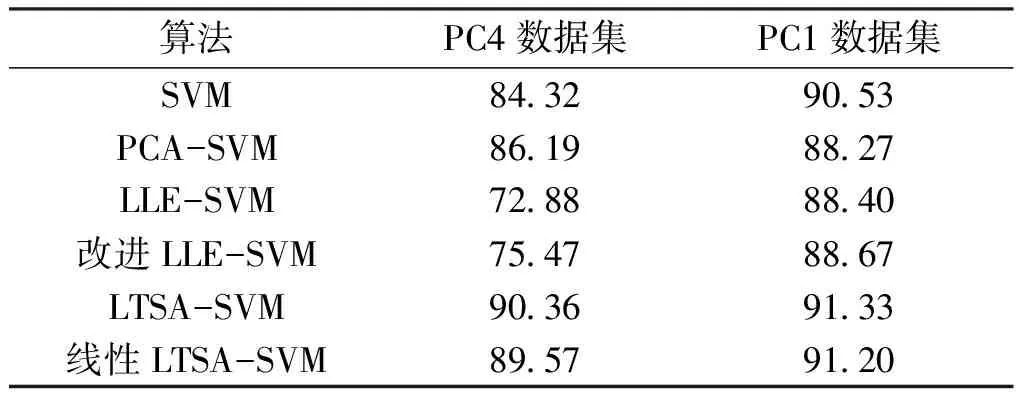
线性LTSA算法的主要思想是寻找一个转换矩阵G,将数据集X∈RD空间通过映射变换矩阵映射到X∈Rd空间,其中,样本点个数为N,且d Y=GTXHN . (1) 其中,HN为中心化矩阵,HN=I-eeT,I为单位矩阵,为元素全1的N维列向量,Y为维数约简后的低维数据集. 第1步,根据KNN准则选取邻域. 选取样本点xi的k近邻xij(邻域包含xi本身)组成邻域矩阵Xi=(xi1,xi2…,xik),i=1,2,…,N,j=1,2,…,k,k为近邻点个数. 第2步,邻域切空间计算. 在邻域矩阵Xi上进行PCA降维,求得邻域内的一组正交基Qi,Qi即为XiHk的前d个最大特征值对应的特征矢量构成的切空间正交基矩阵,将邻域内的样本点投影到Qi上,获取邻域的主要低维流行结构信息. (2) Hk为中心化矩阵,Hk=I-eeT/k,I为单位矩阵,e为元素全1的k维列向量.样本点xi的邻域嵌入坐标如下. (3) 第3步,计算全局坐标排列. 以重构误差最小化为约束条件,保持高维原始样本空间的局部流行结构,重构数据集的本征结构,进行局部切空间的全局坐标排列,目标函数如下. (4) 上述目标函数最小化解的可转化为求解矩阵广义特征值问题. XHNBHNXTα=λXHNXTα . (5) 基于线性LTSA算法软件缺陷预测模型主要流程如图1所示. 首先,选取美国航空航天(NASA)的MDP(metric data program)软件度量项目中的PC4数据集,包含1 399条数据,每条数据由37个属性描述,并在数据末尾处标明了该数据的标签属性,即有无缺陷.实验中将有缺陷模块记为1,无缺陷模块记为-1.其次,降维后的新数据集作为下一步的输入集. 由于支持向量机(support vector machine,SVM)在高维、小采样中表现出优良的特性,且分类结果不受少数离群点决定,所以选用SVM进行二值分类[9,13],核函数选择径向基核函数(radial basis function,RBF),含有的参数为核函数参数δ(g),为评价离群点带来的损失,引入了惩罚因子C. 线性LTSA算法需确定邻域值k和降低维度值d.参考大量文献并多次实验后给定k的取值区间为 [33,38],遵循d 软件缺陷预测技术领域最广泛应用二维混淆矩阵评价模型的预测能力,是国际上公认的、标准化的研究方法,实验中SVM分类可以得到每个样本的标签信息,即有缺陷1或者无缺陷-1,将1预测为-1的数目记为TP,将1预测为-1的数目记为FN,将-1预测为1的数目记为FP,将-1预测为1的数目记为TN,统计得到TP、TN、FP和FN的值.计算得到指标包括准确度、查全率、查准率和F-measure值,本模型主要采用准确度这一评价指标.如表1所示. 表1 混淆矩阵 准确度(Accuracy)表示正确分类的样本总数占测试样本的比例. (6) 查全率(Recall)表示实际和预测值都为有缺陷的样本数目占实际含缺陷的样本总数的比例. (7) 查准率(Precision)表示实际和预测值都为有缺陷的样本数目占预测为含缺陷的样本总数的比例. (8) F-measure值(F值)表示查准率和查全率的调和平均. (9) 选用LTSA算法对PC4数据集降维,采用网格搜索结合10折交叉验证进行实验.得到准确度随维度和邻域的变化,如图2所示. 实验结果证明当k=35,d=16时,评价指标即分类的准确度最高为86.69%,因此模型选取这组参数值进行软件缺陷预测.采用同样的参数选取SVM参数,给定核函数参数的取值区间,步长设置为0.1,惩罚因子C的取值区间,步长设置为0.01.当取34.8,C取0.1时,预测准确度最高为89.57%.统计各模型预测的二维混淆矩阵中数据结果,与传统降维算法模型比较,如表2所示. 表2 不同降维算法的预测值 选用同样的数据集PC4和PC1,与采用流形学习[12]中主要的LLE、LLTSA、NPE算法进行数据降维处理的实验及单一的SVM软件缺陷预测的评价指标比较,如表3所示. 表3 不同数据集预测结果准确度 % 由于不同参考文献中数据集的选取都具有随机性,采用同样的降维算法预测得到的结果会存在一定的差异,所以参考文献[10]中的实验结果有所不同.但该仿真实验是在同一数据集下比较得出的预测准确度,因此,结果对比是有效的. 实验结果表明,采用LLE算法降维处理对邻域点数目的依赖性较大,属性约减的同时,也除去了数据的重要特征.改进LLE算法是在LLE算法的基础上将KNN中根据欧氏距离选取领域点改进为取成对距离(Pairwise距离).以上两种算法预测结果并不理想,针对不同的数据集,改进LLE算法预测效果提高的程度不同,说明LLE算法具有不稳健的解.采用PCA算法在不同数据集上的表现不一致,对于较大的数据集,准确度提高了2%,数据集较小时,评价指标不会提升.LTSA算法能得到更稳定的解,准确度在在两者数据集上分别提高6%和1%左右,线性LTSA算法能在数据集维度和邻域值较小的情况下,达到和LTSA算法近似的结果,并且该算法可直接映射新的样本点,得到显式的映射函数,不需要重新学习高维空间的流行结构.以下表4比较了LTSA和线性LTSA算法的时间成本耗费. 表4 PC4数据集算法的时间成本 s 由此可知,本文算法在软件缺陷预测中表现出极大的优越性,能在邻域点数目较少且维度较低的条件下,直接映射新的样本点,预测精度和LTSA算法结果相近,提高预测准确度,降低了计算的复杂度,预测最优准确度的时间消耗从13.726 9 s降低至6.217 8 s,同样在(k,d)网格参数为6×6的矩阵寻优耗费的时间由267.442 1 s降低至165.98 s,有效提高了软件缺陷预测的效率,减少时间成本. 软件缺陷预测技术能够识别软件系统中的高风险的模块,在软件开发过程中具有重要的指导意义.本文针对软件缺陷预测数据集高维、小采样的特点,采用LTSA算法对数据集的冗余特征进行约减.该模型的主要思想是利用局部特征映射的切空间排列,以重构误差最小为约束,求解全局低维坐标表示.实验结果表明,本文建立的模型可以利用较少的邻域点在更低维度的空间求解得到更加稳健的特征向量,并有效保留了原本样本空间的流行几何结构.但实验各模型并不能有效提高软件缺陷的预测精度,下一步,将结合算法最后线性投影方向,考虑改进线性LTSA算法,提高模型预测的预测精度.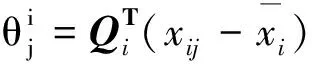
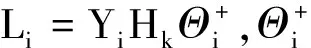
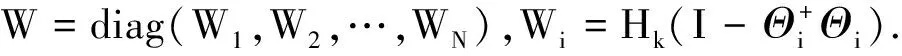
2 软件缺陷预测模型
2.1 模型建立

2.2 模型参数寻优
2.3 模型评价指标

2.4 软件缺陷预测仿真实验

3 结语

