动荷载作用下山区道路边坡耐久性研究
,,, ,
(1.福建农林大学 交通与土木工程学院,福州 350108;2.福州大学 岩土工程与工程地质研究所,福州 350108)
1 研究背景
随着我国经济的快速崛起以及大量基础设施的不断扩建(如高速公路、铁路和水电枢纽等),尤其是在向山区不断延伸,山区边坡工程问题日益突出。在车辆荷载、地震等动荷载的持续作用下,构成基础或边坡的岩土体受环境振动的影响,逐渐产生疲劳损伤、强度劣化,导致其可在较低应力水平下发生显著的变形,最终使“结构体”失效。当前,山区道路建设过程中与边坡工程有关的设计和稳定性评价正逐步考虑动荷载影响,与边坡静力问题相比[1-3],其动力问题更加复杂,而且远未得到应有的研究。
目前,在循环动荷载作用下岩石疲劳损伤过程中的基本变形特性[4-6]、声发射特性[7-8]、CT细观疲劳损伤扩展的初步规律[9]、实时超声波速法的损伤特性[10]和非线性动力损伤力学理论[11-12]等方面已有一些开创性的研究成果。以上研究侧重于室内试验,针对山区道路边坡全生命周期内安全性与耐久性的演变过程以及动荷载作用下山区道路边坡岩体损伤累积至不同阶段时的“存活率”或“破坏概率”的可靠性研究还较少。事实上,动荷载作用下边坡的疲劳稳定性与寿命的变化体现了边坡动力永久变形的累积程度,这种变形的程度反映出边坡发生破坏的概率,即边坡存活率[13]。因此,本文利用威布尔分布的密度函数分析给定条件寿命下的边坡存活情况,建立存活率与累积损伤因子关系;运用有限元强度折减法建立安全系数与疲劳寿命之间的联系,达到以存活率、疲劳寿命和安全系数综合显示实际岩质边坡在其全生命周期内健康情况的目的,并制定山区道路边坡相关预警准则;最后,基于存活率提出耐久性因子,实现从稳定性与疲劳寿命两方面控制边坡工程的安全性与耐久性。
2 威布尔分布模型
威布尔分布的分布函数定义为[14]
(1)
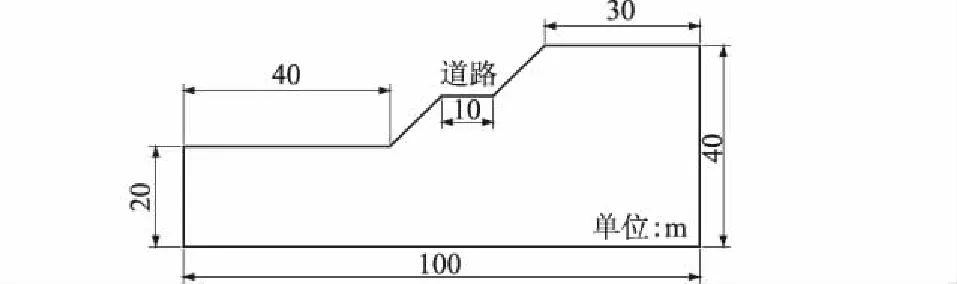
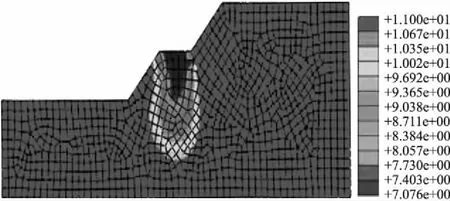
式中:N0,Na,b为表述威布尔分布的3个参数;N0是下限,也称为最小寿命参数;Na为特征寿命参数;b为描述形状参数。当N=N0时,F(N0)=0,即疲劳寿命 由于威布尔概率分布具有容易积分、均值和取值均>0等符合岩石受压破坏的统计特点[15-16],并且对于边坡而言,边坡的寿命与累积损伤因子D是相关的(D=0,边坡存活率k=1;D=1,k=0)。因此,岩质边坡微元发生破坏前后的存活率服从威布尔概率分布,公式为 (2) 对式(2)取2次自然对数可得 lnln[1-F(D)]-1=bln(D-D0)- ln(Da-D0)b。 (3) 令:y=lnln[1-F(D)]-1,x=ln(D-D0),c=ln(Da-D0)b,即可将式(3)转化为线性方程y=bx-c,利用最小二乘法进行回归求解b和c,其中,D0与N0对应,为初始损伤因子。 图1 循环荷载作用下砂岩疲劳曲线Fig.1 Fatigue curve of sandstone under cyclic loading 图2 试样损伤因子与循环次数比关系曲线Fig.2 Curve of damage factor vs. cycle ratio 疲劳试验[17]所需试样为砂岩,采自福建三明沙县,该砂岩呈灰黄色,中风化,块状结构,室内试验表明砂岩试件的单轴抗压强度为20.02 MPa,极限抗拉强度σuts为0.6 MPa。砂岩等幅疲劳试验的上限应力比Smax控制在0.8~0.9之间,下限应力比Smin恒为0.1,试验加载频率5 Hz,加载波形选用正弦波。不同上限应力比条件下的疲劳试验成果见图1,其中圆形、方形、三角形分别代表上限应力比Smax为0.8,0.85,0.9。 疲劳试验表明循环荷载下砂岩疲劳强度的Smax-Nf(疲劳寿命)关系可表示为 Smax=1.326-0.109lgNf。 (4) 文献[18]、文献[19]从损伤力学基本理论出发,利用合理的耗散势函数分析岩体疲劳损伤发展规律,建立考虑初始累积损伤因子的疲劳损伤模型,表达形式为 (5) 式中:N/Nf为循环次数比;α为材料参数。图2为试样损伤因子与循环次数比关系曲线,该曲线描述全生命周期内各阶段的损伤变量,损伤过程的积累反映岩体材料疲劳试验中产生塑性变形。式(5)的拟合结果表明初始损伤因子为0.082。 选取位于三明沙县段的边坡为研究对象,该边坡坡体材料为均质中风化砂岩,边坡的典型剖面图如图3,两段斜坡均为45°,坡高均为10 m。 图3 边坡典型剖面图Fig.3 Typical profile of slope 砂岩重度为25.8 kN/m3,弹性模量20 GPa,黏聚力380 kPa,内摩擦角33°,泊松比0.25,本构模型选用M-C准则,不考虑剪胀的影响,数值分析中考虑材料非线性和几何非线性对边坡稳定性的双重影响。交通荷载的简化可采用文献[20]的研究成果,即:通过将驶经边坡的车辆简化为朝某一方向沿道路中心线单向行驶,按Miner准则中的导致疲劳损伤等效的原则将分散在不同时段的荷载集中在某一时间段内连续完成来确定,最终将循环疲劳荷载简化为周期性简谐交通荷载,公式为 F=192sin[4π(t-0.125)]+192 。 (6) 式中:F为周期性简谐疲劳荷载(kN);t为时间(s)。 开展疲劳稳定性分析时,应先将疲劳荷载峰值384 kN全部作用于边坡路面,按有限元强度折减法求疲劳载荷第一次作用时的安全系数,计算不收敛时的安全系数为7.705;其次,可用有限元分析方法求取边坡疲劳寿命,对边坡施加峰值荷载转化后的应力,输入单位正弦波进行结构循环应力分析;英国桥梁规范(BS5400—1999)[21]建议应通过Miner破坏准则来求解交通荷载作用下桥梁的服役寿命,显然,桥梁和道路相关工程协同工作,因此,Miner准则也应适用于山区边坡的疲劳稳定性分析;最后,结合S-N曲线和Miner准则[18],即可计算边坡疲劳寿命对数,图4表明疲劳热点对应寿命为107.076(11 913 000 次)。文献[20]、文献[22]对研究区的标准疲劳日作用次数进行统计,表明该山区道路的标准疲劳日作用次数为584次,即该边坡坡脚经55.9 a(11 913 000/(584×365)=55.9 a)后可发生疲劳失稳破坏。 图4 边坡疲劳寿命对数Fig.4 Logarithmic fatigue life of slope 根据有限元强度折减法的等比例折减思路,任意折减后的中间状态岩土参数都有对应的安全系数,将初始应力状态对应的疲劳寿命作为起始值,已消耗的寿命为初始安全系数7.71时的全寿命减去中间任意应力状态对应的寿命。其中,累积损伤因子定义为已消耗寿命Ni/疲劳寿命Nf,数值计算部分成果如表2所示。 表2 数值模拟分析计算结果Table 2 Numerical simulation results 数值计算表明:①边坡稳定性分析得到的安全系数有与之对应的疲劳寿命,不再是一个恒定不变的固定值,而是具有一定的时效性;②损伤变量与材料力学强度参数具有对应关系,随着累积损伤因子D的增加,强度参数产生劣化;③车辆动荷载的动应力作用范围集中于路面下5 m左右深度。不同“结构”不需进行大修即可按其预定目的使用的时期不同,边坡工程正常设计、正常施工、正常使用和维护下所应达到的使用年限应在耐久性设计中给予体现,一旦考虑设计寿命分别为30 a和50 a时,边坡对应稳定系数为4.53和7.38;而考虑100 a设计寿命时,须进一步采取相应的工程加固措施来提高边坡结构的整体稳定性。 利用威布尔分布原理进行概率分析(即“存活率”或“破坏概率”的可靠性研究),同时考虑初始累积损伤因子的影响。通过试算,选用样本的分布函数为中位秩算法[14],中位秩Fn(ti)函数为 (7) 图5 数据拟合结果Fig.5 Result of data fitting 式中:n为所选择试验数据从小到大排序后的总数(即样本容量),选取的11组试验失效数据由小到大排列为0.199,0.244,0.263,0.377,0.436,0.617,0.752,0.814,0.881,0.934,0.989;i为经顺序统计试验失效数据后的顺序号;ti为特征寿命。根据选取的疲劳试验数据及式(3),拟合后可得图5,经转化后可获取威布尔分布函数的最终表达式,即 对式(8)进行特征点分析:当动荷载作用下边坡存活率为0.368时,对应的特征累积损伤因子为0.671;边坡存活率为0.5时,中位累积损伤因子为0.538。结合4.3小节建立边坡稳定系数与损伤因子的关系和4.4小节计算得到的边坡存活率与累积损伤因子的关系,即可反映出边坡全生命周期内的稳定系数与存活率之间的动态变化,采用式(8)进行实际计算时,应先对数值分析得出的全生命周期进行折减,即:考虑初始累积损伤因子。 图6 边坡已消耗寿命与稳定系数的关系变化趋势Fig.6 Curve of consumed life vs. safety factor of slope 图6表明:随着边坡疲劳寿命的逐渐消耗,边坡全寿命周期内的稳定系数逐渐下降;边坡在0~15 a的设计使用年限内,早期稳定系数变化比较敏感,随后的15~35 a内,稳定系数下降幅度减小而在边坡寿命后5 a,边坡具有迅速发展至破坏的特点,疲劳破坏具有突发性。具有一定节理裂隙的道路边坡,初期动荷载可加速微裂纹萌生、扩展和贯通,损伤加剧;其余较完整岩土体随着动荷载的进一步影响,岩土体中某一处应力因周围环境扰动突然升高周期较长,表现为边坡已消耗寿命与稳定系数变化具有较明显的过渡段;一旦应力向周围传播,达到损伤临界值时,边坡迅速达到其疲劳寿命,发生破坏。 图7为存活率与边坡剩余寿命和稳定系数的关系,总体上看:边坡剩余寿命和稳定系数越高,存活机率越大。当以特征累积损伤因子进行控制时,意味着边坡可存活超过36 a而不用进行整体的加固措施,但此时的稳定系数<3.7;当以中位累积损伤因子控制时,此时边坡只有剩余约25 a的寿命,稳定系数须在4.1(图7(b)中的B点)以上才能满足要求;图7中的C点为边坡处于疲劳寿命后期的存活率,安全系数为1,表现为低存活率(为0.11)。 图7 存活率与边坡剩余寿命和稳定系数的关系Fig.7 Variation of survival rate and residual life of slope against safety factor 表4为动荷载作用下山区道路边坡阶段式预警准则,边坡全生命周期变形可分为初始蠕变、稳态发展、加速发展、滑动破坏4个阶段。 表4 山区道路边坡阶段式预警准则Table 4 Staged early warning for slopes inmountainous regions 初始蠕变阶段:山区公路在0~8.5 a的运营年限内,边坡具有较强的自我稳定能力,节理裂隙的存在使得道路边坡稳定系数具有早期下降较敏感的特点;稳态发展阶段:道路边坡生命周期在8.5~46 a时,岩体应力因扰动而增加,但增加至破坏应力所需周期较长,因此边坡稳定系数缓慢变化,但边坡存活几率急剧下降;加速发展阶段:运营年限在46~55.9 a时,岩体应力迅速传播,边坡稳定系数急剧下降,直至残余存活率;滑动破坏阶段:边坡稳定系数和存活率降至最低,可随时发生失稳破坏。工程设计中应通过不断调整抗疲劳措施来加强边坡工程的耐久性,以使边坡处于稳态发展阶段,因此,定义耐久性因子λ为可用存活率(F(D)Available)与设计存活率(F(D)Design)比值,有 (9) 若考虑耐久性的设计存活率为1,可用存活率为0.6,则耐久性因子λ为0.6,显然λ<0.6时,应采取相应的抗耐久性工程措施来加强边坡稳定性。实际的可用存活率与设计存活率应根据工程特点及使用条件进行选用。 对于承受交通荷载的山区道路边坡, 应考虑交通荷载引起的岩土体劣化及共振产生的影响, 在耐久性设计中考虑耐久性因子。 上述思路正确反映了交通荷载循环作用引起岩土抗剪强度参数劣化的趋势, 但强度折减法假定稳定系数与岩土体参数劣化成正比关系, 而实际上两者间的关系远比这复杂得多, 岩土体参数的实际衰减路径值得进一步的研究。 (1)借助威布尔分布函数建立砂岩存活率与累积损伤因子(疲劳寿命)之间的关系;山区道路边坡节理裂隙发育,在其全寿命周期内稳定系数随疲劳寿命的消耗而降低,具有初期变化敏感、中间缓慢过渡和后期迅速下降的特点。边坡存活率随着剩余寿命和安全系数的减小而减小,耐久性设计可由特征累积损伤因子和中位累积损伤因子进行控制。 (2)通过量化存活率与稳定系数和累积损伤因子的关系,实现山区道路边坡在全生命周期内的阶段式预警。山区道路边坡阶段式预警准则可分为4个阶段:初始蠕变、稳态发展、加速发展、滑动破坏。动荷载作用下山区道路边坡工程设计应同时考虑抗共振和抗疲劳作用,提出的耐久性因子可实现边坡工程耐久性设计的量化,并达到从稳定性和可靠性控制边坡工程的目的。 (3)应进一步开展动荷载作用下岩土体抗剪强度参数衰减规律研究,结合文中所提边坡工程耐久性设计思路,实现工程设计到达设计使用年限要求的目的;同时,应进一步开展室内地质力学模型的疲劳测试,结合相似原理对文中所提耐久性设计思路及相关模型公式进行检验与修正。

3 疲劳试验成果
4 边坡疲劳稳定性数值分析
4.1 计算模型及参数的选取
4.2 疲劳稳定性分析方法
4.3 边坡稳定系数与损伤因子的关系

4.4 边坡存活率与累积损伤因子的关系




5 结 论

