基于叠前反演的泥页岩地层压力预测方法

李玉凤，孙 炜，何巍巍，杨云飞，章新文，严移胜

（1.中国地质大学（北京）地球物理与信息技术学院，北京100083；2.中国石化石油勘探开发研究院页岩油气富集机理与有效开发重点实验室，北京100083；3.中国石油勘探开发研究院西北分院，兰州730020；4.中国石油河南油田分公司勘探开发研究院，郑州450018）

0 引言

近年来，页岩气的勘探开发推动了美国的能源革命，带动了全球页岩气勘探开发的热潮［1-2］。作为一种战略资源，我国也开展了大量页岩油气的勘探开发工作。调研显示，国内页岩气藏主要分布在四川盆地的涪陵焦石坝、丁山、彭水、威远、长宁、昭通、富顺—永川等地区［3-6］。目前，四川盆地东部涪陵气田焦石坝地区的页岩气勘探开发取得了显著成效，已成为我国页岩气能源的重要基地［7-10］。从目前页岩气钻井揭示的情况来看，地层压力与页岩气产能呈较好的正相关关系，即高压地层往往对应着页岩气的高产能区［7-9］，但是，如何准确预测页岩气地层压力，寻找页岩气富集区，仍是进一步提高该区勘探开发的关键问题。

在地层无异常压力存在时，地下某一深度的地层压力与地表到该位置的静水柱压力相等。由于多种地质因素造成了地层压力与静水柱压力趋势线的偏离，称之为异常地层压力。一般包括2种情况，即当地层压力明显高于或低于静水柱压力时，分别称为异常高压和异常低压，且异常高压比异常低压更为多见［11-13］。

一直以来，地球物理工作者在地层压力预测方面进行了多种探索。本次研究，先探讨常规地层压力预测方法的适用性，再以川东焦石坝地区志留系龙马溪组的优质页岩为研究实例，对异常地层压力的测井响应特征进行分析，并对比新方法与传统方法的预测结果，以期验证异常地层压力识别因子的有效性和准确性。

1 地层压力预测方法

地层压力预测方法一般分为钻前地震资料预测、随钻地层压力监测及钻后测井检测等3类。在勘探阶段，主要关注的是如何利用地震资料预测异常地层压力的分布特征。国内外关于地层压力预测方法的研究已历经数十年，且主要分为等效深度法、Eaton公式法、Fillippone公式及其改进法、波阻抗反演法等4种。

（1）等效深度法

最早的地层压力预测方法由Hottman等［14］基于测井曲线提出，并由Magara［15-16］改进为可进行定量压力求取的方法，其技术思路为：先通过测井曲线建立正常压实条件下速度与深度的趋势线，再利用地震资料求取地层层速度与深度的关系，最后将两者相结合进行某一地层深度处异常地层压力的计算。

等效深度法的应用和推广一直存在争议［17］，该方法中泥岩正常压实趋势线的确定问题、速度谱求取的精度问题都会影响其实际应用效果。

（2）Eaton公式法

为了满足地层压力预测的需要，Eaton［18］和Bowers［19］利用地震速度与垂直有效应力的关系，提出了基于正常地层压实条件下，用速度变化的趋势线来求取地层压力的新方法。该方法未能得到广泛应用，其主要受以下2方面的限制：①该方法要求垂直有效应力与纵波速度呈幂指数关系，而这种假设往往不成立；②该方法要求构建的正常压实趋势线与等效深度法中的压实趋势线没有本质区别。

（3）Fillippone公式及其改进法

为了解决正常压实趋势线的问题，Fillippone［20］提出了一种新的计算方法，即在实际应用中，将测井数据和速度谱数据相结合，就可计算出地层压力数据体。该方法消除了等效深度法和Eaton公式法对正常压实速度趋势线的依赖，且能够得到地层压力的空间分布特征，因此，Fillippone方法在过去的几十年中得到了广泛的推广。为了进一步提高地层压力预测的精度，国内外学者在不同地区利用各种理论对Fillippone法进行了改进，并在与“压实”相关的异常地层压力预测中均取得了较好的应用效果［21-25］。

在实际应用中，该方法仍然存在一些不足，主要表现在地震速度体的精度问题（地震道集拾取速度谱求取的地震波层速度在纵向和横向上均不够准确）。

（4）波阻抗反演法

利用波阻抗反演来进行压力预测的主要研究思路为：①基于波阻抗反演计算有效应力的地层压力预测方法，并通过波动方程、初等弹性理论或虎克定律等的公式推导，以有效应力为中间参数，得到地层压力与纵波速度、横波速度等弹性参数的关系式，再结合叠前反演实现对地层压力数据体的计算［26-27］；②通过波阻抗反演来获取更加准确的层速度，再将层速度代入Fillippone公式中求取地层压力数据体［28］；③结合Gardner公式，先建立波阻抗与速度的关系式，然后用多种对异常压力较为敏感的地震属性来约束波阻抗反演，最后利用反演出的波阻抗计算出地层压力数据体［29］；④先利用声波测井曲线进行单井压力预测，得到单井的测井压力曲线，然后以这些压力曲线为约束，结合波阻抗反演来预测地层压力［30］。

目前，地层压力预测方法主要基于速度与异常地层压力的关系，在一定程度上能够满足异常地层压力预测的需要［31-34］，但是，上述方法主要解决的是与压实成因相关的异常地层压力预测问题，且预测精度仍有待提高。对于四川盆地焦石坝地区龙马溪组的泥页岩地层来说，欠压实作用并不是异常地层压力的主要成因［34］，导致常见的地层压力预测方法在页岩气勘探中的应用效果不够理想。

2 页岩气地层压力测井分析

2.1 测井响应特征分析

异常地层压力的形成，通常是不同地质因素的综合响应。不同成因的异常地层压力其测井曲线响应特征也不同。如，生烃产生的超压（包含高压和超高压）会使测井曲线表现出密度曲线值降低、声波时差变大等特征，而化学压实或成岩作用形成的超压，会使测井曲线表现出密度曲线增大、声波时差变化较小等特征。这为利用测井曲线进行异常压力识别并进一步进行平面推广提供了理论依据。研究中，以钻井实测地层压力数据为基础，对多种测井曲线进行超压测井响应特征分析。

钻井实测地层压力是进行地层压力预测的基础，研究区收集到的测井曲线较全，且有3口钻井的实测地层压力数据，分别为JY1井、JY 3-3 HF井和JY11-4井（表1）。

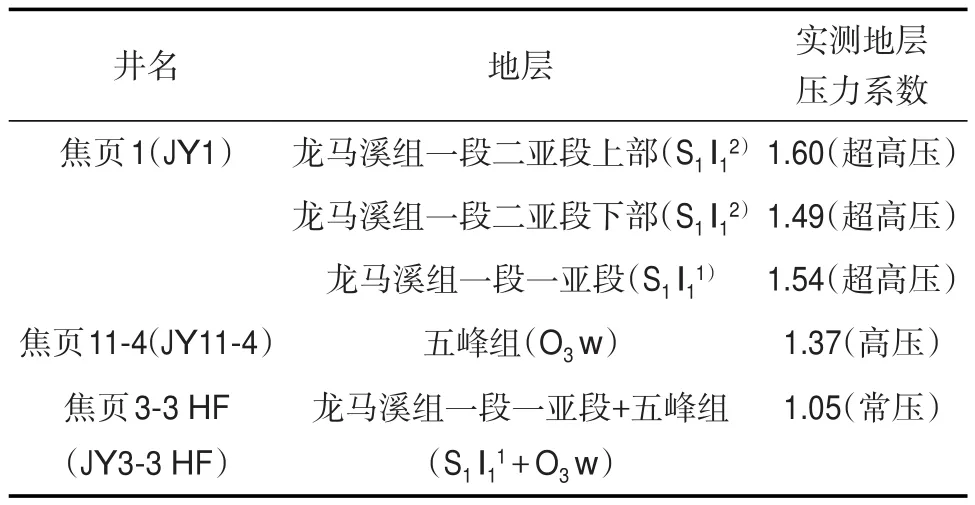
表1 焦石坝地区实测地层压力数据Table1 Measured formation pressuredata of Jiaoshiba area

对这3口井资料的测压井段进行纵波声波时差、密度、纵波阻抗、中子、自然伽马、钍铀比等多种曲线的交会分析认为：中子、自然伽马、钍铀比等曲线均无法有效区分超压和常压，而对于纵波声波时差、密度和纵波阻抗测井曲线，JY11-4井以及JY1井的超压段地层表现出高声波时差、中低密度、低波阻抗等高含气量的测井响应特征；JY3-3 HF井由于位于断层附近，气体大量散失，其常压段地层表现出低声波时差、中高密度、高波阻抗等低含气量的测井响应特征（图1）。由图1可以看出，密度曲线和声波时差曲线对超压和常压均有一定的区分，具体表现为：密度值大于2.47 g/cm3时为高压和常压，而密度值小于2.47 g/cm3时为超压；声波时差低于235μs/m时为常压，而声波时差高于235μs/m时为超压和高压。由于纵波阻抗是速度与密度的乘积，且密度、速度与地层压力均表现出相似的负相关关系（超压特征为密度和速度均低），因此，研究中选用纵波阻抗测井曲线来进行研究区常压段与超压段的区分。

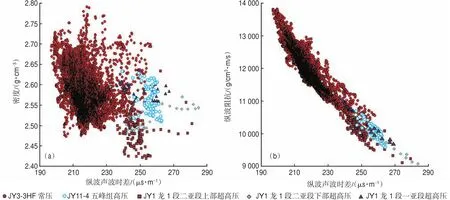
图1 超压和常压段密度与纵波声波时差（a）、纵波阻抗与纵波声波时差（b）交会图Fig.1 Cross plots of density and P-wave acoustic transit time（a），P-wave impedance and P-wave acoustic transit time（b）in overpressure and normal-pressure zones

为进一步分析页岩气异常压力发育段的测井响应特征，研究中以压力系数1.4为界限，将超压段划分为大于1.4的超高压段以及低于1.4的高压段，并引入横波声波时差曲线，分析超高压段以及高压段的测井曲线响应特征（图2）。

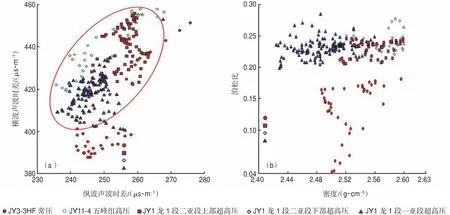
图2 高压和超高压段横波声波时差与纵波声波时差（a）、泊松比与密度（b）交会图Fig.2 Cross plots of S-wave acoustic transit time and P-wave acoustic transit time（a），Poisson’s ratio and density（b）in overpressure and ultra-high pressure zones

从图2（a）可以看出：红色圆圈内数据主要为JY1井的超高压段，而JY11-4井高压段绝大部分位于红色圆圈之外。此外，在图2（b）中，JY11-4高压段为低泊松比，而JY1井超高压段为高泊松比。结合泊松比的定义可知，当泥页岩地层存在超压，且受到垂向压力引起一定的横向应变时，地层压力越大，对应的垂向应变越小。

2.2 异常地层压力识别因子的构建

根据前述异常地层压力测井响应特征分析结果，并基于以下2点来构建能够有效识别页岩气异常地层压力的新参数：①新构建的参数应与地层压力系数呈正相关关系；②新参数的值域应与地层压力系数的值域在同一范围内。新参数构建思路如下：①在超压与常压的测井分析中，纵波阻抗与地层压力呈负相关关系，且经过井上数据试算，对纵波阻抗进行平方运算处理后，能进一步提高纵波阻抗与地层压力的相关性，因此，将纵波阻抗的平方置于新参数的分母位置；②在高压与超高压的测井分析中，泊松比与超压呈正相关关系，因此，将泊松比置于新参数的分子位置；③考虑泊松比的值域为0～0.5（无量纲），泥页岩纵波阻抗的数值一般在10 000 g/cm3∙m/s附近，而实测地层压力系数的值域一般为0.9～2.0，因此，在新参数的分子部分乘以一个常数1010，从而使新参数的值域与实测地层压力系数的值域相同，以便对后续两者相关系数的统计分析。

最终，基于上述思考构建出一个新的异常压力识别因子 API（Abnormal Pressure Indicator），该参数具体形式如下：

式中：υ 为泊松比；Imp为纵波阻抗，g/cm3∙m/s；API为构建出的异常地层压力识别因子。

页岩气超压最直接的特征是由于气体大量聚集造成的纵波速度、密度、纵波阻抗显著降低，这与该区的钻井实际情况相吻合；在泥页岩超压地层中，岩石的应力应变特征决定着异常地层压力的细节变化。

在实际应用中，可以通过叠前弹性波阻抗反演来进行纵波阻抗、泊松比的求取，从而计算出异常压力识别因子数据体，并进一步进行异常地层压力分布特征的描述。在利用叠前或叠后地震反演求取密度数据体时，预测结果往往误差较大，这会影响构建的异常压力识别因子的预测精度，但是，本次研究区目的层为焦石坝龙马溪组龙一段一亚段的一套发育非常稳定的泥页岩，在实际研究中，目的层段密度反演的效果非常好［35-37］。因此，密度反演的误差问题并不会影响新方法压力预测的精度。

3 泥页岩地层压力预测

3.1 叠前弹性波阻抗反演

一直以来，Zoeppritz方程被广泛用于描述地震入射波、反射波和透射波在穿过岩层界面时的变化特征，但其形式过于复杂，学者们往往通过各种近似来对其进行求解［38-42］。Connolly［42］定义了一种随入射角变化的新阻抗参数（弹性波阻抗Elastic Impe-dacne），为使其满足叠后反射系数的计算公式，Connolly 引入 Aki等［39］对上述 Zoeppritz方程近似后得到的反射系数解析公式，最终得到的弹性波阻抗如下：

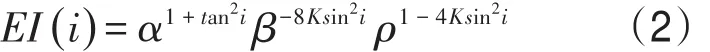
式中：EI(i)为随入射角变化的弹性波阻抗，g/cm3∙m/s；i为入射角，（º）；α 为纵波速度，m/s；β 为横波速度，m/s；ρ为密度，g/cm3；K（K=β2/α2）为常数，取相邻层的平均值。

研究中，收集的地震数据为经过叠前时间偏移的 CRP（Common Reflection Point）道集数据及对应的叠前时间偏移速度数据，相关的叠前反演均基于上述数据展开，研究中具体的工作流程如下［43］：①分析叠前CRP道集的偏移距范围，根据钻井分层给出目的层深度，确定出最大有效偏移距；②利用叠前时间偏移速度数据，在最大有效偏移距范围内，确定合理的入射角划分方案，并进行远、中、近的入射角叠加；③计算井上不同入射角的弹性波阻抗曲线，并分别进行与远、中、近入射角叠加数据体的井震标定，确定时深关系及反演子波；④利用叠后反演方法，分别计算出不同入射角的远、中、近弹性波阻抗数据体；⑤利用远、中、近弹性波阻抗数据体，结合弹性波阻抗公式建立方程组并求解，计算出最终的纵波速度、横波速度以及密度数据体，利用这3个参数数据体可以进行泊松比、波阻抗等弹性参数的求取。

3.2 异常地层压力识别因子法压力预测

焦石坝地区位于四川盆地东南部，页岩气主力产层为龙马溪组的一套优质泥页岩，工区主体构造特征为北东走向的箱状背斜，总体表现为南宽北窄、中部宽缓，背斜两侧发育多条逆断层，区内地层压力难以求准。

研究中通过叠前弹性波阻抗反演分别计算出纵波阻抗和泊松比数据体，结合式（1），即可求得研究区的异常压力识别因子数据体。对该数据体沿龙马溪组底界选取合适时窗，对龙马溪组一段一亚段的异常压力识别因子进行平面图绘制（图3）。

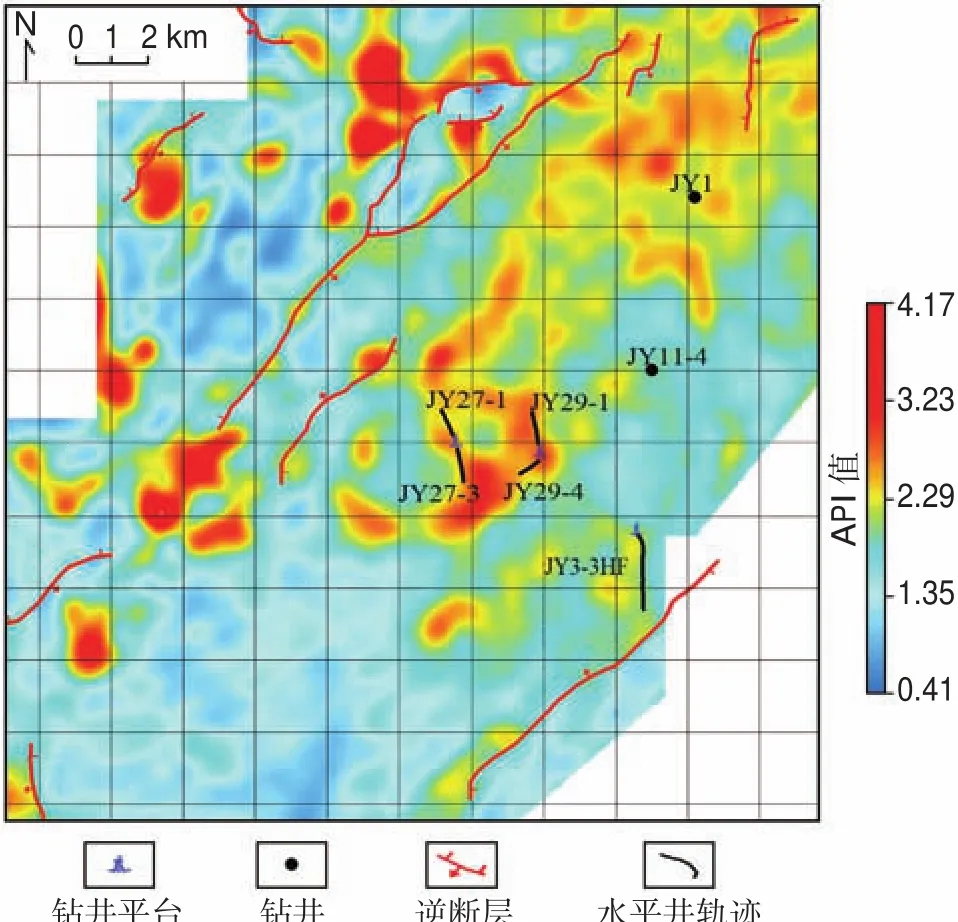
图3 焦石坝地区龙马溪组一段一亚段异常压力识别因子平面图Fig.3 Map of abnormal pressure identification factor of the first member of Longmaxi Formation in Jiaoshiba area

如图3所示，预测出的异常超压区主要分布在研究区的中部和东北部。本次研究收集了部分钻井龙马溪组一段一亚段的实测压力系数值，进一步将异常压力识别因子API的数值与实测地层压力值进行对比（表2）。

表2 异常压力识别因子与实测地层压力系数对比Table 2 Abnormal pressure factor and measured formation pressure coefficient

将表2中的实测压力系数以及异常压力识别因子数据按序列进行成图（图4）。从图4可以看出：异常压力识别因子与实测地层压力值整体趋势表现出较好的一致性。

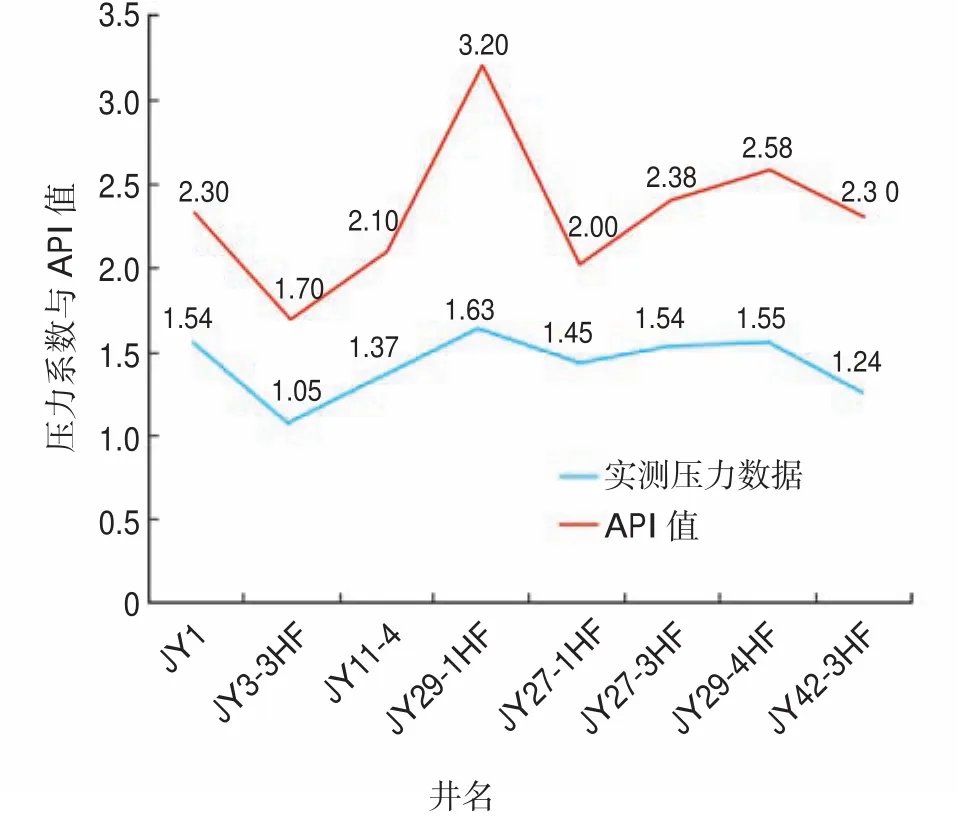
图4 异常压力识别因子与实测地层压力系数趋势对比Fig.4 Comparison of abnormal pressure factor and measured formation pressure coefficient

将两组数据进行拟合（图5），得出地层压力计算公式，即

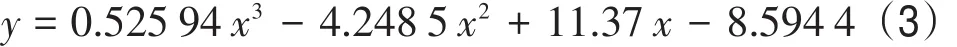
式中：x为异常压力识别因子的数值；y为根据关系式计算出的地层压力系数。

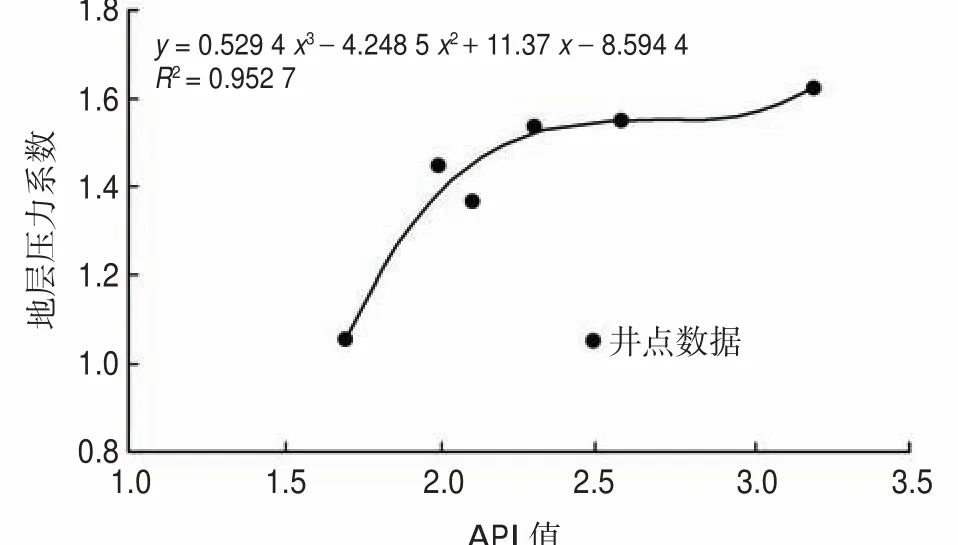
图5 实测地层压力与异常压力识别因子关系拟合Fig.5 Fitting of measured formation pressure coefficient and abnormal pressure factor

从图5可以看出：两组数据的相关性较好，为0.952 7。可以利用式（3）对异常压力识别因子的数值进行转换，求取异常压力识别因子法对应的地层压力系数平面图［图 6（a）］。

3.3 方法对比与分析

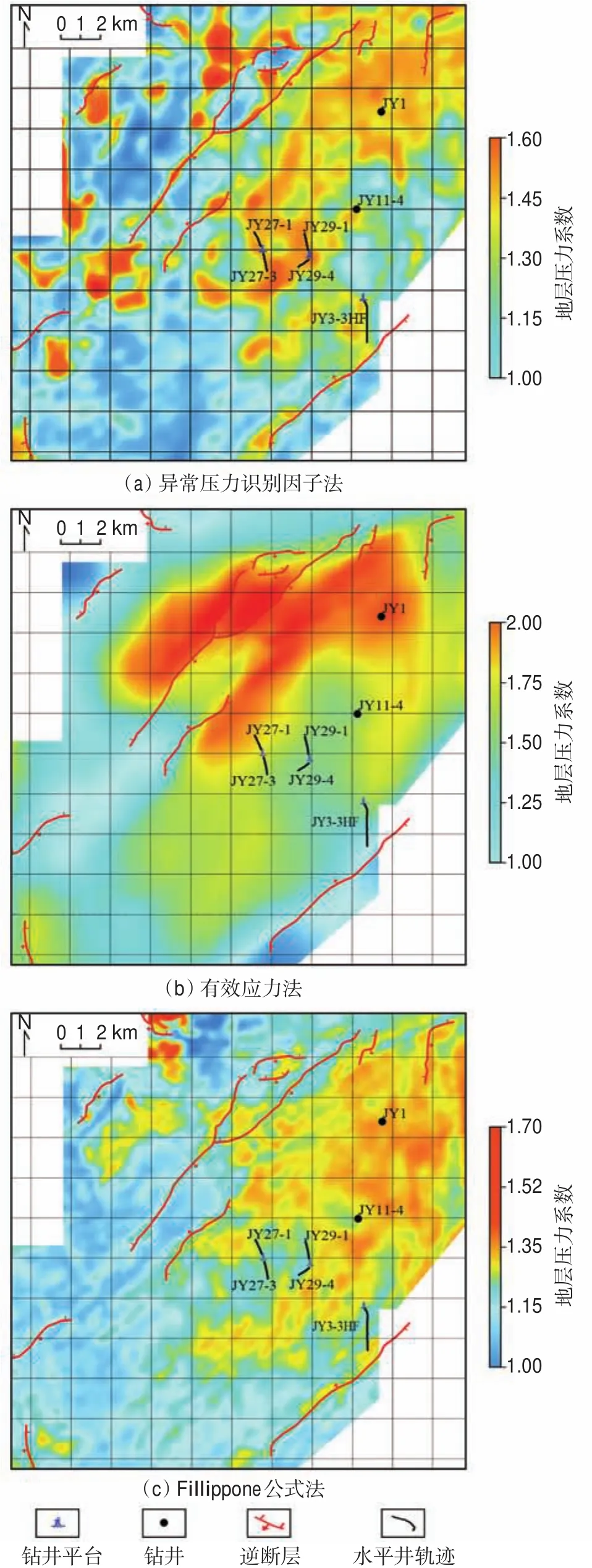
图6 3种方法预测的地层压力系数对比Fig.6 Comparison of formation pressure coefficients predicted by three methods

为对比不同地层压力预测方法预测结果的准确性，将研究中采用的新方法异常压力识别因子法与传统的Fillippone公式法、基于波阻抗反演计算有效应力的地层压力预测方法（以下简称有效应力法）的预测结果进行对比（图6）。其中，有效应力法的参数选取，根据三轴应力实验及钻井实钻参数确定，具体计算公式见文献［27-28］。

从3种方法预测的总体趋势来看，超压主要分布在研究区的中部和东北部。为进一步对比这3种方法预测出的超压平面分布特征的准确性，进行了各方法预测结果在井点位置与单井实测地层压力系数的误差分析（表3）。

结合图6和表3的分析结果，可以看出：①从平面图的分辨率来看，Fillippone公式法预测出的超压发育带呈大片连续分布，分辨率较低，而有效应力法与异常压力识别因子法的预测结果比Fillippone公式法的预测结果分辨率高；②从平面分布特征来看，3种方法的整体趋势较为一致，预测的超压均主要分布在研究区的中部和东北部地区，但Fillippone公式预测出的超压范围更大；③从预测精度的误差分析来看，Fillippone公式法误差较大，平均误差为20.10%，单井最大误差为43.81%；④有效应力法在未与井进行参数拟合的情况下，平均误差为13.14%，单井最大误差为20.25%，该预测结果已经具备一定的可靠性；⑤异常地层压力因子识别法的预测精度最高，平均误差为5.42%，单井最大误差为11.66%。

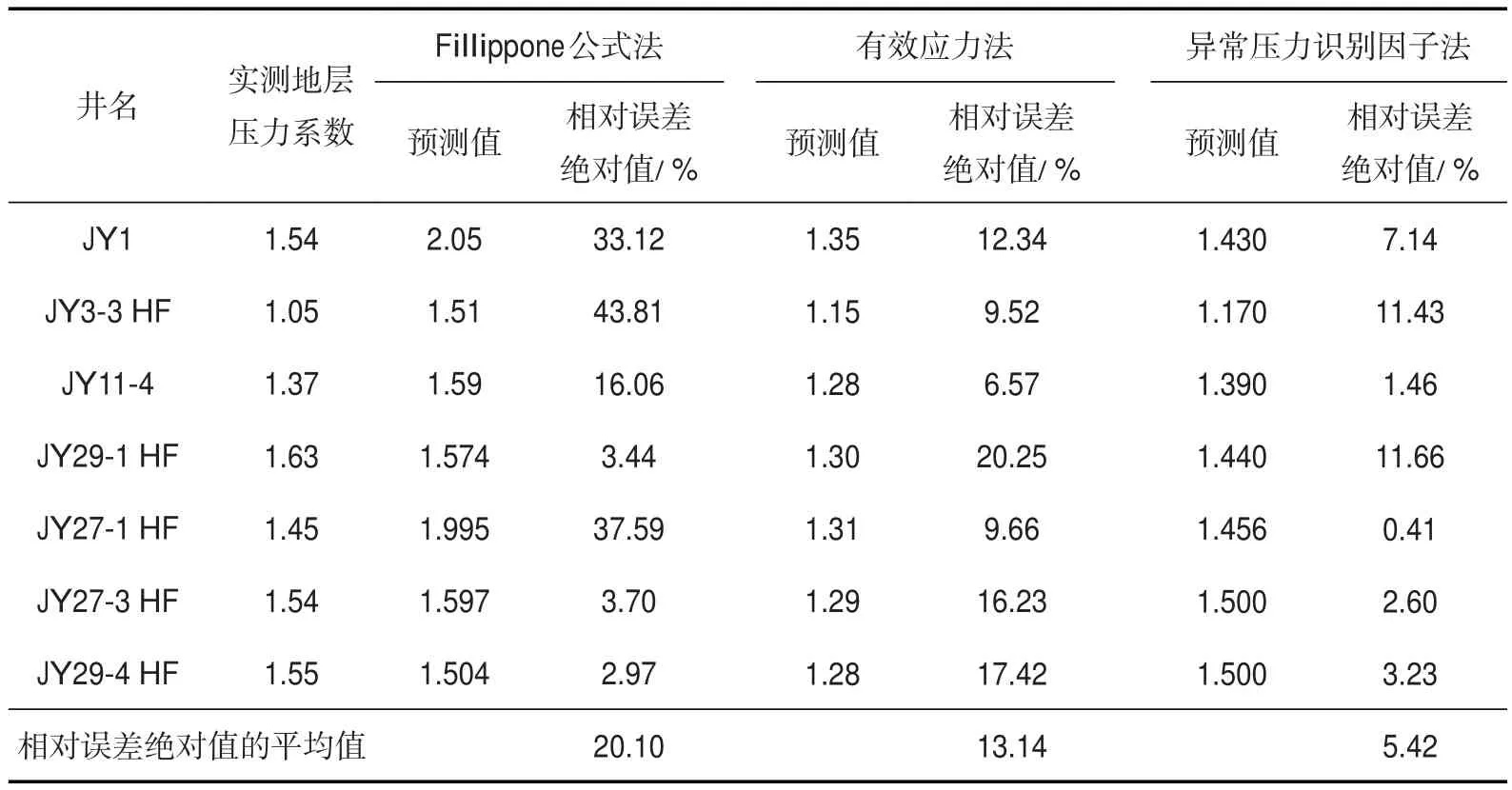
表3 3种方法预测结果与井点地层压力系数误差分析Table3 Prediction resultsof threemethodsand error analysisof formation pressurecoefficient

4 结论

（1）焦石坝地区的纵波阻抗能够有效区分泥页岩地层中的常压和超压（包含高压和超高压），而泊松比可以进一步区分泥页岩地层的高压和超高压。

（2）基于测井分析提出的新的泥页岩压力预测方法，即异常地层压力识别因子法，能够较为准确地预测地层压力的分布特征，且在分辨率及精确度上均比传统的Fillippone公式法更高，基于波阻抗反演计算有效应力的地层压力预测方法具有一定的推广价值。

（3）异常地层压力识别因子法仍存在一定的局限性，即需要充足的井资料（实测压力数据、横波时差测井曲线等）以确保井上分析的准确性，而当实测地层压力数据不足时，其应用效果有待于进一步验证。