基于自回归模型表面肌电信号检测肌肉疲劳研究

杨 铮 王立玲 马 东

河北大学电子信息工程学院，河北省数字医疗工程重点实验室，河北 保定 071002)

引言

非平稳信号是一种分布参数随时间变化的随机信号，如生物医学工程中的脑电信号与表面肌电信号(surface electromyography，sEMG)。在医疗领域，表面肌电信号的有效处理不仅为患者提供肌肉疲劳诊断依据，而且提供了有效的治疗手段[1-2]。因传统特征值表征肌肉疲劳时变化不明显、反映不够灵敏，很有可能在肌肉已经发生疲劳时而未检测出疲劳，造成肌肉损伤。因此，如何在肌肉受到损伤之前检测出疲劳，防止由普通性肌肉疲劳进一步恶化发展成肌肉损伤已成为当今一个值得研究问题。时变系数建模方法是处理非平稳信号典型方法。已广泛应用于多种非平稳信号处理领域。

时变系统的参数辨识方法主要有自适应算法和基函数展开法。自适应算法中常见有经典递推最小二乘法、最小均方差算法和卡尔曼滤波法等。自适应算法是针对信号具有弱平稳特性时，时变系统参数变化较慢，其可以对时变系统参数进行准确辨识。否则，辨识参数会因其收敛性的缺陷，导致时变系统参数的结果估计产生延迟[3]。而基函数展开法是针对信号具有较强非平稳特性时，其可以对时变系数进行有效估计[4]。时变系统参数表示为一组已知基函数的线性加权组合[5]，将时变系统建模问题变成了关于基函数的时不变参数辨识问题，通过对时不变参数的辨识进而得到时变系数。而基函数选择常见有傅里叶基、勒让德多项式和小波基，不同基函数具有不同的逼近特性，其中傅里叶基和勒让德基函数适用于有效辨识变化缓慢的时变系数，而小波基函数适用于有效辨识变化剧烈的时变系数。国外 Chon 等及国内刘洪涛等根据勒让德多项式具有灵活的逼近特性对时变系数进行展开并取得了较好的逼近效果[6-7]。径向基函数(radial basis function，RBF)具有中心对称特性、良好的局部特性、多尺度特性、多分辨率特性，已广泛应用于系统辨识领域[8]。

研究人员通过大量的实验揭示，伴随着肌肉的疲劳，功率谱一般由高频向低频漂移，中位频率(median frequency，MF)和平均功率频率(mean power frequency，MPF)的值都呈下降趋势，与肌肉的疲劳成相关性[9]。在实际应用中，MPF指标对肌肉活动状态和功能状况的敏感性强于MF指标[10]。但相关研究表明，频域中影响表面肌电信号频谱变化的因素主要与神经传导速率、动作电位持续时间有关。在动态收缩至疲劳过程中肌肉温度会升高，温度升高会影响表面肌电信号频谱高频成分增加，导致MPF、MF变化不明显[11-12]。这些现象是由神经传导速率变化导致的[13]。但上述传统特征值是基于短时傅里叶分析的，在检测肌肉疲劳时，采样时间较长、实时性和分辨率较差，是传统方法在评估疲劳领域中制约其应用的一个关键问题。因此，如何有效进行实时快速检测及评估肌肉疲劳，已成为当今一个值得研究问题。

1 方法

1.1 实验对象

受试者为10例健康男性，测试者均无上肢肌肉劳损病史，身体质量指数正常，实验前24 h内均无参加任何剧烈活动。每位受试者在实验前都接受实验通知，并签署知情同意书，进行试验动作培训；实验地点在河北省数字医疗工程重点实验室。

1.2 实验过程

实验前，实验室调整温度27℃，将受试者首饰物品取下，电极片贴放于右上肢肱二头肌中部。每组受试者右手心向上，上臂与身体平行，小臂与上臂肘角度为90°，手持1.5 kg哑铃开始做等长收缩运动直至受试者主观感觉肌肉疲劳不能继续为止，采集并记录右上肢肱二头肌疲劳前期、后期数据。由于每位受试者年龄、个体之间差异较大，所以要求哑铃重量、电极贴放位置等必须一致。

实验设备与材料：实验开始前，准备实验设备与材料，包括计算机、无线表面肌电采集系统(包含DTS肌电传感器1个、DTS桌面接受盒、双电极夹1个、5 V DC充电线、Mini USB数据线、弹性固定带1条)、电极片2片、酒精、棉签、受试者信息。

采用品牌为美国NORAXON、型号为表面肌电信号采集系统、版本为MR3.6软件。利用无线表面肌电信号传感器，使用一次性Ag/Agcl电极片，设定时间常数为0.05 s、采样频率为1 500 Hz，根据肌肉模型粘贴一次性电极片，电极片间距为20 mm。

1.3 信号预处理

1.3.1滤波

由于表面肌电信号比较微弱，有用信号分布在0～500 Hz频率范围之间，主要能量部分分布在50～150 Hz频率范围之间。由体表电极检测到的表面肌电信号主要含有工频干扰(50 Hz)、基线漂移和心电干扰(5～20 Hz)等，这些噪声会严重影响表面肌电信号质量。为了增强表面肌电信号中的有效成分，抑制噪声和伪迹，噪声的有效消除对肌电信号的后续处理至关重要。采用巴特沃斯20～500 Hz带通滤波器消除基线漂移和心电干扰，巴特沃斯带阻滤波器消除50 Hz工频干扰[14]。

1.3.2归一化

不同受试者肌肉活性存在差异，为了能够统一比较不同参数特征值对疲劳表征效果，需要对表面肌电信号进行归一化操作。

1.4 自回归模型及时变参数辨识

本试验中自回归模型(autoregressive，AR)描述是一种“短时平稳”随机过程，该随机过程在该时刻的观察值xn与该时刻之前的观测值xn-i存在相关性。设p阶参数自回归模型计算公式为

(1)

式中：ai(n)是自回归系数，也是AR(p)模型参数；n=1，2，…，N，N为采样数据长度；en是平稳白噪声过程；xn是观察值，xn-i是观测序列值。

由于采集肌电设备采样频率为1 500 Hz，因此时变系统参数变化太快，自适应算法的收敛性存在缺陷，因此研究采用基函数展开式方法。基函数展开式方法对时变系统进行辨识，将时变系数ai(n)表示为一组基函数的线性组合[15-16]，即

(2)

式中，aij为展开式时不变系数，fj(n)为基函数，m为基函数扩展维数。

将式(2)代入式(1)，得

(3)

令A=[a11a12…a1m…ap1ap2…apm]T，B=[B1B2…Bp]，X=[x1x2…xN]。

(4)

则式(3)可改写为

X=BA+e

(5)

利用基函数展开式将时变模型式(1)中原来p个时变系数的识别问题转化为p×m个定常参数的识别，即将原来非平稳过程的参数识别转化为一个线性时不变系统的辨识。模型表示为矩阵形式后，由最小二乘法解出时不变参数A的估计值，即

(6)

1.5 频域分析

频域分析是从频率角度来分析表面肌电信号的特征，方法是将时域信号经过短时傅里叶转换后得到表面肌电信号的频谱或功率谱。频域分析常用分析参数有MPF、MF[17-18]。

由于MPF、MF都是基于短时傅里叶分析，其时间和分辨率都是固定的，然而对于表面肌电信号来讲，频谱分布范围较宽时，难以找到一个合适的时间窗来分析，即其时间和频率分辨率较低。

(7)

(8)

式中，pi为单位功率谱的估计值(功率谱密度)，N为1/2信号采样点数。

1.6 参数变化率

通过对比分析3种方法的疲劳指标疲劳前、后的变化率(change rate，CR)来确定哪个特征参数值指标对于肌肉疲劳反应灵敏性更高，进一步说明哪种方法适合用来表征肌肉疲劳。疲劳前、后相关特征参数值变化率定义[19]为

CR=(yi+M-yi)/yi×100%

(9)

式中，yi为疲劳前值，yi+M为疲劳后值。

经过计算，疲劳前、后表面肌电信号的MPF分别为209.34、149.30 Hz，MF分别为132.95、104.15 Hz。由式(9)求得的MPF变化率为-28.68%，MF变化率为-21.66%。

由于MPF、MF是基于短时傅里叶原理，采样时间较长、实时性和分辨率较差。为了能够比较3种方法对肌肉疲劳的敏感性，以下MPF、MF特征值都是基于N=15 000点(t=10 s)数据长度计算。基于时变AR模型要求采样时间短、对时间反应迅速等特点，应用时变参数AR模型处理疲劳前、后的前N=150点(t=0.1 s)数据，可得到相应的时变参数。经过计算，疲劳前、后表面肌电信号的ARC1分别为-2.25、-3.09。由式(9)求得的ARC1变化率为37.39%。

时变自回归模型法是以最小均方误差拟合角度对表面肌电信号进行分析，克服了经典谱估计频率分辨率低和方差性能差缺点。从相对于短时傅里叶变换分析来看，其克服了传统提取频域参数要求表面肌电信号采样时间足够长的问题。以采样频率1 500 Hz、时间窗512点举例说明，计算MPF、MF参数时最短数据也需要512/1 500≈0.34 s>0.1 s。

1.7 Legendre基函数维数选择

实验采用AR参数模型提取特征参数，模型阶数一般取p=4～6，取Legendre基，Legendre基函数(Legendre basis function，LBF)的最佳维数由相关指数求得[20-22]。相关指数越大，说明模型拟合效果就越好，有

(10)

1.8 统计学分析

采用Ecel 2013软件数据分析模块。采用双尾t检验分析的方法来分析各个参数特征值对疲劳反应灵敏性效果的统计学差异性，即分析各个参数特征值对肌肉疲劳程度表征效果的统计学差异性。

变化率数据统计步骤：要先进行F检验，F检验又叫方差齐性检验。在双样本t检验中要用到F检验，F检验的目的是确定采用双样本等方差t检验还是采用双样本异方差t检验。如果F检验单尾P值的2倍大于0.05，说明两者方差之间无显著性差异，则采用双样本等方差t检验。否则，选择双样本异方差t检验。

2 结果

图1为一典型受试者肱二头肌的表面肌电信号图，可看出肌肉在疲劳前、后表面肌电信号幅度有增大趋势，反映了肌肉收缩至疲劳时参加活动的运动单位数量增加，体现为肌肉疲劳过程中表面肌电信号幅度增大。

图1 表面肌电图。(a)疲劳前期；(b)疲劳后期Fig.1 The sEMG of biceps brachi muscle. (a) The early stage of fatigue; (b) The later stage of fatigue

图2为一典型受试者的基于基函数展开式法估计6阶AR模型得到的相关指数L随基函数维数变化，Legendre基函数最佳维数由式(10)求得。由图2可以看出，基函数维数m≥4时参数辨识效果波动不大，趋于稳定。大量实验验证，p=6、m=7时的参数辨识效果最佳。

图2 相关指数随基函数维数变化；(a)疲劳前；(b)疲劳后Fig.2 The correlation index changing with LBF dimension;(a)Pre-fatigue;(b)Post-fatigue

图3为一典型受试者基于Legendre展开式法时变参数辨识结果。可以看出，基于Legendre展开式法因具有良好的局部特性，能够更好地跟踪信号，辨识结果比较平滑，尤其是在波峰和波谷处没有参数突变位置的现象。因此，基于Legendre展开式法具有理想的辨识效果。

表1 各受试者疲劳特征值及其变化率(疲劳前后)Tab.1 The characteristic value and change rate of the subjects(pre-fatigue and post-fatigue)

注：a:ARC1 vs MPF，P>0.05;b:ARC1 vs MF，P>0.05。

Note:a：ARC1 vs MPF,P<0.05;b：ARC1 vs MF，P<0.05.

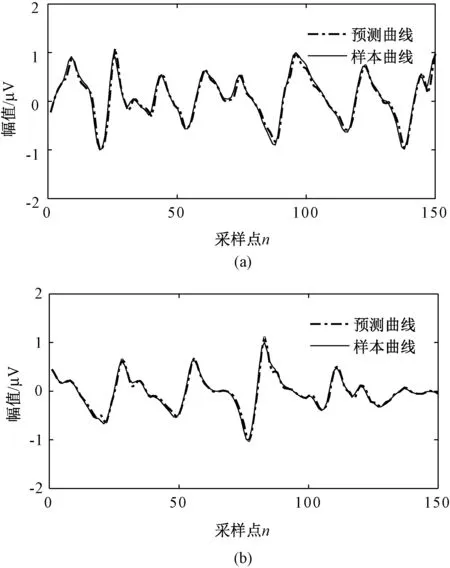
图3 基于Legendre展开式法时变参数辨识结果。(a)疲劳前；(b)疲劳后Fig.3 Identification results of AR parameters by LBF expansion method.(a)Pre-fatigue;(b)Post-fatigue

表1为10组受试者疲劳前、疲劳后相关特征值及其变化率大小。实验结果得到10组时变参数，以每组AR模型第一个参数(ARC1)最重要，它直接体现当前时刻与上一时刻关系，是肌肉状态随时间变化的最直接量，每阶AR参数都是随时间点变化。计算所估计信号0.1 s时间段内ARC1为评价肌肉疲劳状态指标。计算所估计信号10 s时间段内MPPF、MF为评价肌肉疲劳状态指标。

从疲劳前、疲劳后各特征参数变化趋势上来看，ARC1、MPF、MF三者均呈现出变小趋势，从疲劳前、后各特征参数变化率上来看，ARC1的变化率较高。采用AR模型克服了MF、MPF要求表面肌电信号采样时间足够长问题。将10例受试者疲劳前、后MPF、MF、ARC1变化率作为疲劳指标，变化率进行统计分析，通过计算变化率均值和标准差分别为25.68%±2.03%、22.80%±2.19%、34.33%±2.41%。由于ARC1与MPF和ARC1与MF两者两两之间存在显著性差异，且分别显著高于MPF和MF，表明采用ARC1参数指标跟踪肌肉疲劳具有较高分辨率灵敏度。

3 讨论

运动性疲劳学说有衰竭学说、堵塞学说、内环境失调学说、保护性抑制学说、突变理论、自由基损伤学说等。Boyas等认为，肌肉疲劳主要是由于发力过程中逐渐出现钙离子运动扰动、磷酸盐等代谢物积累、肌细胞三磷酸腺苷减少等因素，导致动作电位传导变化和肌纤维收缩力量下降[23]。Pavlov等认为，肌肉疲劳是大脑皮层保护性抑制结果。随着疲劳加深，为了减少消耗，中枢神经系统发放频率降低，导致运动神经元发放冲动频率随之减小。中枢神经对运动神经元控制精度也降低，导致了运动单位间活动同步化程度增强，体现为肌肉疲劳过程中ARC1、MPF、MF下降。

ARC1针对表面肌电信号的非平稳特性，采用AR模型对表面肌电信号进行分析，对短时间内表面肌电信号的肌肉疲劳迅速做出高灵敏性判定。由于ARC1在评估肌肉疲劳时具有灵敏性高、检测肌肉疲劳时间短等优点，因此ARC1应用于肌肉疲劳领域可以达到及时发现、及时防止由普通性肌肉疲劳进一步恶化成肌肉损伤的效果，以免对个人、家庭及社会带来巨大的经济负担。

影响MPF、MF在疲劳过程中变化不明显的影响因素有肌肉发力方式、肌肉表面温度。在早期相关领域研究中，Tesch等研究发现，肌肉以动态收缩发力方式使肌肉发生疲劳过程中MPF、MF变化不明显[24]。Petrofsky等研究发现，肌肉收缩至疲劳过程中肌肉表面温度会逐渐上升，这样会增加表面肌电信号频谱高频成分，从而导致MPF、MF变化不明显[25]。除了肌肉发力方式、肌肉表面温度这两个影响因素外，还有肌肉收缩强度也会使MPF、MF在疲劳过程中变化不明显。吕飞等研究发现，在不同运动强度(30%、55%、80% MVC)下，MPF与MF的下降率具有明显的负荷强度效应[26]。然而，当运动强度过低(<20% MVC)时，理论上将不会产生MPF、MF的任何变化[27]。

采用短时傅里叶变换的方法，虽然能够得到对疲劳敏感的参数来表征肌肉疲劳，但短时傅里叶变换在时间和频率上分辨率低。当分析表面肌电信号频谱分布范围较宽时，时间窗选择就成了难题。时间窗选择不佳，便会影响到对疲劳敏感的参数表征肌肉疲劳效果[28]。时变自回归模型不受窗函数的影响这一优点已经被相关学者应用到分析表面肌电信号领域。在早期相关研究中，Merletti等研究发现，自回归模型系数随着肌肉疲劳程度加深，会出现逐渐变小趋势[29]。Chang等研究发现自回归模型系数的平方随着肌肉疲劳程度加深会出现逐渐变小趋势[30]。

本研究采用Legendre基函数，对线性时变系统在白噪声激励下时变系统参数进行展开，并利用相关指数来选择Legendre基函数最佳维数。通过展开肌肉疲劳实验研究，各特征参数对肌肉疲劳表征效果方面进行分析。通过实验将ARC1与传统频域参数MPF、MF进行对比研究， 证明ARC1在评估肌肉疲劳领域的可行性及有效性。

4 结论

本研究应用Legendre基函数展开式方法将线性非平稳过程辨识问题转化为线性时不变系统辨识问题。对10例受试者表面肌电信号进行特征提取，短时间内ARC1变化率作为评估肌肉疲劳敏感性指标，实验证明，比MPF、MF对疲劳反应的敏感性更高，从而有将细微特征信息放大，使不明显的特征信息变明显的效果。

通过表面肌电信号对肌肉疲劳检测，不仅能够更好表征肌肉疲劳变化程度，而且具有时间短和敏感性高等优点，可应用于在线实时检测肌肉疲劳，为上肢肌肉劳损评估、康复治疗及人体工效学的研究提供一个可靠分析工具。时变参数辨识问题一直是学术界研究难点，从10例受试者ARC1灵敏性均高于MPF和MF灵敏性可知，该研究方法具有适用性特性。为了进一步验证及巩固上述结果正确性及实用性，除了大量仿真验证该实验具有时间短、敏感性高等优点之外，在接下来的研究中，后期仍需要进行大量实验加以验证，从而进一步提高其在肌肉疲劳判定等领域中的实用价值。