中气旋与强对流风暴相关参数的演变关系

张 军，闫丽飞，侯谨毅



中气旋与强对流风暴相关参数的演变关系

张 军，闫丽飞，侯谨毅

(天津大学电气自动化与信息工程学院，天津 300072)

强对流天气对社会公众的危害极大，强对流风暴内部的中气旋通常与灾害天气相关．为了预测强对流天气的发生时间，研究了中气旋参数与强对流风暴参数的相关关系．针对强对流风暴参数与中气旋参数之间的变化规律，引入了时间序列关联规则的挖掘方法．收集了天津塘沽雷达站的24个包含中气旋的强对流风暴案例，使用强对流风暴参数和中气旋参数的时间序列来描述案例集合，并使用典型变量分析算法将归一化的时间序列数据降维，考虑到序列间的变化趋势和局部关键点的影响，提取单调性特征和局部极值点特征对时间序列符号化表示，将同一时间段内的符号组成事务集，使用Eclat算法发现频繁项集；并且类比于学习器的性能度量，提出评估两类数据变化规律的正比率与反比率概念．实验结果显示，强对流风暴参数与中气旋参数之间存在显著的相关性，其第1对典型变量的相关系数大于0.5；在支持度为0.05～0.30下，Eclat算法的运行时间小于0.7ms，内存占用小于121KB，均优于Apriori算法和FP-growth算法；强对流风暴参数与中气旋参数之间的正比率大于0.7，直观地反映出强对流风暴参数与中气旋参数之间变化趋势的相似程度，且再次验证了频繁项集的正确性．该研究为利用中气旋数据预测强对流天气的变化趋势与发生时间提供了理论依据．

强对流风暴；中气旋；关联规则挖掘；时间序列

中国气象局将强对流天气定义为冰雹(落地直径大于2cm)、龙卷(除水龙卷之外)、直线型雷暴大风(瞬时速度大于17m/s)以及对流性暴雨等天气灾害．这些灾害不仅每年造成数亿元的经济损失，而且对人民的生产生活造成严重影响．产生强对流天气的天气系统在气象领域被称为强对流风暴，其具有时间空间尺度小、局部地区性强、持续时间较短等特征[1].中气旋是一个与强对流风暴的上升气流和背面下沉气流密切相关的小尺度涡旋，它与重要的灾害天气有着很大的关系．研究强对流风暴参数与中气旋参数之间的关联关系，可以在强对流风暴的演化早期发现强对流天气的预警，减少社会的损失．

目前，关于中气旋和强对流天气相关性的研究已经有很多．比如2007年方翀等[2]发现中气旋的顶高、底高和最强切变与灾害性天气的相关关系，为大风、雷雨的预报提供了较为精确的依据．2012年吴芳芳等[3]发现带有高顶高低的中气旋对流风暴易形成冰雹，带有底低与直径小的中气旋对流风暴易形成龙卷，中气旋的切边发生剧变、底高与顶高下降易产生雷雨大风的对流风暴．2017年郑艳等[4]发现具有较低的底高中气旋有助于龙卷的发生．2018年高晓梅等[5]发现中气旋的厚度、最大切边、持续时间与天气的强烈程度有着密切的关系．文献[6]通过分析强对流天气的具体案例，明确了中气旋与强对流灾害天气的关系．然而，根据以往这些相关性的研究，不能够准确地判断强对流天气何时发生．在本文中，为了能够利用中气旋预测强对流天气的发生时间，研究了中气旋演变过程与强对流风暴结构演化的相关关系．

本文将时间序列关联规则的挖掘方法应用于强对流风暴与中气旋参数变化规律的研究中．关联规则挖掘是从大量数据集中挖掘出数据之间的关联关系．Agrawal等[7]首次提出了关联规则挖掘的概念；之后他提出了分类规则挖掘算法，即Apriori算法．为节省生成频繁模式的时间，Han等[8]提出了一种经典关联规则挖掘算法，即FP-growth算法，但是该算法需要对数据进行两次扫描．为减少扫描数据库的次数，Zaki[9]在2000年提出了Eclat算法，该算法使用垂直数据库表示法，采用深度优先搜索，只需扫描一次数据库，可以在数据集之间高效且方便地找到频繁项目集．Das等[10]首次提出将关联规则应用于时间序列中，率先提出了关于单个时间序列的关联规则挖掘．时间序列的关联性挖掘重点在于将时间序列转换为事务集，Lin等[11]建议使用符号聚合近似(SAX)将相等的时间段内的数据进行离散化，但该方法只考虑到了数据的大小特征．Xue等[12]选择单调性与Knee Point表示数据，从而降低数据的维度，使用改进的Apriori算法可以发现特殊模式和关联规则，也推动了对于时间序列关联挖掘的发展．

为了能够使用时间序列关联挖掘的方法研究强风暴和中气旋参数的关联关系，本文收集了天津气象台塘沽站2005—2010年伴随着中气旋的强对流风暴的数据．首先，使用典型相关分析来降低强对流风暴与中气旋数据的维度，得到两者的第1对典型变量，并且根据相关系数定量地分析出强对流风暴与中气旋的联系．之后，为了能够具体分析强对流风暴与中气旋的参数变化趋势的相关性，通过提取第1对典型变量的单调特征和局部极值的特征，对时间序列进行符号化表示，将相同时间段内的符号组成一组事务集，利用Eclat算法找到频繁项集，从频繁项集中定量地分析出强对流风暴和中气旋的参数变化趋势. 另外，类比于学习器的性能度量方法，本文提出一种评估两类数据变化规律的性能度量，用于验证频繁项集的正确性．

1 方法描述

图1所示的流程展示了如何采用时间序列关联规则分析方法来研究中气旋与强对流风暴相关参数之间的关联关系．该流程图主要由4部分构成：中气旋与强对流风暴参数的时间序列表示、时间序列预处理、事务集的生成和频繁项集的挖掘．下面依次给出每个部分的详细描述．

1.1 时间序列表示

时间序列是指同一统计指标下的数值按照时间顺序排列而成的数据集合，记为

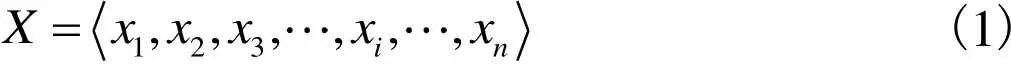
   (1)

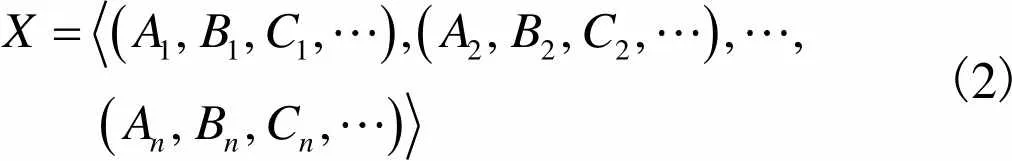
   (2)

图1 系统流程

1.2 时间序列预处理

在使用时间序列表示中气旋与强对流风暴的相关参数之后，为避免不同特征参数的量纲对数据分析结果的影响，对同一特征参数进行了归一化处理，之后进一步对数据进行了降维处理．

降维是数据预处理的一种通用手段，对分析至关重要．常用的降维算法有主成分分析(PCA)、线性判别分析(LDA)等，但是单纯地对每组数据变量进行降维处理会影响两组数据之间的相关关系[13]．所以本文采用典型相关分析方法(CAA)对两组数据进行综合降维，以期使用少量的综合变量来反映两组数据之间的相关性．

Hotelling[14]在1936年提出了典型相关分析，它是一种研究两组变量之间线性相关的统计分析方法．它将多维变量进行加权求和形成综合变量，通过少数的综合变量反映原始变量间的相关性．它的基本思想是首先在每组变量中找出变量的线性组合，使该线性组合具有最大相关性，然后再找出第2对线性组合，分别与第1对线性组合互不相关，而第2对线性组合自身具有最大的相关性，如此继续下去，提取完毕两组变量之间的相关性为止．

   (3)

   (4)

   ，(5)

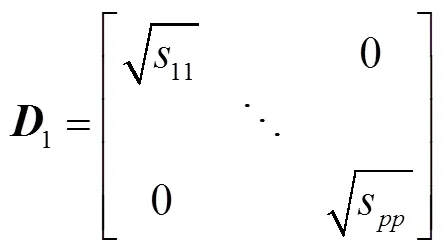
   (6)

则可得协方差矩阵分别为

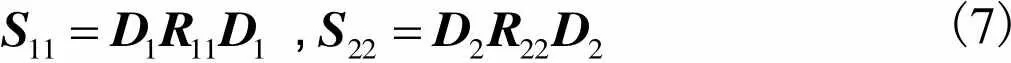
   ，(7)

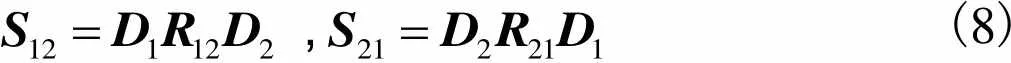
   ，(8)

   ，(9)

   (10)

   (11)

   (12)

显然可得

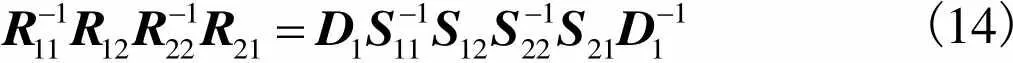
   (14)

又因为

   (15)

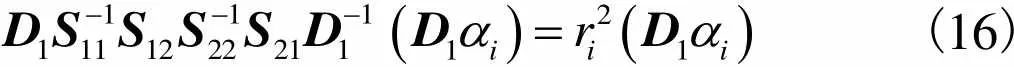
   (16)

可以得出

   (17)

   (18)

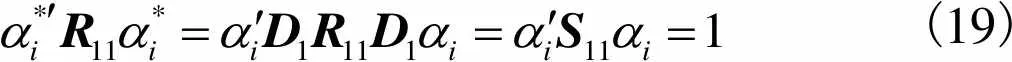
   (19)

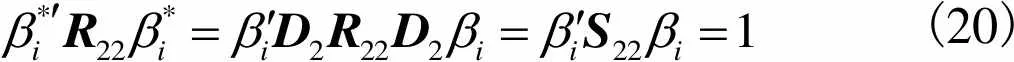
   (20)

   ：，：(21)

则典型相关系数的似然比统计量为

   (22)

建立统计量为

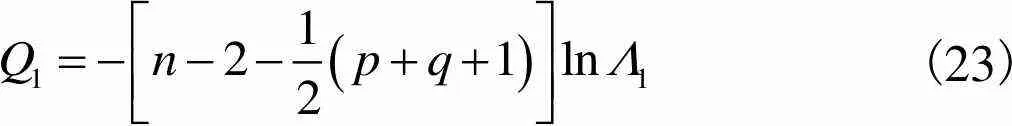
   (23)

1.3 事务集生成

前文所得的中气旋与强对流风暴的时间序列不能直接用于关联规则挖掘，需要将时间序列符号化表示，转化为不同符号表示的符号序列，对于符号化的序列，需要组成事务集之后才能进行关联规则挖  掘[15]．本文提取时间序列相邻时间段内的单调性特征与局部极值点特征来符号化表示时间序列，这样不仅考虑了数据的变化趋势，还考虑了数据间的弯曲幅度信息．

1.3.1 单调特征

   (24)

相对斜率表示单位时间间隔内的涨跌幅度，其公式为

   (25)

1.3.2 局部极值特征

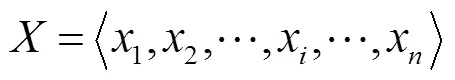
图2 局部极值点示例

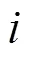
表1 符号的定义

Tab.1 Definitions of symbols

注：下标“1”代表该数据为强对流风暴序列，“2”代表该数据为中气旋序列．

1.3.3 组成事务集

利用序列符号化描述方法，为序列中的每段时间间隔分配一个符号，每个序列都可以表示成一系列符号．为了防止引入局部极值点而导致两个序列的长度不同．在寻找局部极值点时，如果一个序列此时刻为局部极值点，而另外一个序列在此时刻不是极值点，则使用符号“o”表示．符号化表示的时间序列示例如图3所示．

图3 符号化表示的时间序列示例

将每个过程的两个符号序列在同一个时间段内的符号组成一个事务，使用一个唯一的标识符对应，即事务ID．全部过程的所有事务组成事务集．合并后的事务集如表2所示．

表2 时间序列数据形成的事务集

Tab.2 Setof transactions formed by time series data

1.4 基于Eclat的频繁项集算法

1.4.1 频繁项集的基本理论

   (26)

为得到频繁项集，需要合理确定支持度阈值．挖掘频繁项集的任务就是找出大于支持度阈值的所有项集[16]．

1.4.2 Eclat算法挖掘频繁项集

Eclat算法的思想是深度优先搜索，通过倒排将事务数据中的项作为关键字，每一项对应的事务ID作为值．包含项的所有事务集合称为项的Tidset．该算法是通过集合的交集运算来计算项目集的支持[17].

2 实验设计与结果分析

2.1 数据来源

数据来源于天津气象台塘沽雷达站，选取2005—2011年天津市由强对流风暴而引发的冰雹、暴雨等严重灾害的数据．其中一共含有41个完整的过程，有27个过程检测到中气旋的存在．从中提取出24个完整的包含中气旋在内的强对流风暴过程，每个过程不少于1h，且每个过程中中气旋数据与强对流风暴数据无缺失．将每个过程中强对流风暴与中气旋的数据按照时间先后顺序存放在一个文本文件中.

2.2 参数的选取

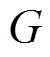
   (27)

强对流风暴和中气旋的多维时间序列可分别表示为

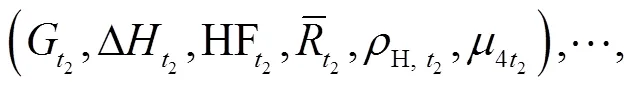
(28)

     (29)

2.3 典型变量分析

对强对流风暴与中气旋的参数进行典型变量分析，提取出24个过程的第1对典型变量，得到第1对典型变量的相关系数在各个范围内的频率与比例，如表3所示．

表3 第1对典型变量的相关系数取值范围

Tab.3 Correlation coefficient range of the first pair of typical variables

相关系数取值范围频数比例 0.5～0.620.083 0.6～0.730.120 0.7～0.830.083 0.8～0.920.125 0.9～1.0140.583

从表3可以看出，24个过程中第1对典型变量的相关系数均在0.5之上，且0.7之上的达到89%，可以认为强对流风暴与中气旋的典型变量之间存在显著相关性．

2.4 Eclat算法挖掘频繁项集

表4 最小支持度为30%的频繁模式

Tab.4 Frequent-itemsets with min_sup＝30%

为了说明算法的优越性，本文在不同支持度下比较了Apriori算法、FP-growth算法与Eclat算法的运行时间与内存占用，结果如图4与图5所示．

图4 不同支持度阈值下3种算法运行时间的比较

从图4可以看出，Eclat算法在不同支持度下的所需的运行时间最短，可以达到近乎实时运行的效果．这是因为Eclat算法只需对数据集进行1次扫描，极大地减少了对搜索空间的搜寻时间，而且符号化的事务集有很高的重复率，数据量较小，使用Eclat算法时执行交叉操作所需的时间非常短．

图5 不同支持度阈值下3种算法内存占用的比较

从图5可以看出，在不同的支持度阈值下，FP-growth算法的内存占用多，大于Apriori算法的内存占用，但Eclat算法所占的内存始终是最小的．

2.5 变化规律的性能度量

   (30)

   (31)

表5 两组数据变化趋势关系

Tab.5 Change trend relation of two sets of data

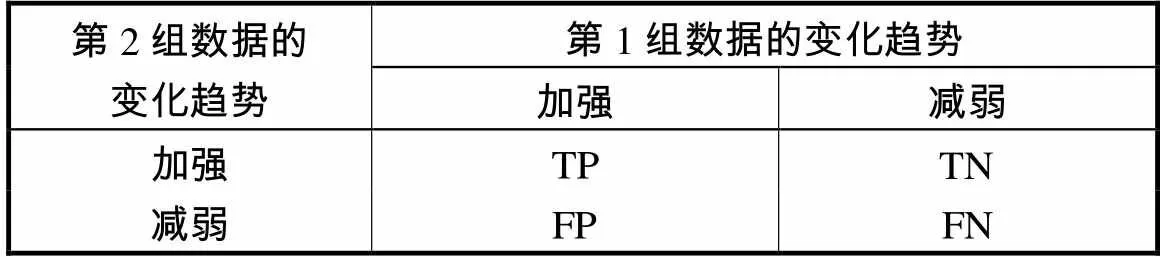
第2组数据的变化趋势第1组数据的变化趋势 加强减弱 加强 减弱

强对流风暴和中气旋参数单调性特征的关系如表6所示．

表6 单调性特征的关系

Tab.6 Relation of monotonicity characteristic

强对流风暴的变化趋势中气旋的变化趋势 2a，2c2b 1a，1c9744 1b32106

表7 局部极值关系

Tab.7 Relation of local extreme

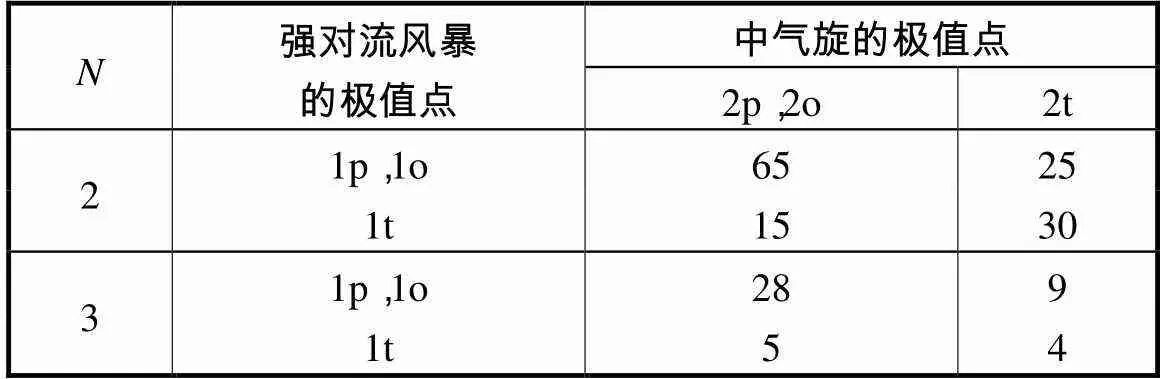
N强对流风暴的极值点中气旋的极值点 2p，2o2t 21p，1o6525 1t1530 31p，1o289 1t54

3 结 论

(1)应用典型相关分析方法发现强对流风暴与中气旋的标准化参数的第1对典型变量之间存在显著的相关性．

(2)使用Eclat算法对符号化后序列进行频繁项目集的挖掘，得到的频繁项集显示强对流风暴与中气旋参数的变化趋势呈现很大的一致性．

(3)相比于Apriori算法和FP-growth算法，Eclat算法需要的运行时间更少，占用内存更低．

(4)本文提出了一种性能度量的方法，根据其正比率与反比率直观地反映出两组时间序列数据之间变化趋势相似程度，验证了所得到的频繁项集的正 确性．

［1］ 程 浩. 中尺度气旋识别与三维重建[D]. 天津：天津大学电气与自动化学院，2007.

Cheng Hao. Mesoscale Cyclone Identification and 3D Reconstruction[D]. Tianjin：School of Electrical and Automation，Tianjin University，2007(in Chinese).

［2］ 方 翀，郑媛媛. 新一代天气雷达中气旋产品特征值统计和个例分析[J]. 气象，2007，33(11)：16-20.

Fang Chong，Zheng Yuanyuan. The analysis of mesocyclone product from the Doppler weather radar[J]. Meteorological Monthly，2007，33(11)：16-20(in Chinese).

［3］ 吴芳芳，俞小鼎，张志刚，等. 对流风暴内中气旋特征与强烈天气[J]. 气象，2012，38(11)：1330-1338.

Wu Fangfang，Yu Xiaoding，Zhang Zhigang，et al. The characteristics of the mesocyclone and severe weather associated with convective storms[J]. Meteorological Monthly，2012，38(11)：1330-1338(in Chinese).

［4］ 郑 艳，俞小鼎，任福民，等. 海南一次超级单体引发的强烈龙卷过程观测分析[J]. 气象，2017，43(6)：675-685.

Zheng Yan，Yu Xiaoding，Ren Fumin，et al. Analysis on a severe tornado process in Hainan triggered by supercell[J]. Meteorological Monthly，2017，43(6)：675-685(in Chinese).

［5］ 高晓梅，孙雪峰，秦瑜蓬，等. 山东一次强对流天气的环境条件和对流风暴特征[J]. 干旱气象，2018，36(3)：447-455．

Gao Xiaomei，Sun Xuefeng，Qin Yupeng，et al. Environmental conditions and convective storm features of a severe convective weather process in Shandong Province[J]. Journal of Arid Meteorology，2018，36(3)：447-455(in Chinese).

［6］ 张 艳. 基于雷达图像的中气旋的识别及超折射回波的滤除[D]. 天津：天津大学电气与自动化学院，2009.

Zhang Yan. Identification of Mesocyclones Based on Radar Images and Filtering out of Super Reflection Echoes[D]. Tianjin：School of Electrical and Automation，Tianjin University，2009(in Chinese).

［7］ Agrawal R，Srikant R. Fast algorithms for mining association rules in large databases[J]. Computer Engineering & Applications，2000，15(6)：619-624.

［8］ Han J，Pei J，Yin Y. Mining frequent patterns without candidate generation[J]. ACM SIGMOD Record，2000，29(2)：1-12.

［9］ Zaki M J. Scalable algorithms for association mining[J]. IEEE Trans on Knowledge and Data Engineering，2000，12(3)：372-390.

［10］ Das G，Lin K I，Mannila H，et al. Rule discovery from time series[C]//Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining. Mcnlo Park，USA，1998：16-22.

［11］ Lin J，Keogh E，Lonardi S，et al. A symbolic representation of time series，with implications for streaming algorithms[C]//ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery. New York，USA，2003：2-11.

［12］ Xue R，Zhang T，Chen D，et al. Sensor time series association rule discovery based on modified discretization method[C]// IEEE International Conference on Computer Communication and the Internet. San Fran-cisco，CA，USA，2016：196-202.

［13］ Guo Y，Ding X，Liu C，et al. Sufficient canonical correlation analysis[J]. IEEE Transactions on Image Processing，2016，25(6)：2610-2619.

［14］ Hotelling H. Relations between two sets of variates[J]. Biometrika，1936，28：321-377.

［15］ 曾海泉. 时间序列挖掘与相似性查找技术研究[D]. 上海：复旦大学信息科学与工程学院，2003.

Zeng Haiquan. Research on Mining and Similarity Searching in Time Series Data Base[D]. Shanghai: School of Information Science and Technology，Fudan University，2003(in Chinese).

［16］ Aggarwal C C，Sun Z，Yu P S. Fast Algorithms for online generation of profile association rules[J]. IEEE Trans on Knowledge and Data Engineering，2015，14(5)：1017-1028.

［17］ 陈培恩．关联规则Eclat算法改进研究[D].重庆：重庆大学计算机学院，2010．

Chen Pei’en. Improving Research on Association Rules Eclat Algorithm[D]. Chongqing：School of Computer Science，Chongqing University，2010(in Chinese).

［18］ Zaki M J. Scalable algorithms for association mining[J]. IEEE Trans on Knowledge and Data Engineering，2000，12(3)：372-390.

(责任编辑：孙立华)

Evolution Relationship Between Parameters of Mesocyclone and Severe Convective Storm

Zhang Jun，YanLifei，HouJinyi

(School of Electrical and Information Engineering，Tianjin University，Tianjin 300072，China)

Severe convective weathers are extremely harmful to the public. The mesocyclone inside a severe convective storm is usually related to disaster weathers. To predict the occurrence time of severe convective weathers，the correlations between the parameters of mesocyclones and those of severe convective storms were studied. Moreover，a method for mining time series association rules was introduced in order to evaluate the variation law between severe convective storm parameters and mesocyclone parameters. Twenty-four severe convective storm cases involving mesocyclones in the Tianjin Tanggu radar station were collected. The case set was described by a time series of severe convective storm parameters and mesocyclone parameters，and a variable analysis algorithm was used to reduce the normalized time series data. Considering the trend of the variation between sequences and the influence of local key points，the monotonic features and local extremum features were extracted to symbolize the time series. The symbols in the same period were composed into a transaction set，and the frequent itemsets were found using the Eclat algorithm. Furthermore，a performance metrics method that reflects the similarity of the trends between the two sets of time series data according to positive ratio and inverse ratio is proposed to evaluate the variation law of two sets of data. Experimental results show that there is a significant correlation between the severe convective storm parameters and the mesocyclone parameters. The correlation coefficient of the first pair of typical variables is higher than 0.5. Under the support degree of 0.05—0.30，the running time of the Eclat algorithm is less than 0.7ms，and the memory occupancy is less than 121KB，which are better than those of both Apriori algorithm and FP-growth algorithm；the positive ratio between the severe convective storm parameters and the mesocyclone parameters is greater than 0.7，which reflects the similarity degree between the severe convective storm and the mesocyclone parameters and verifies the correctness of the frequent itemsets. This study provides a theoretical basis for predicting the trend and occurrence time of severe convective weathers using mesocyclone data.

severe convective storm；mesocyclone；association rule mining；time series

10.11784/tdxbz201807023

P447

A

0493-2137(2019)03-0277-08

2018-07-14；

2018-10-11.

张 军（1964—  ），男，博士，副教授，zhangjun@tju.edu.cn.

侯谨毅，houjinyi@tju.edu.cn.

天津市青年科学基金资助项目(2016120024002432)．

the Youth Science Fund Project of Tianjin，China(No. 2016120024002432).