串联输水明渠PID多指标自适应算法及仿真研究

叶雯雯，管光华，李一鸣，钟 乐

(1.武汉大学 水资源与水利水电工程科学国家重点实验室，湖北 武汉 430072；2.长江勘测规划设计研究院，湖北 武汉 430010；3.中建水务环保有限公司，北京 100070)

0 引 言

渠道自动控制是指根据渠道中传感器测得的参数、操作条件和控制目标，在没有人直接参与的情况下，利用外加的控制器，来操作节制闸，控制渠道中水位流量在一定目标状态。与传统的渠道就地人工控制相比，渠道自动控制具有响应迅速、调度灵活、控制精度高、供水质量高、节约水资源、及时应对突发事故等优点。从经济发展、节水环保等角度考虑，研究和发展渠道自动化是十分必要的。在渠道自动控制研究中，控制算法是核心，许多算法虽然已经提出，但目前仍难以应用于实际工程。目前实际工程中应用最广的PID算法依然有许多弊端，例如：PID算法参数整定的复杂性、对环境的敏感性。渠系控制固有难题也未能解决，例如：高度非线性、时变性问题。

渠道自动化科学发展至今已有一百多年历史，其控制算法从提出到目前为止，一共经历了经典控制理论阶段、现代控制理论阶段与智能控制理论阶段。经典控制理论阶段是由20世纪70年代后提出的一系列经典控制算法组成，主要研究单输入单输出的系统问题。其中，目前渠道自动控制中应用最广的比例积分加微分(PID)类控制算法在此阶段产生。PID类控制算法涵盖范围广泛，包括美国垦务局提出的EL-FLO、EL-FLO+RESET、P+PR 算法，到PI、PID控制算法等等。现代控制理论阶段发展于20世纪90年代左右，是以经典控制理论以及状态空间模型为基础，主要研究渠系系统中多输入、多输出、非线性、高精度等问题。主要研究课题为最优控制，并不断向大系统理论发展。包括1998年Malaterre[1]研究的渠道线性二次最优控制算法，Clemmens[2]等设计的最优下游控制算法和耦合水位差控制算法。20世纪末到21世纪初，随着人工智能计算机技术不断完善，智能算法在渠道控制领域得到应用，基于此产生了一系列先进的控制算法，如预测控制，自适应控制及模糊控制等，如2004年Wahlin[3]基于ID 简化模型导出的状态空间模型，2013年Hashemy[4]等研究的利用水库作为在线调蓄的算法，但这些算法尚处研究阶段，且皆为固定的控制器结构与参数，对于输水渠道系统诸如糙率、闸门流量系数等参数存在时变性的特点难以适应。

国内渠系自动化控制研究起步较国外晚。1997年王长德[5]针对下游常水位闸门提出了渠系运行的水流动态过程及其数学模型。次年王长德[6]在倒虹吸P+PR算法的研究基础上，提出多渠段串联渠系的P+PR算法，并结合渠道闸门同步操作技术，提出等体积控制模型。2003年范杰[7]将模糊控制理论与传统PID控制算法相结合。2005年管光华[8]将渠道系统的最小实现矩阵转化为一个由线性矩阵不等式约束的凸优化问题，研究多渠段鲁棒控制器。同年王长德[9]针对模糊控制器在渠系系统控制中动静态性能不佳的问题设计分层模糊控制器。2007年韩延成等[10]利用CMAC神经网络原理提出渠系自适应控制模型，并通过引黄济青工程进行仿真，同时又根据RBF人工神经网络原理[11]研究了下游常水位自适应渠道输水，并建立了RBF网络整定PID输水控制调节器。到2008年管光华[12]针对多渠段多输入多输出模型状态空间的不确定性的来源分类分析并进行了定量描述。同年管光华[13]又以南水北调为背景分析了长渠系稳态恒定流解法与非恒定流解法差异及对控制方式的影响。2011年管光华[14]将耦合水位差控制系统应用于美国中亚利桑那工程中，仿真结果显示控制系统采用耦合水位差算法具有明显的调节优势。2012年刘国强[15]针对冰期渠道长距离输水问题，提出了大型渠系中冰期渠道输水过渡模式。2015年崔巍[16]阐明了明渠渠池蓄量与节制闸闸前水位之间的单值对应关系,并在此基础上提出一套通过动态调节渠池蓄量,实现闸前常水位运行的控制算法。同年吴辉明[17]基于南水北调中线工程设计了蓄量补偿前馈策略与水位流量反馈控制模式。2017年曹玉升[18]对输水调度控制策略进行了改进,提出了基于流量变化、水位变幅相耦合的实时调度控制策略。

当前渠系自动化控制大多局限于常规PID控制。针对常规PID算法存在的问题，本文结合自适应控制和经典PID控制，提出了一种基于性能指标的自适应PID控制算法，并比选出合适的性能指标参数，通过控制器参数与性能指标的函数关系，提出自适应规则，根据该规则在线调节PID控制器的主要参数Kp、Ki值，并通过对某大型调水工程输水渠道系统干渠串联渠系进行建模仿真，旨在提高系统控制性能，解决经典PID算法随外界环境变化而控制性能降低的问题。

1 经典PID控制

目前渠道控制大多采用比例(P)控制器或者比例积分(PI)控制器，完整的比例积分加微分(PID)反馈控制数学模型为:

(1)

式中:Kp,ti,td分别为比例系数、积分时间和微分时间；e(t)为不同时间段控制量的差值。

将式(1)离散化得到位置式PID控制表达式：

(2)

式中：T为积分时间之差；U(k)为控制输出，由于位置式调节在执行环节无法避免固定位差的影响，因而产生了增量式PID控制：

ΔU(k)=KpΔe(k)+Kie(k)+Kd[Δe(k)-Δe(k-1)]

(3)

式中：Δe(k)=e(k)-e(k-1)，k为采样序列；e(k)为第k次采样时刻输入的偏差值；Ki为积分系数；Kd为微分系数。

上述PID控制方法虽然结构简单、容易实现，但该方法中3个参数不能根据环境变化进行自适应调整，而且由于渠道系统时变不确定性、高度非线性等特点，传统PID 控制满足不了高精度和高时效性的控制要求。

2 自适应PID算法设计

2.1 自适应控制

自适应控制系统定义尚不明确，目前有两个广泛认同的定义[19]：

定义① (Gibson，1962年)：一个自适应控制系统应提供被控对象当前状态的连续信息，即辨识对象；将当前系统性能与期望性能或某种最优指标进行比较，在此基础上做出决策，对控制器进行实时修正，使得系统趋向期望性能或趋于最优状态。

定义② (Landau，1974年)：一个自适应系统，应利用可调系统的各种输入—输出信息来度量某个性能指标，然后将测量得出的性能指标与期望指标进行比较，由自适应机构来修正控制器的参数或产生一个辅助信号，以使系统接近规定的性能指标并保持。

随着计算机技术、微电子技术的发展，自适应控制在过程控制中具有一定运用，如在航空航天领域，美国宇航局的Gupta Pramod等[20]利用神经网络自适应控制器对巡航导弹控制进行实时监测和评估，在航空领域取得重大发展。在航海领域，廖健等[21]针对无阀电液伺服操舵装置参数慢时变的非线性控制，提出一种基于单神经元的自适应PID控制方案，在提高操舵装置的动态特性以及适应参数变化方面由于常规PID算法。

2.2 自适应PID控制模型

自适应PID控制器基本可分为两类：①参数自适应控制器----依据被控过程模型参数估计设计控制器参数，包括极点配置自适应PID控制器和基于二次型性能指标的自适应PID控制器。②非参数自适应控制器----依据某些过程参数制定自适应规则进行整定，包括模糊自适应PID控制、神经网络自适应PID控制和专家自适应PID控制器对于渠道这种时变不确定性、强非线性系统，为了获得更好的控制效果，需要设计一种智能的自适应控制方法对PID的3个参数进行在线调整，本文采用参数自适应算法中基于性能指标的自适应PID控制器并加以修改。仿真模型如图1。

图1 基于性能指标的自适应PID控制图

在该模型中，首先确定一组能正常运行的PID控制参数，渠系系统在设定的工况下进行常规PID控制仿真，仿真结束后被控对象输出性能指标值，与目标性能指标比较，然后比较器输出信号传入自适应机构，自适应机构进行决策，通过设定自适应规则对PID控制器进行参数整定，使其达到较优的控制状态。

2.3 自适应控制指标

出于衡量渠道控制性能及测试控制算法优劣的需要，1998年ASCE渠道控制算法工作组提出了一个标准的测试算例[22]，并在算例中给出了衡量控制效果的一系列系统性能指：最大绝对误差(MAE)、稳态误差(StE)、绝对值误差积分(IAE)、绝对流量变化积分(IAQ)、绝对闸门开度积分(IAW)、水位误差平方积分(ISE)、流量误差平方积分(ISQ)、最大水位降速(MAXDROP)。

本文从中挑选出绝对流量变化积分(IAQ)、绝对闸门开度积分(IAW)、绝对值误差积分(IAE)加上超调量(OVR)和衰减率(DAM)5个直接反映闸门动作情况的指标，拟作为自适应控制的参考指标。

(1) 绝对流量变化积分(IAQ)。

(4)

式中：Qt为t时刻的过闸流量；t1、t2为流量开始变化时间、结束变化时间；Qt1、Qt2分别为初始流量与最终流量。

IAQ指标反映了控制器对渠道过闸流量的控制能力，指标值越小表示实际流量与目标流量越接近。

(2) 绝对闸门开度积分(IAW)。

(5)

式中：Wt为t时刻闸门开度。IAW指标与IAQ指标在表达式上相似，两类指标反映了过闸流量与闸门开度的关系。但是，渠系系统设有闸门死区与水位死区，渠系过闸流量与水位波动变化相比于闸门开度而言更为剧烈。

(3) 绝对值误差积分(IAE)。

(6)

式中：yt为t时刻水位；Δt为控制采样时间步长，离散系统为定值；T为系统仿真计算总时间步长。

IAE指标反映了水位波动过程，是系统实际水位与目标水位的偏差积累。IAE指标越小，闸门的开启次数会相应减少，降低开启速度也会下降，系统能快速达到稳定状态。选择较好的IAE指标有助于优选出整个过渡过程较为平缓的控制器参数。

(4) 超调量(OVR)与衰减率(DAM)。超调量表示被调参数动态偏离给定值的最大程度，为输出响应的最大值与稳态值之差与稳态值的百分比。衰减率是指每经过一个波动周期，被调量波动幅值减少的百分数，为同方向的两个相邻波的前一个波幅减去后一个波幅之差与前一个波幅的比值。

本文采用MATLAB软件对单渠段PID控制器各参数进行模拟仿真，得到在不同Kp、Ki值的条件下对应的3个性能指标值，并找出Kp、Ki值与其之间的关系。Kp的寻优区间为0～10，步长为2；Ki的寻优区间为0.04～0.1，步长为0.02。目标渠道是一条底坡1/1500，糙率为0.015，边坡为0，总长为26 625 m的渠道。

由于IAQ与IAW指标本质上存在相关关系，文中仅模拟仿真IAQ与IAE与控制器参数之间的关系，得到如下结论：

(1)IAQ与Kp、Ki的关系曲线均呈现类似指数式曲线，当IAQ为最小值时，控制器各参数值集中在0附近，不能很好判别出Kp、Ki较优值的范围。

(2)当Kp值为不同常量时，IAE值随Ki呈现先减小后增大的趋势，类似“U型”曲线。

曲线中间部分变化平稳，当Ki位于0.02～0.04附近，Kp值位于5～8附近时，IAE值在最优区域内。可认为在这段平稳范围内，PID参数的变化对控制器性能改变不大，此时控制器已经达到了比较理想的控制状态。这些范围内的Kp、Ki值可作为较优的PID控制器参数。(3)当Ki为常量时，超调量OVR随Kp值出现先减小后增大的趋势，同时Ki值与衰减率DAM呈现先减少后增大的趋势，类似“V型”曲线。

比较以上几种性能指标，类“U”曲线的IAE和类“V”曲线的OVR与DAM指标宜作为自适应判断指标。

2.4 自适应调节规则

此次仿真采用PI控制器调节，取Kd=0。在常规PID控制中，控制器参数是定值，但在自适应PID控制中，Kp、Ki为关于性能指标值的函数。在进行自适应仿真之前，文中通过对渠段的模拟仿真得到Kp、Ki的函数关系以及IAE、DAM、OVR这三个指标的参考值，制定以下自适应调节规则。

规则1：

(1)IAE最优指标区域为：IAE<0.00015。该区域内，Kp、Ki值均为较优值。

(2)Kp、Ki调节方向判定：IAQ与Kp、Ki的关系曲线均呈现类似指数式曲线，运用IAQ指标判定调节方向。首先，计算PID参数初值对应IAQ指标值， 若IAQ值大于设计流量的2/3，则将参数调小；反之则调大。

(3)调节顺序：根据实验试凑法的原理，Ki值的变化会引起Kp值改变，为保证调节变量的唯一性，先调节Ki再调节Kp。

(4)增加Kp约束：IAE相对变化率小于0.005。

规则2：

(1)最优指标：性能指标DAM、OVR在调节步长内计算出的最小指标。其对应Kp、Ki值即为最优参数。

(2)Kp、Ki调节方向判定：同规则1。

(3)调节顺序：不讲究先后顺序。将OVR最小时对应Kp值、DAM最小时对应Ki值作为控制器参数最优值。

(4)为保证控制器性能，增加关于Ki值的约束：稳态误差ESS<0.01。

3 仿真分析

采用某大型调水工程输水渠道系统总干渠部分渠段作为仿真渠段，使用武汉大学开发的输水渠道系统运行仿真与控制软件V1.0 中的程序包[23]以及作者自行开发的自适应PID控制算法程序进行仿真计算，以探索前述的自适应PID控制算法对渠道的控制效果。

3.1 单渠段自适应PID控制仿真

本节采用单渠段模型进行自适应PID控制模拟仿真，再将控制算法用至该调水工程中多个渠段加以验证。渠段边坡为0，其余模型参数如表1。

表1 某调水工程单渠段参数表

本渠池建模时，每部分渠段之间沿程有渠底降落与渐变段，渠池内设有取水口与调控建筑物，取水口位置接近渠池末端。模型中将渐变段对于渠段间的变化作为水力损失与渠底降落处理，采用下游常水位运行方式，采用工况如下：设置渠道上游初始流量为设计流量32 m3/s，下游初始流量为12 m3/s，取水口分水流量在第3～6 h间由0均匀变为4.5 m3/s，6 h后取水流量保持不变。仿真时间步长为20 min，仿真时间为72 h。

按照2.4节调节规则1，对该调水工程单渠段进行自适应控制模拟仿真：渠系采用下游常水位运行方式，首先设定初值Kp=12，Ki=0.06，然后利用软件[23]进行自适应调节。在本工程中，Ki取值较小，对应IAE的相对变化率较大，因此Ki寻优步长Ki_step取为0.005。而Kp可调范围较大，由程序仿真得到的结果表明，当性能指标值较为理想时，对应控制器参数范围较大，为保证快速找到理想参数，Kp值寻优步长Kp_step取为1。仿真结果如图2、图3。

图2 IAE性能指标自适应调节前后水位误差对比图

图3 IAE性能指标自适应调节前后闸门开度对比

由上图发现，下游闸前水位呈现先减小后增大的过程，这是由于取水口位于下游闸门前，仿真程序未设置蓄量补偿机制，当取水口取水时，上游并未提前补偿蓄量，因此下游闸前水位减小，经过一定滞后时间后，上游闸门水量传递至下游，水位才逐渐抬升。

当Kp=10，Ki=0.02时，渠系控制系统达到理想状态。对比调节前与调节后下游水位误差曲线可以发现：渠道在经过自适应调节后，在12h处水位误差由0.3 m降至0.12 m，随后在原有的基础上逐渐减小，闸门的超调量接近(均为60%)，调节后稳定时间提前15 h。原因是：Kp值经过调节后变化量不大，导致控制器对于闸门调节量有限，但Ki值减小至原先的200%，水位偏差消除较快，闸门能迅速达到稳定状态。经过自适应调节后，稳定时间有所提前，控制器控制效果较好。

根据自适应规则2，对同一渠道进行自适应调节，对比仿真结果。自适应调节步长同规则1：Kp_step=1，Ki_step=0.005。仿真结果如图4、图5所示。

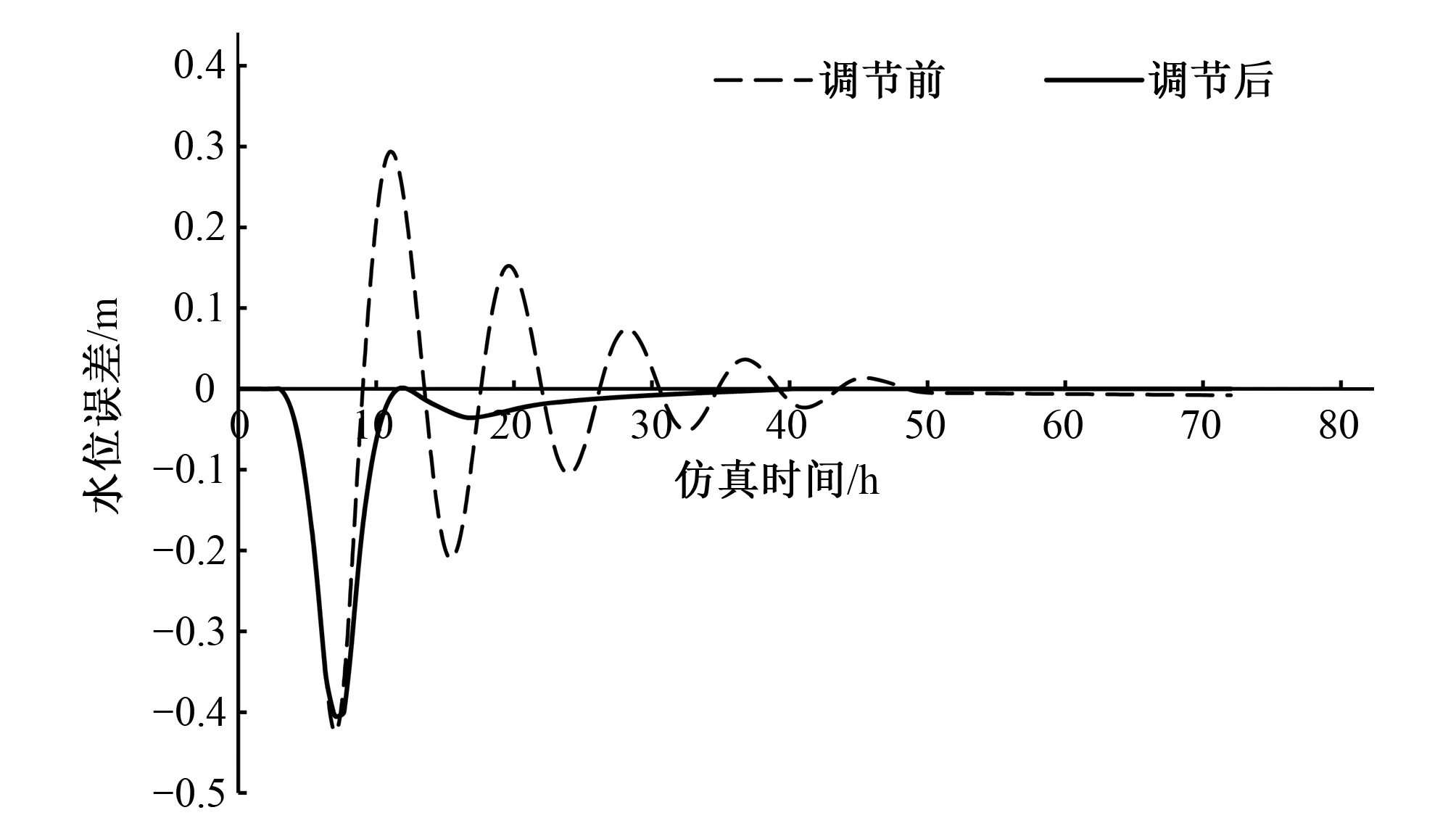
图4 DAM、OVR性能指标自适应调节前后水位误差对比图

图5 DAM、OVR性能指标自适应调节前后闸门开度对比图

经过自适应规则2调节后，得到控制器最优参数Kp=4，Ki=0.02。由图4和图5所示，渠系系统稳定时间在25 h附近，比原先系统提前了20多个小时。超调量在闸门经过一次调节之后不断减小(63%变为40%)，并接近稳定状态，调节后的闸门动作量减少，水位误差曲线经过2次衰减过程即达到稳定，符合自适应规则中关于性能指标的调节要求。

图6 两种自适应调整效果对比图(水位误差)

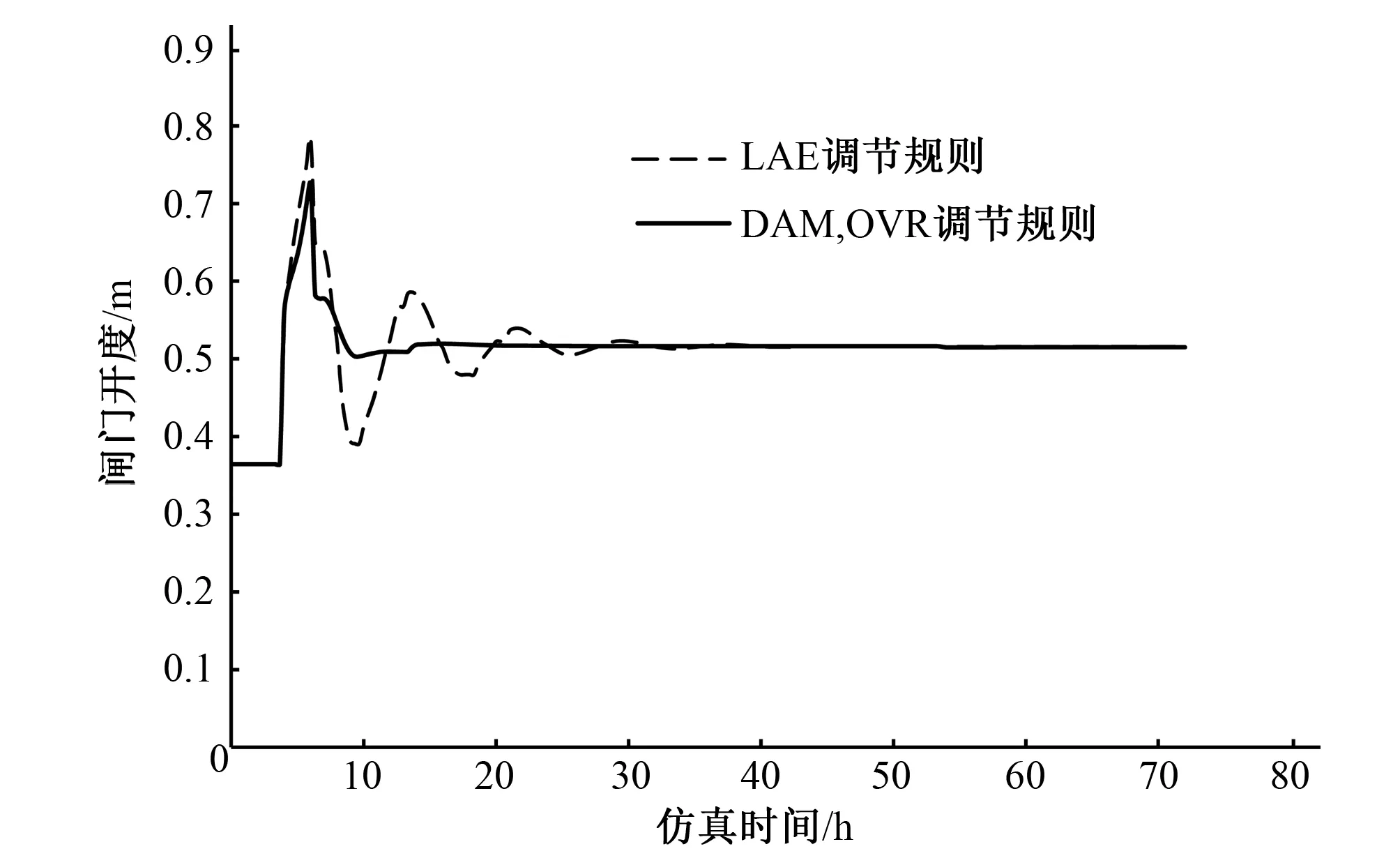
图7 两种自适应调整效果对比图(闸门开度)

对比两种自适应系统调整效果，DAM、OVR调整机制在初始时间下水位误差值与IAE调整机制相差不大，但在渠道的超调量方面前者小于后者，并且后者经过闸门接近10次调节后，系统才趋于稳定，前者仅经过3次调节。DAM、OVR调整机制在仿真进行到25 h时，渠系系统达到稳定状态；而IAE调整机制在接近50 h时才稳定，并且稳态误差相比于DAM、OVR调整机制较大。以上对比结果发现，性能指标最优取值范围与最终调节效果有一定关系。

3.2 多渠段自适应PID控制仿真

多渠段串联系统中，相邻渠段间由节制闸形成耦合关系，闸门调节相邻渠段皆有影响，故多渠段调节性能有异于单渠段。在仿真模型中，为使系统响应更加迅速、调节时间缩短，闸门启闭过程采用同步操作技术。为避免较小的水波扰动对闸门动作的影响，设置闸门死区0.01 m。在渠系控制中，由于多渠段之间的耦合特性，单渠段目标性能指标不再适用。由于单渠段自适应控制仅追求某一特定渠段的性能指标最优化，而对于其他渠段而言，由于耦合作用的影响，其性能指标并不能达到最优，甚至调控效果很差。因此，对整个渠系而言，应采用综合性能指标最优化作为自适应规则，即使所有渠段IAE指标值之和在最优范围。

3.2.1 仿真模型

多渠段自适应控制仿真模型与单渠段自适应模型类似，由于渠系间具有耦合作用，本文做出以下假设：①渠段间Ki值均相同，设为定值。②各渠段中Kp值与断面面积成正比例关系。假设原因如下：

(1)串联渠道间，由于相互耦合作用，Ki值变化量很小。并且渠系系统Ki值调节量不大，且对于闸门开度影响不大，因此取各渠段Ki值相同。

(2)在一定范围内，Kp值变大引起闸门开度的增大，因此过流断面面积增大，Kp值与断面面积间存在类似正比例关系。

在多渠段系统里，首先率定Ki值，取IAE综合指标最优范围对应Ki值作为较优值，然后调整Kp值，Kp的选取以第一渠段为基准，其他渠段的Kp值用断面面积关系进行率定，即：

(7)

式中：Kp1、A1为第一渠段的Kp值与断面面积；Kpn、An后面渠段的Kp值与断面面积；n为渠段号。做此简化主要是与ID模型的机理有关，如此便将多渠段自适应问题转化为单渠段自适应问题，再用上述单渠段自适应规则进行模拟仿真即可。

3.2.2 仿真工况

多渠段模拟仿真计算采用该调水工程3个渠池进行建模，1号渠池边坡为1∶1，2号和3号渠池边坡为0，其余模型参数如表2，建模参数如表2。

表2 某调水工程多渠池参数表

多渠段自适应控制仿真主要采用单渠道自适应控制规则，用于验证单渠段自适应规则的适用性。使用软件[23]进行仿真计算。渠道设计流量为32 m3/s，下游流量为12 m3/s，3个渠池均设有取水口，设计取水流量分别为6 、6.5 m3/s。仿真总时长为72 h，仿真时间步长为20 min，采用下游常水位运行方式，仿真工况如下：

(1)仿真在进行到3 h时，渠池1中取水口开始取水，取水流量从0不断增加，到6 h时流量变为3 m3/s，随后保持不变。

(2)仿真在进行到3 h时，渠池2中取水口开始取水，取水流量从0变成3.5 m3/s，6 h后保持不变。

(3)渠池3取水口未取水

3.2.3 仿真结果

多渠段自适应仿真规则同单渠段自适应规则，并加入3.2.1仿真模型节假设条件，多渠段自适应性能指标为3个渠池IAE指标之和，根据单渠段仿真结果，取IAE之和范围小于0.000 45，即判断控制器经过整定达到理想参数。

对该调水工程整个渠段进行仿真。结果如图8、图9。

图8 调节前各渠段水位误差过程线

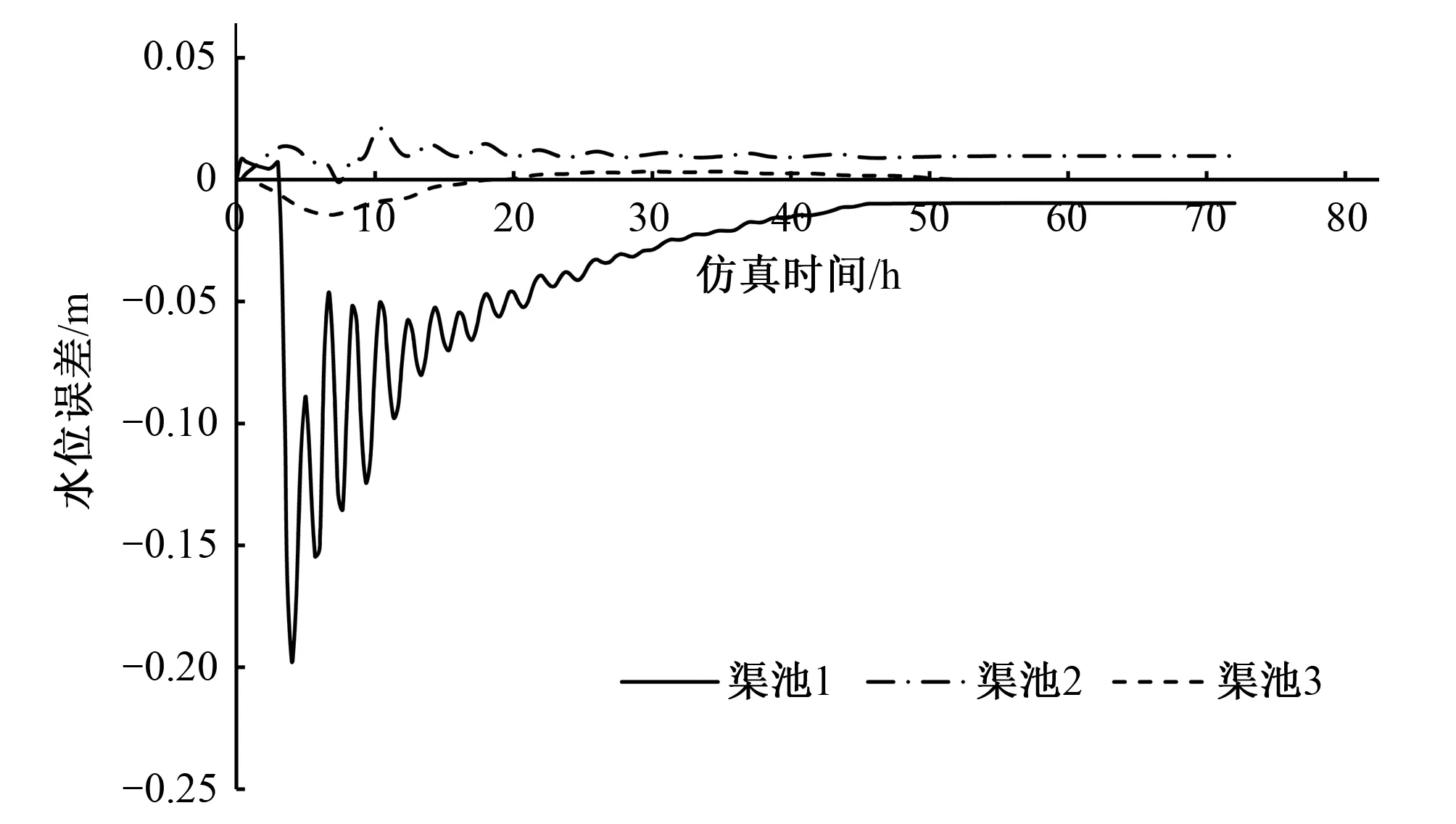
图9 调节后各渠段水位误差过程线

当渠池1中Kp=3，Ki=0.005时，系统性能指标值达到目标性能指标范围。则渠池2参数Kp=2.87、Ki=0.005，渠池3参数Kp=2.88、Ki=0.005。与调节前进行对比，发现3个渠道调节次数减小，稳定时间增加，稳态误差减小。渠池2、3超调量相应减小。达到性能调节要求。

3.3 仿真结果讨论

仿真结果说明自适应PID算法相较于经典PID算法控制性能具有一定的优势，但在实际操作中需要注意自适应规则和调节步长的选取：

(1)对比两种自适应调节规则，IAE规则不具有强约束性，其优化仅能得到较优或可行的控制器参数，DAM、OVR规则则更适宜作为控制器深度优化的参量。IAE规则自适应最优参数很多，易调整，且控制器性能较好。DAM、OVR规则自适应调节效果可达到更好，但调节花费时间较长，若未达到最优指标值，控制器效果可能达不到预期，所以需要根据实际情况合理选择自适应规则。

(2)自适应控制仿真结果与控制器参数调整所取步长有关，若增大调整步长，IAE规则自适应算法也许能得到更优的控制器参数。但增大步长对于整定PID控制器参数而言往往不利，也许会直接跨越最优值。因此控制器参数调整步长值要合理取值。

4 结 语

基于控制领域现有的研究成果，借鉴自适应控制的主要思路，建立了应用于渠道控制系统的自适应控制优化方法，并采用某大型调水工程干渠的部分渠段进行建模并开展仿真分析，比较了几种不同的优化指标的自适应学习效果。仿真结果表明：经过自适应调整，渠系在常规PID算法的基础上系统超调降低、闸门调节量减少，稳定时间增加。说明自适应算法能够有效降低外界因素对于控制器的干扰，使控制器具有实时调整功能，适用于时变性的控制对象，不依赖于精确的数学模型。对于我国广大灌区渠系运行调度以及大型输配水工程的运行管理具有一定的参考价值和应用前景。