点面图的基尔霍夫指标

王大勇,杨玉军

(烟台大学数学与信息科学学院,山东 烟台 264005)

1 引言与预备知识

(1)

后来, 人们进一步将顶点的度考虑进来, 定义了2种修正的基尔霍夫型指标. 一种是度和基尔霍夫指标[2], 记作Kf+(G), 定义为

(2)

其中di表示G中顶点i的度.另一种是度乘积基尔霍夫指标[3], 定义为

(3)

基尔霍夫指标不仅是图上的一个重要的不变量, 而且在化学上还是一个重要的分子结构描述符,在QSAR(定量结构活性关系)和QSPR(定量结构性质关系)中有着重要的应用. 因此, 图的基尔霍夫指标得到了广泛的研究. 基尔霍夫指标的研究主要集中于基尔霍夫指标的计算. 一方面, 对于一些特殊图类, 人们给出了这些图的基尔霍夫指标的精确的显式表达式. 另一方面, 对于一些通过在图上做一元或者二元运算得到的图, 如剖分图、三角化图以及合成图等[4-8], 人们给出了这些图的由原图中的参数表示的基尔霍夫指标计算公式, 从而使得这些图的基尔霍夫指标的计算得到了极大的简化. 在本文中, 我们将给出嵌入在定向曲面上的三角化图G的点面图K(G)的基尔霍夫指标的计算公式. 首先给出点面图的定义.

定义1 设图G是嵌入在定向表面Σ上的三角化图(即每个面都是三角形),顶点集合为V(G)={v1,v2,…,vn},边集合为E(G)={e1,e2,…,em}和面集合为F(G)={φ1,φ2,…,φf}.图G的点面图K(G)定义为

V(K(G))=V(G)∪F(G)

且K(G)的边集合为

V(φ),φ∈F(G)}.

由点面图的定义可以看出, 图G的点面图K(G)可以通过下面的方式得到: 在图G的每个面中插入一个新的顶点, 然后再将新的顶点与所在面的3个顶点连边. 例如, 顶点数为4的完全图K4在平面上的嵌入就是一个三角化图, 该图的点面图K(K4)如图1所示.

图1 完全图K4及其点面图K(K4)Fig.1 The complete graph K4 and its vertex-face graph K(K4)

在本文中, 我们将给出嵌入在可定向曲面上的三角化图G的点面图K(G)的基尔霍夫指标计算公式. 所得结果表明,K(G)的基尔霍夫指标可以由图G的顶点数、面数、顶点的度、基尔霍夫指标等参数表示.

2 点面图的基尔霍夫指标

本节将给出点面图的基尔霍夫指标计算公式. 在给出主要结果之前, 首先介绍电网络中的一个重要结果——Foster公式.

引理1[9]设图G是顶点数为n的连通图,则有

(4)

其中i～j表示顶点i和顶点j相邻,且和号取遍所有相邻的点对.

应用电网络理论中的星形-三角形变换和电阻距离的局部和法则, SHANGGUAN和CHEN得到了点面图的电阻距离计算公式[10],见引理2.

引理2[10]设G是嵌在定向表面Σ的三角化图,顶点集合和面集合分别为V(G)={v1,v2,…，vn}和F(G)={φ1,φ2,…，φf},那么图G点面的K(G)的顶点集合为V(K(G))=V(G)∪F(G)中顶点间的电阻距离为

(1) 如果vi,vj∈V(G),那么

(5)

(2) 如果vi∈V(G),φj∈F(G),V(φj)={a,b,c},那么

(6)

其中rφj(G)=rab(G)+rac(G)+rbc(G);

(3) 如果φi,φj∈F(G),V(φi)={d,e,f},V(φj)={a,b,c},那么

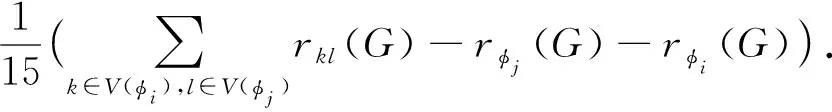
(7)

现在给出本节的主要结果.

定理1 设G是嵌入在定向曲面Σ的顶点数为n且面数为f的三角化图, 则

(8)

证明由基尔霍夫指标的定义以及V(K(G))=V(G)∪F(G), 可知

(9)

下面分别计算等式(9)中等号右边的3项.

(i)首先计算等式(9)等号右边的第一项. 由引理2, 当vi,vj∈V(G)时,

因而,

(10)

(ii)再计算等式(9)等号右边的第二项.由引理2可知,当vi∈V(G),φj∈F(G)(V(φj)={a,b,c})时,

其中rφj(G)=rab(G)+rac(G)+rbc(G).因此

(11)

一方面,∀vj∈V(G),vj同时属于G的dj个不同的面,因此

(12)

(13)

将式(12)和(13)代入式(11), 可得

(14)

(iii) 最后, 计算等式(9)右边的第三项.由引理2, 对φi,φj∈F(G),

rij(K(G))=

因此,

(15)

显然,

rkl(G)中出现了didj-2次, 因此由Foster公式可得

Kf*(G)-2(n-1) .

(16)

另一方面, 同样由Foster公式可得

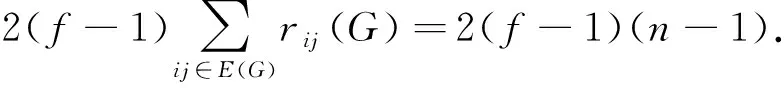
(17)

将等式(16)和(17)代入等式(15), 可得

(18)

综合以上结果, 将等式(10),(14)和(18)代入等式(9), 通过简单运算就可得到定理中的结果.