悬臂式抗滑桩桩间挡板土压力的计算

路 利 民

(河北工程大学土木工程学院，河北 邯郸 056038)

0 引言

抗滑桩具有良好的抗滑效果，被广泛的应用在边坡工程中。根据相邻抗滑桩桩间是否设置挡板，可将悬臂式抗滑桩分为有挡板悬臂式抗滑桩和无挡板悬臂式抗滑桩。对于有挡板悬臂式抗滑桩，当桩间挡板具有一定柔度时，桩后土拱效应可以得到有效的发挥，则作用在桩间挡板上的土压力较经典理论(不考虑桩后土拱效应)得到的土压力值要小[1,2]。因此，在计算桩间挡板土压力值时，需考虑桩后土拱效应，避免资金浪费。

1 土拱效应理论

由于悬臂式抗滑桩自身刚度较周围土体刚度大很多，桩身的水平位移也很小，因此，当桩后土体压力传递至桩身时，抗滑桩会阻止土体位移，并迫使桩后一定范围内的土颗粒之间不断楔紧，形成具有一定强度和厚度的土拱，抗滑桩桩后大部分土体压力通过传递至桩身。简而言之，抗滑桩桩后土拱的形成过程是桩后土体应力重新分布的过程。又因这一过程是自发形成的，则土拱形状必为合理拱轴线，本文假定土拱形状为抛物线形，如图1所示。设抛物线方程为：

y=ax2+b

(1)

则：

y′=2ax

(2)

由Mohr-Coulomb准则可知，若桩后土体处于极限平衡状态，土拱体也处于极限平衡状态。此时土拱体拱脚处所受力最大，大主应力σ1的方向与拱轴线在拱脚处的切线方向一致，与x轴的夹角为θ，θ=45°-φ/2即：

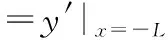
(3)

又因抛物线过(-L，0)，(L，0)，可求得抛物线方程为：

(4)

2 抗滑桩桩间挡板土压力计算

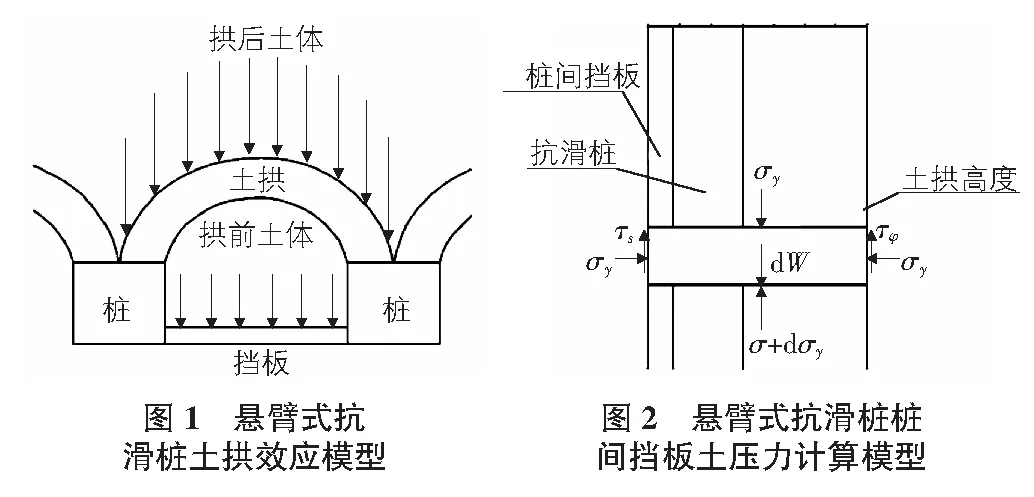
由于抗滑桩桩后存在土拱效应，当桩间土处于极限平衡状态时，可假定土拱拱圈后的滑坡推力由土拱拱圈传递至抗滑桩桩身，而拱圈内的土体则由挡板承担。假定土拱效应沿桩长不发生改变，则可建立如图2所示计算模型。

取图2所示微元体进行分析，对此微元体进行静力平衡分析：

1)微元体重力为：

dW=γAdz

(5)

其中，A为抛物线与桩间挡板间的面积。

2)作用在微元体侧面(即土拱体侧面)的摩擦力为：

Tφ=Sτφdz=Sσztanφdz=KSσytanφdz

(6)

其中，S为抛物线的弧长；K为土体侧向压力系数，可取K=tan2(45°-φ/2)；σz为深度z处土体的竖向压力；σy为作用在桩间挡板上的土压力。

3)作用在挡板与微元体间的摩擦力为：

Tδ=Sτδdz=2Lσztanδdz=2KLσytanδdz

(7)

4)作用在微元体顶部和底部的合力为：

A(σz+dσz)-Aσz=Adσz

(8)

联立式(5)～式(8)，可得：

Sσztanφdz+2Lσztanδdz+Adσz=γAdz

(9)

化简式(9)，可得：

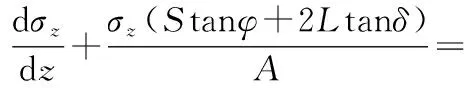
(10)

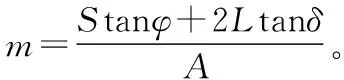
则，式(10)可化简为：

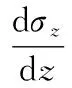
(11)

式(11)通解为：

(12)

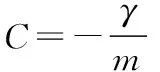
(13)

又因，σy=Kσz，则：

(14)

由式(14)可知，作用在桩间挡板的土压力随深度是一个变化的值，且当深度z趋于无穷大时，桩间挡板土压力为一定值。

3 参数分析

由于施工过程中会遇到各种各样的工况，因此，分析各种工况条件下桩间挡板上的土压力至关重要。