TBM刀盘弹性变形研究
张照煌,洪 文,孙显星
(华北电力大学 能源动力与机械工程学院,北京 102206)
1 研究背景
TBM主要由刀盘系统、驱动系统、支撑系统、推进系统、润滑系统、液压系统、电气控制系统、定位导向系统、衬砌支护系统等多个系统组成[1]。刀盘位于掘进机的最前端,是其关键部件,也是最容易疲劳磨损和引发事故的部件。国内外学者在刀盘的研究方面做出了很多贡献。文献[2]基于弹性力学理论,以刀盘与主轴承间简支、夹支联结关系为边界条件,给出了刀盘在较高作业刚度下刀盘半径和主轴承支撑半径之间的定量关系,并借助ANSYS分析软件验证了该理论;文献[3]将刀盘看成连续性弹性薄板,研究了其变形;文献[4]将刀盘看成非连续性弹性薄板,研究了其变形;孙伟、霍军周等[5-6]基于遗传算法和协同进化思想,在优化滚刀刀间距的基础上提出了平面布置优化设计方法,并对刀盘系统参数及支撑筋等结构进行了优化设计;蔡宗熙、亢一澜等[7]重新推导了刀盘比能的计算模型,对施工实测数据进行了深入分析,给出了在不同工况下盘形滚刀切削深度的最佳范围。刀盘作为盘形滚刀的安装载体,通过驱动系统带动盘形滚刀破碎岩石,承受滚刀破岩传递的全部载荷。由于围岩环境复杂,而且具有高硬度、高耐磨性、成分和构造复杂等特点,刀盘在施工过程中承受着盘形滚刀与岩石相互作用所产生的大推力、大扭矩的强冲击性随机分布载荷,这使得刀盘表现为剧烈的随机振动[8]。刀盘振动是引起刀盘疲劳破坏最主要的原因之一,较大的振动还会引起刀盘主轴承密封失效,刀盘局部损伤等事故,使刀盘的使用寿命大大降低,进而增大施工成本、降低施工效率。因此,研究TBM刀盘在施工载荷作用下的结构力学问题,深入了解刀盘的变形机理及特点,对刀盘结构的设计与加固,以及施工安全隐患问题的预估,都具有重要的意义。
2 刀盘弹性变形理论模型建立
为使掘进机有较好且均衡的破岩效果,掘进机刀盘上盘形滚刀的布置相对比较均匀,整个刀盘由刀盘后的主轴承支撑并传递推进力,见图1所示。通常情况下,可将全断面岩石掘进机刀盘假想为圆形弹性薄板。设刀盘推力引起的岩石反作用力通过盘形滚刀在刀盘上产生的载荷分布集度为q,以刀盘旋转轴线为Z轴,Z轴与刀盘中面的交点为坐标原点,刀盘中面为XY坐标面,根据圆形薄板弯曲理论,刀盘中面在刀盘主轴承和载荷q作用下的弹性曲面微分方程可写为:
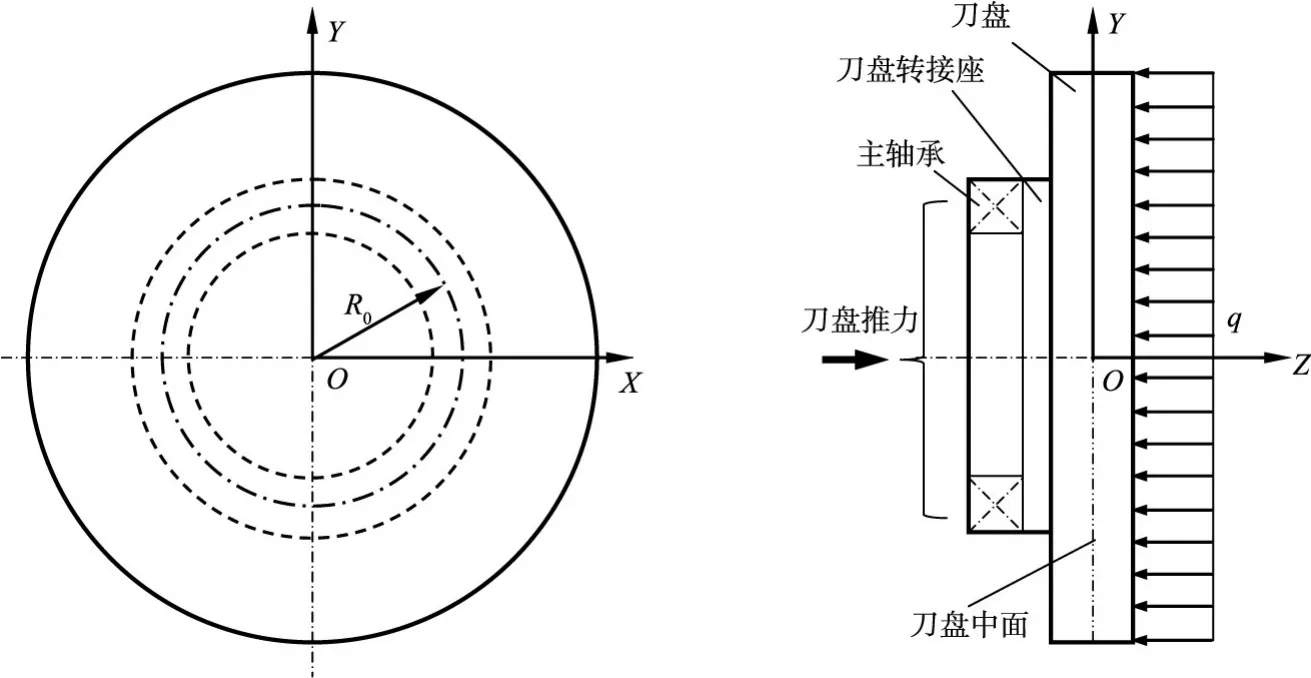
图1 作业刀盘力学模型

式中:D为刀盘弯曲刚度,E为刀盘弹性模量;δ为刀盘厚度;μ为刀盘材料泊松比;r、θ、w为刀盘中面极坐标,其中w与q方向相同取正,方向相反取负。
刀盘上盘形滚刀的布置一般考虑或遵循岩石抗力通过盘形滚刀对刀盘既不产生横向载荷,也不对刀盘产生倾覆力矩的原则。滚刀基本都是绕Z轴对称分布的。亦即w只是r的函数,则公式(1)改写成:

此常微分方程的解为:
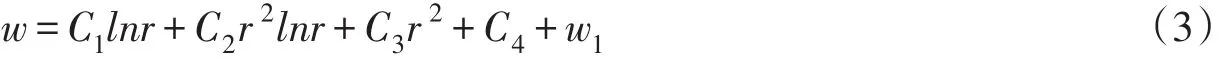
式中:C1、C2、C3、C4为常数,由刀盘结构的边界条件决定;w1为式(2)的任一特解,对受均布载荷q的薄板,有:

由于刀盘中心一般设置中心滚刀,箱形刀盘后面设置刀盘轴承安装座孔,因此C1=C2=0。式(3)改写成:

2.1 简支支撑下刀盘弹性变形设刀盘主轴承支撑半径为R0,当刀盘主轴承与刀盘的联结关系为简支支撑时,有:
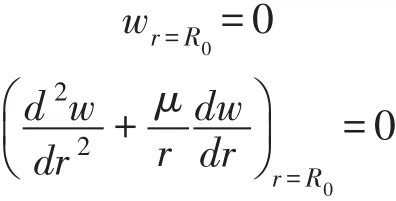
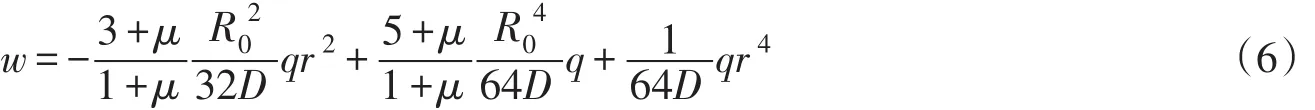
式(6)为刀盘与主轴承为简支联结关系下受均布载荷q作用的中面弯曲弹性变形方程。
2.2 夹支支撑下刀盘弹性变形刀盘轴承支撑半径为R0,当刀盘轴承与刀盘的联结关系为夹支,有:

求解得:
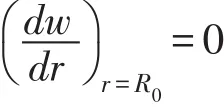
求解得:

式(7)为刀盘与主轴承为夹支联结关系下受均布载荷q作用的中面弯曲弹性变形方程。
3 刀盘变形分析
3.1 外部载荷的确定TBM刀盘上一般安装数十把甚或上百把盘形滚刀,考虑岩石的脆性和岩石质地层的复杂性(如:岩石质的多样性、节理、裂隙及发育程度等),TBM刀盘上每把盘形滚刀的实际受力不仅复杂多变,且具有较强随机性,见图2所示。图2为Z.X.Zhang等[9]在Aspo硬岩实验室进行的掘进机盘形滚刀滚动破岩(正)推力实测时程曲线,其它如盘形滚刀的滚动力实测时程曲线及其侧向力实测时程曲线此处均未引用。通过对时程曲线处理,可得到盘形滚刀滚动破岩正推力、滚动力和侧向力的平均值,从中发现,盘形滚刀滚动力和侧向力约为其正推力的0.1至0.15倍,且盘形滚刀滚动力和侧向力均平行于刀盘中面,因此,刀盘弯曲变形只考虑盘形滚刀正推力的作用;此外,由于每把盘形滚刀正推力大小变化的随机性,便使得数十把甚或上百把盘形滚刀作用在TBM刀盘上的推力具有相对稳定性,为不失一般性,考虑刀盘整体受力为其上所有盘形滚刀滚动破岩正推力平均值的简单累加。

图2 盘形滚刀垂直力时程曲线

式中:q为刀盘正面垂直面载荷;n、m分别为正滚刀与中心滚刀和边滚刀的数量;FNi、FNj为盘形滚刀正推力平均值;S为刀盘面积。
3.2 不同支撑下刀盘弹性变形对比刀盘在垂直面载荷q的作用下,由于主轴承支撑方式的不同,刀盘的弹性变形情况会有所不同。图3给出了在不同载荷作用下刀盘在主轴承简支支撑和夹支支撑时刀盘挠度沿半径的变化趋势。
由图3可以看出,在刀盘主轴承支撑半径R0范围内,简支支撑时刀盘的挠度值大于夹支支撑时刀盘相同位置的挠度值,二者均随刀盘半径的增大而减小,到主轴承支撑半径处减为0。在刀盘主轴承支撑半径到刀盘边缘范围内,随着半径的增大,刀盘挠度逐渐增大,简支支撑下刀盘挠度的增长速率越来越慢,方向与载荷q方向相反;夹支支撑下刀盘挠度的增长速率越来越快,方向与载荷q方向相同。
经上述分析,刀盘所受垂直面载荷集度q为:
4 基于ANSYS的刀盘结构有限元分析

图3 不同载荷、不同支撑条件下刀盘变形沿半径的变化
4.1 建模及初始条件设定刀盘的结构为中方五分式,中心块由前后两层焊接而成,周围四块为整块结构。为了便于ANSYS分析,对刀盘模型做如下简化处理:(1)删除不影响结构强度的螺栓孔特征;(2)删除所有刀具(盘面空洞、开口位置),分析时将载荷施加在整个刀盘正面上;(3)删除结构中的一些斜筋板;(4)圆整三维结构中的尖点,避免出现不必要的尖锐;(5)整体化处理板材焊口与刀盘(二者材料属性相似)。全断面硬岩掘进机刀盘三维模型如图4所示。
4.2 模拟结果与分析刀盘在载荷q的作用过程中,在t=7.35 s时,载荷q达到了最大值283.76 kN/m2,如图5所示。
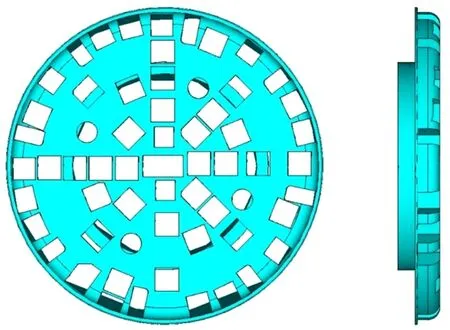
图4 全断面硬岩掘进机刀盘三维模型

图5 qmax=283.76 kN/m2时刀盘弹性变形云图
现将qmax=283.76 kN/m2时刀盘弹性变形有限元模拟结果以极坐标的形式导出刀盘盘面上各节点的坐标与变形量,如表1所示。将刀盘盘面上各节点坐标与变形量以散点图的形式表示,并与相同载荷作用下刀盘支撑方式为简支支撑与夹支支撑时挠度的变化曲线做对比,如图6所示。
刀盘挠度沿半径变化的模拟结果散点图基本介于相同载荷下刀盘支撑方式为简支与夹支时挠度变化曲线之间。由此可见,刀盘主轴承的支撑方式并不是纯粹的简支支撑或夹支支撑,而是介于简支支撑与夹支支撑之间。
为进一步了解TBM刀盘与主轴承之间的联结方式,寻找其中简支支撑与夹支支撑各自所占比重,对刀盘弹性变形有限元计算结果与简支、夹支模型计算结果进行相关性分析,分析方程为:
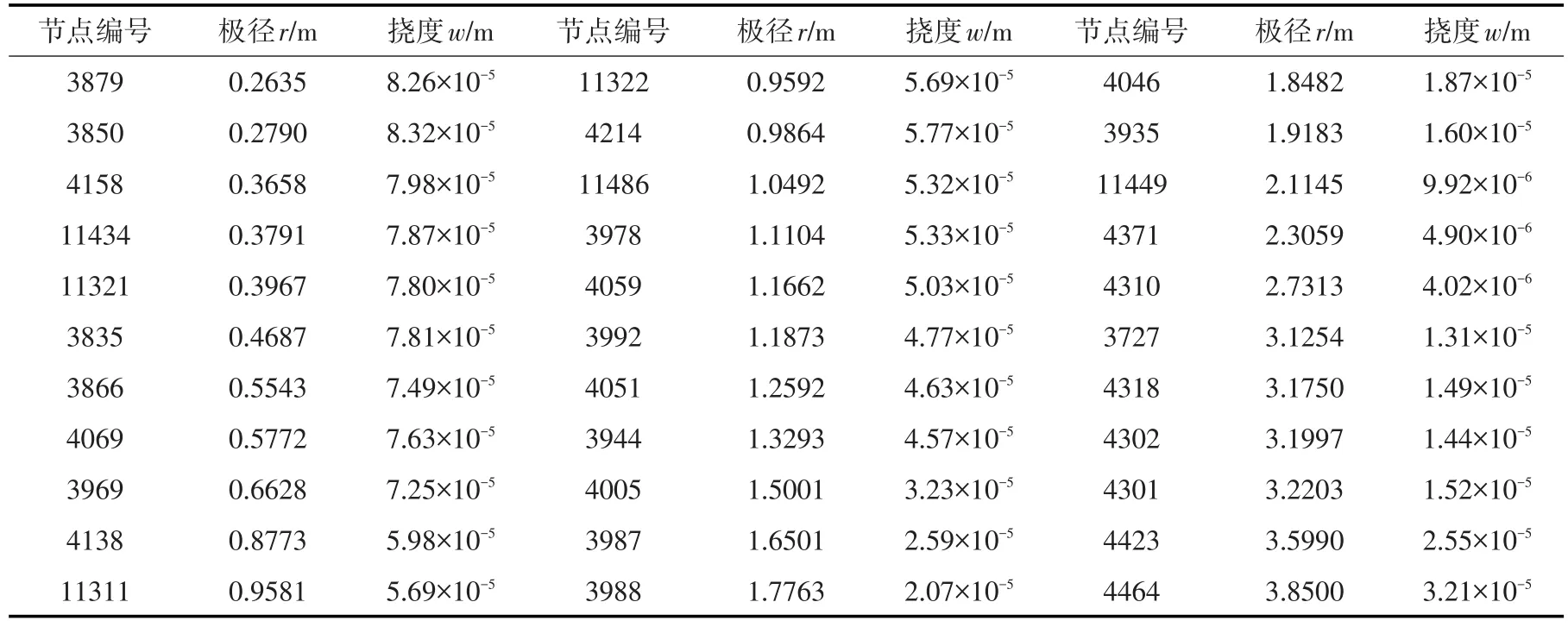
表1 刀盘盘面各节点坐标与变形量(部分)

式中:w0为刀盘弹性变形有限元计算结果;w1为刀盘简支支撑挠弹性变形量;w2为刀盘夹支支撑挠弹性变形量;a、b分别为简支、夹支比重系数,其中a+b=1;ε为随机误差。
根据随机误差计算结果统计可知,当a=0.12~0.16时,随机误差ε均值较小,且变化波动较小,刀盘弹性变形相关性分析结果较为理想,其中以a=0.14最为理想。则在刀盘主轴承支撑半径范围内,刀盘弹性变形与简支、夹支支撑下弹性变形近似线性相关。因此,该型号刀盘弹性变形可由不同支撑方式下中面弯曲微分方程按不同比重关系计算获得,参考下式:
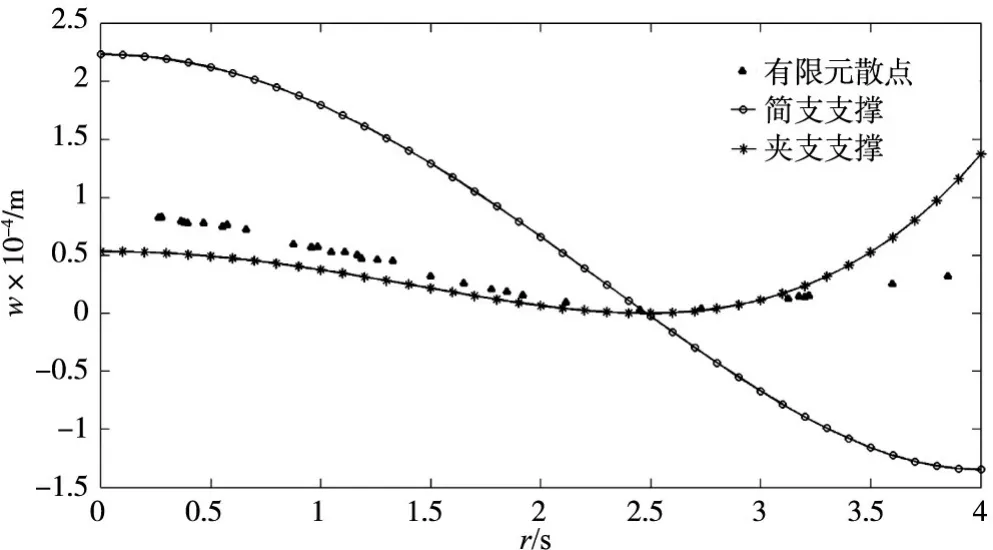
图6 刀盘挠度模拟结果与简支、夹支情况对比

式中:w′为刀盘弹性变形量;w1为刀盘简支支撑弹性变形量;w2为刀盘夹支支撑弹性变形量;a、b分别为简支、夹支比重系数,其中a+b=1,a取0.12~0.16。
另外,经计算分析,在刀盘主轴承支撑半径范围到刀盘边缘之间,由于刮刀槽、遛碴槽,以及边滚刀一定安装倾角等因素影响,刀盘弹性变形与简支、夹支支撑下弹性变形不存在线性相关性,因此不能按照上述计算方法获得刀盘弹性变形情况。
针对上述方法无法计算主轴承支撑半径外刀盘弹性变形,现采用曲线拟合法对刀盘弹性变形散点进行拟合。拟合后的曲线方程为:

该曲线方程的拟合优度为0.994 04,拟合效果比较理想。式(11)亦可作为计算该型号刀盘弹性变形参考公式。拟合曲线如图7所示,曲线方程式中各项系数如表2所示。
5 结论
(1)通过有限元模拟,发现刀盘弹性变形最大处在其中心r=0.28 m的圆域内,且对于指定刀盘,其弹性变形可近似看作半径和载荷的函数;(2)在相同载荷作用下,通过对刀盘弹性变形变化趋势的有限元计算和刀盘简支、夹支支撑理论解的对比分析,得出刀盘实际支撑情况介于简支与夹支之间,其中简支约占12%~16%,夹支约占84%~88%,并给出了刀盘弹性变形的两种计算参考公式。
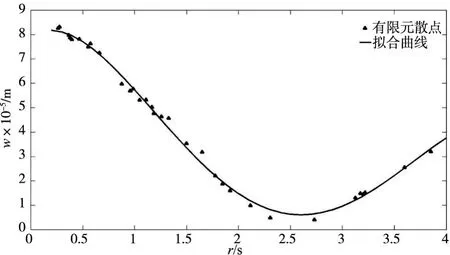
图7 刀盘弹性变形散点图拟合曲线

表2 拟合曲线方程式各项系数值

