飞翼式客机机翼气动/结构综合优化方法研究
宋 倩 万志强 / SONG Qian WAN Zhiqiang
(北京航空航天大学,北京 100191)
0 引言
在现代客机的机翼设计中,需要对气动、结构和内部容积等要求进行综合考虑,以气动和结构的耦合关系为基础,找到一个最佳的设计方案。对于飞翼这种采用新型气动布局的设计方案,相较传统方案,则更需注重考虑气动与结构的耦合关系。
目前,对飞翼布局飞机的单项学科研究较多,研究的重点领域包含气动、隐身、结构、操稳等学科;而对于飞翼布局飞机多学科综合优化研究的相对较少,且在对其进行多学科优化的过程中往往对于气动与结构的耦合问题做出了简化,譬如只将气动载荷单向传递给结构模型,这样获得的结果往往并非准确[1]。针对目前对飞翼客机机翼优化过程中对气动弹性效应考虑不充分、气动/结构耦合不充分的问题,本文开展了针对此类机翼的气动/结构综合优化设计研究,同时获得机翼最优的气动外形和结构构型。
1 理论基础
1.1 静气动弹性响应方程
静气动弹性响应分析方程在f-set的位移向量集下一般可以写为[2]:
(1)

1.2 气动阻力计算方法
气动外形优化设计需要将气动阻力约束考虑在内,但是基于小扰动线化势流理论的面元法无法计算诱导阻力、摩擦阻力以及激波这几类阻力项。若采用基于N-S方程的CFD(Computational Fluid Dynamics,简称CFD)方法虽可以较为精确地得到高精度气动力,但是计算量会剧增,时间耗费巨大,无法满足效率的要求。本文考虑选择基于Euler方程的无黏流方法,结合边界层黏性修正,便可以在满足压力分布、激波阻力、诱导阻力及摩擦阻力的计算要求的同时,有效减少计算时间的耗费。
1.2.1 笛卡尔网格及MGAERO软件
在气动弹性优化中进行气动与结构的耦合分析时,要求结构的变形必须可以准确地反映在CFD网格上。笛卡尔网格是一种特殊的空间离散网格,它网格的生成不依赖于几何外形,免除了贴体网格生成的各种问题。因此,它在需要反复修改网格的气动弹性优化问题中十分适用。
MGAERO是一个以求解欧拉方程为基础的CFD软件。相较其他的CFD软件,MGAERO突出的特点便是采用了多重笛卡尔网格嵌套技术。另外,它所具备的的局部网格加密技术也可以提高效率,减少计算量,加快收敛。MGAERO软件的计算流程如图1所示。

图1 MGAERO软件的计算流程图
1.2.2 黏性修正
在计算摩擦阻力之前需要计算无黏流理论的表面流线,再通过积分该表面流线进行边界层的黏性修正。得到边界层的厚度后,修改原无黏流的边界条件,得到考虑黏性后的压力分布,同时表面流线的改变又会影响边界层厚度,由此即可进行有黏/无黏的迭代修正。
其中,层流边界层计算采用Cohen-Reshotko方法,边界层转捩计算采用Granville方法,湍流边界层计算采用Green方法[3]。
边界层修正是一个迭代的过程,大概需要3~5次黏性/无黏循环,本文的黏性/无黏迭代的流程如图2所示。
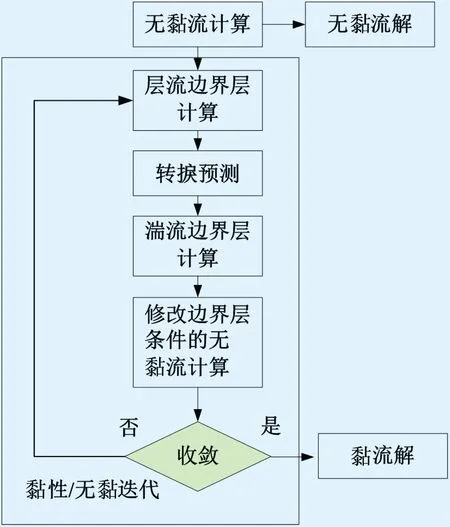
图2 有黏/无黏迭代流程图
1.3 曲面样条插值
在使用MGAERO软件计算机翼巡航阻力前,需要将NASTRAN对模型机翼进行气动弹性分析后得到的位移插值到MGAERO所使用的三维气动模型之上,以求解机翼的巡航阻力。
本文使用曲面样条函数插值方法,其主要思路是:利用已知条件(即已知的独立结点及这些结点所对应的位移)构成一个逼近函数去代替真实函数,从而计算出任何插值点处的位移以及这些插值点处的导数[4]。逼近函数的形式见式(2)。
式(2)中,ε为给定的常数,一般平坦曲面ε=10-2~1,有奇性的曲面取ε=10-5~10-6;c1,c2,L,cN+1+n为待定系数;xpi为第i个结点的第p维坐标。
逼近函数确定后,便可以求出出任一向量Xk对应的函数近似值,此即为插值。
1.4 气动弹性优化
气动弹性优化是一个标准的带约束优化问题,即在n维空间中搜索一组设计变量是目标函数F(v)最小[5]。
MinF(v)=F(x1,x2,K,xn)
ST.gj(v)≤0,j=1,2,K,m
vimin≤vi≤vimax,i=1,2,k,n
其中,v为设计变量,式(3)为目标函数;m为约束的个数,通过式(4)定义约束;为设计变量的个数,式(5)定义了设计变量的上下界。
本文使用遗传算法进行优化,相比敏度算法,遗传算法具备较强的全局搜索能力,能有效避免陷入局部最优解。
1.5 Kriging模型
代理模型可有效解决优化问题中计算耗费大、效率低的问题。响应面方法是一类比较常见的代理模型,其中Kriging模型构建方便,精度高,在实际工程问题中应用较为广泛[6]。
它是一种改进的线性回归方法,由线性回归和非参数两部分构成[6-7]。非参数部分通常采用随机方法,可表示为:
y(x)=F(x)+z(x)
(6)
式(6)中,F(x)是线性回归项,是对全部设计空间的模拟,通过已知的响应进行数据估计;z(x)为非参数随机项,是对全部设计空间的背离,它的协方差矩阵可表示为:
Cov[z(xi),z(xj)]=σ2G(xi,xj)
(7)
式(7)中,G(xi,xj)为任意两点的空间相关方程,可根据需求定义,对模型的精度起决定性作用,应用最广泛的是高斯相关方程。
(8)
式(8)中,θk为相关性参数,ndv为每组采样点中的维数。
相关性参数θk可由极大似然法求得,最终可转化为ndv维的无约束非线性最优问题。求解后便可完全建立一个Kriging模型。
1.6 参数化建模方法
机翼外形最基本的参数是展弦比、根梢比、前缘后掠角、上反角等,这些参数可以唯一确定翼面的形状[8]。机翼的外形参数改变后,虽然所有节点的位置都发生了改变,但机翼的基本结构形式保持不变。所以变参只需改变点的位置即可,在NASTRAN中便体现为对于所有GRID卡片坐标值的修改。变参新建模型的关键在于两点:一是建立初始模型关键点的位置与外形参数的函数关系;二是找到初始模型的所有点和新模型点之间的位置函数关系,并以此关系生成新的GRID卡片。
在整个变参过程中,所涉及到的参数包括两类:外形参数和初始关键点参数。
外形参数有内翼根梢比η1、内翼展弦比λ1、内翼上反角τ1、外翼根梢比η2、外翼展弦比λ2、外翼上反角τ2、后掠角χ,共计七个参数,这七个参数也是对机翼气动弹性性能产生影响的主要参数。
初始关键点参数(与初始模型相关)有翼根前后缘点A1、A2、KINK位置(机翼后缘转折处)前后缘点A3、A4、翼稍前后缘点A5、A6,总计6个点的xyz轴位置参数,如图3所示。
需要指出的是,为计算方便,本文的展弦比中的弦长均为翼根处的弦长。同时,在计算中将内翼展弦比修正为内翼的绝对展长/根部弦长,外翼展弦比同理,外翼根梢比修正为KINK位置弦长/翼稍弦长。

图3 机翼平面投影简化图与参数说明示意图
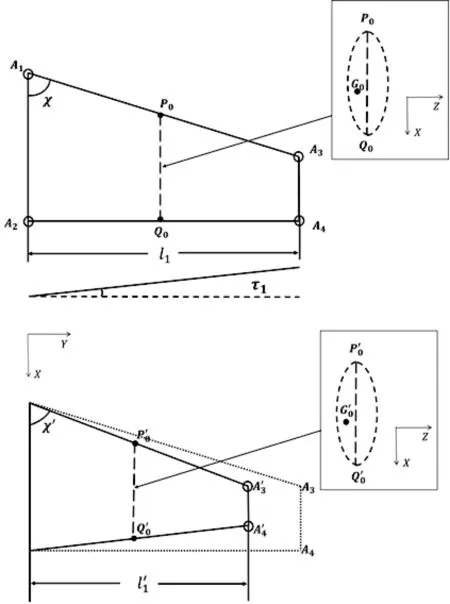
图4 机翼关键点及比例系数计算示意图
如图3所示,机翼可从KINK位置分为内翼和外翼,这两部分可看做两个连接的梯形。就一个梯形区域而言,如图4所示,对机翼进行变参计算的流程如图5所示。其中,各比例系数计算式见式(9)~式(11)。
k1=(yG0-yA1)/l1
(9)
k2=(xG0-xP0)/(xQ0-xP0)
(10)
K3=(zG0-zP0)/(xQ0-xP0)
(11)
其中,k1为展向比例系数,k2为弦向比例系数,k3为厚度方向比例系数。

图5 变参计算流程图
2 机翼气动/结构综合优化框架
2.1 常规优化流程
本文的综合优化设计方法考虑了各个子学科间的耦合作用,同时得到最佳气动外形、结构布局以及结构参数分布,避免反复设计,从而为机翼设计提供参考。在满足精度及效率的前提下,气动子学科选用亚声速偶极子格网法以及基于Euler方程的CFD方法;结构子学科选用有限元分析方法,优化算法采用遗传算法。
整体优化流程如图6所示。

图6 常规综合优化流程图
常规优化流程中由于需要对每一个个体进行CFD气动阻力计算,时间耗费巨大,故引入Kriging代理模型进行机翼气动/结构综合优化。此常规优化流程则可将气动阻力约束去掉进行优化(即不执行图3中红色虚线框内的操作),可将此结果作为后者结果的对比。
2.2 基于Kriging模型的优化流程
基于代理模型的优化流程包括代理模型的建立和遗传优化两个部分,如图7所示。
具体步骤如下:
1)准备初始模型(NASTRAN:机翼三维板杆模型和平板气动模型;MGAERO:三维气动模型)。
2)准备输入文件,输入文件包括控制文件和模型文件。
3)通过拉丁超立方抽样在设计变量空间内选取2 000个样本点。
4)根据平板气动模型和结构模型进行气动弹性分析,将气动弹性分析得到的变形插值到CFD模型上,对插值处理后模型的巡航外形进行流场分析。
5)对样本中的每一个个体执行步骤4)~5)的操作,得到样本的响应值。
6)构建代理模型。
构建完毕后,便可进入到遗传优化中进行计算,在满足精度要求的前提之下,代理模型则类似于一个“黑匣子”,在输入不同的个体后,便可以近似地计算出各个个体的响应,极大地提高优化设计效率。
在优化满足结束条件,输出最优个体后,再对该个体进行真实响应值的计算,若不满足约束要求,则更新个体,重新生成初代群体,重新开始优化;若满足约束要求,则优化结束。
3 算例模型
3.1 三维有限元模型
本文研究所用的飞机机翼半翼展约29 m,采用双梁式结构。机翼上下蒙皮、前后梁腹板采用板单元;前后梁凸缘、上下桁条采用杆单元。材料为铝合金,弹性模量72 GPa,剪切模量27 GPa。有限元模型及机翼内部结构如图8~图9所示。
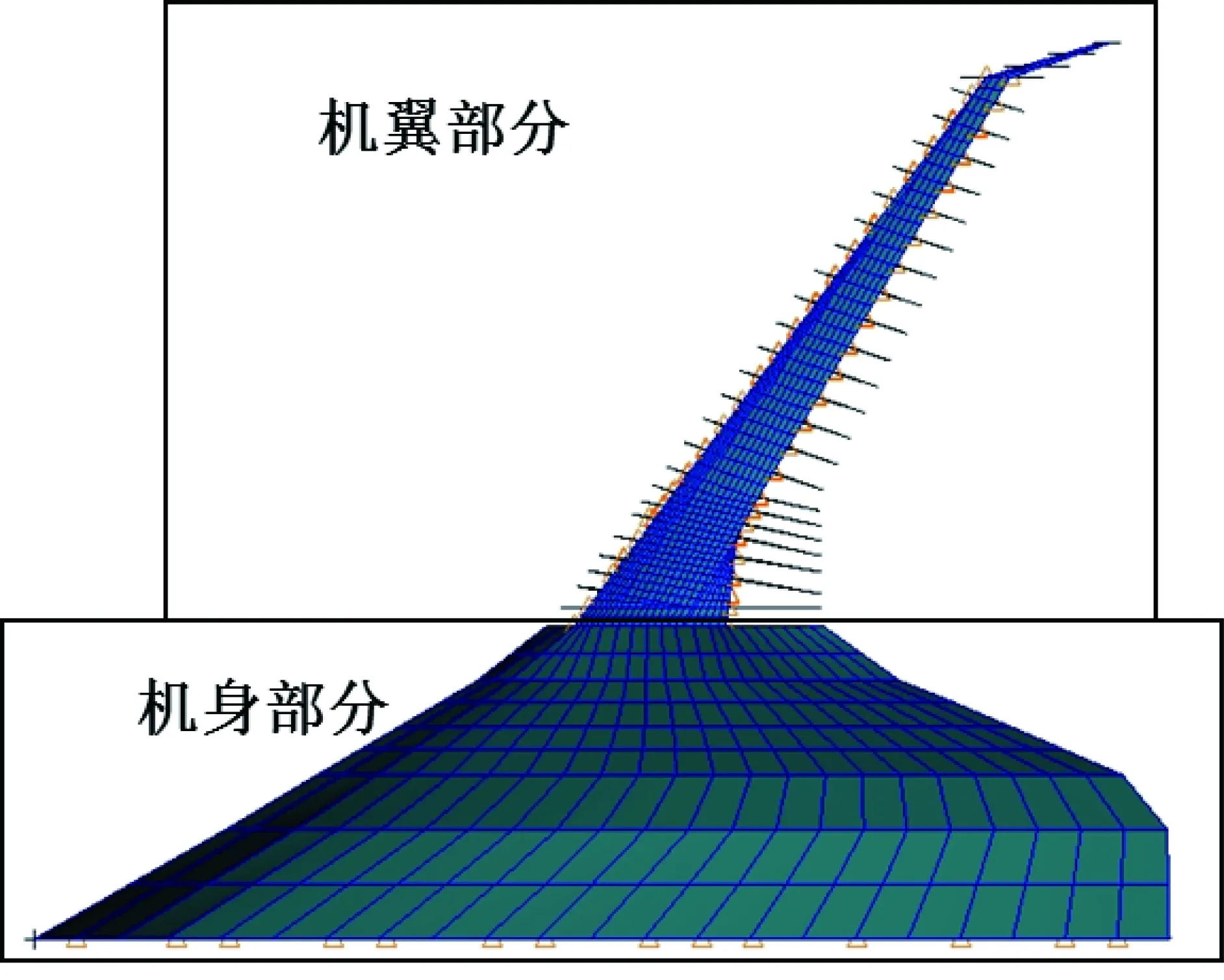
图8 有限元模型

图9 机翼内部结构示意图
模型机身部分采用很硬的壳单元,未建立内部结构。机翼部分为模型的主要部分,建模则较为细致。
3.2 平板气动模型
本文将模型的右半部分机翼及机身划分成为具有不同网格密度的7块平板升力面,如图10所示。

图10 平板气动模型
3.3 CFD三维气动模型
本文在MGAERO中建立的三维气动模型及其空间网格如图11所示。

图11 三维气动模型
4 优化问题描述
本文对飞翼布局大型客机机翼的气动/结构综合优化共包含201个设计变量,其中包括7个机翼外形参数和194个结构参数(上下蒙皮厚度及前后梁上下凸缘面积)。
优化以结构质量最小为目标函数,约束条件包括:翼尖位移、翼尖扭角、颤振速度及气动阻力。
本文对飞翼布局大型客机机翼气动/结构进行综合优化给定的巡航条件为11 000m的飞行高度,马赫数为0.8,配平重量为185t。
5 代理模型的构建及精度校验

图12 目标函数相对误差

图13 翼尖扭角相对误差

图14 翼尖位移相对误差

图15 气动阻力相对误差
本文使用2 000个样本用于模型构建,另外50个样本用于精度校验,各响应的相对误差如图12~图15所示。目标函数的平均相对误差为0.43%,翼尖位移的平均相对误差为4.71%,翼尖扭角的平均相对误差为3.73%,气动阻力的平均相对误差为4.86%,颤振的相对误差由于其特殊性恒为0%,满足优化设计的需求。
6 计算结果
本文对不考虑气动阻力约束的常规优化(以下简称常规优化)以及基于代理模型考虑气动阻力约束的优化(以下简称代理优化),二者优化的结果见表1。

表1 优化结果
代理优化结束条件设定为达到指定的最大迭代代数,本文共迭代200代,每代个体数为1 000。代理优化每代最优个体的目标函数响应及每代个体的适应度情况如图16、图17所示。

图16 目标函数响应随迭代次数的变化趋势

图17 每代最优个体适应度和平均适应度变化趋势
采用这两类方法对机翼进行综合优化设计后的机翼外形参数见表2。

表2 外形参数对比
使用代理模型进行气动/阻力综合优化总耗时为3 360 s,不到一个小时,可以在满足精度的前提下,极大地提高计算效率。
从设计结果的响应值可以看出,不考虑气动阻力约束的常规优化虽有效地减小了目标函数,但气动阻力系数却有所增加,不满足设计要求,如此便造成了反复设计。在引入了Kriging代理模型进行气动/结构综合优化,将气动阻力约束考虑在后,可在精度允许范围内,显著减少机翼的结构质量以及气动阻力。
可以看出,常规优化后的机翼外形整体变小,这也是机翼整体减重的重要原因之一;而代理优化后的外形变化最为明显的则是机翼外翼部分变长、后掠角增大。
初始机翼及在两类优化方法下,最优个体的上下翼面压强分布对比如表3所示。从表中各图可以看出,由于机翼外形的变化,机翼表面靠近前缘部分的压力分布变化较大,而其他区域变化较小。代理优化后,飞机上下表面的压力变化更为光顺,阶跃突变减少,这有利于在保证一定升力的同时,减小气动阻力。

表3 各模型上下翼面Cp分布对比
在0.8马赫数的巡航条件下,大型客机机翼上表面会出现局部激波,相比于黏性阻力,激波阻力和诱导阻力是飞行阻力中非常重要的。前缘后掠角的增加可有效减少上翼面的超声速区域,从而降低局部激波阻力。表4给出了三个阶段设计结果机翼与初始模型上翼面马赫数的对比,可以看出,与初始模型及常规优化结果比较,考虑阻力约束的代理优化结果其超声速区域可大大降低。

表4 各模型上下翼面Ma分布对比
7 结论
对于飞翼这种采用新型气动布局的设计方案,相较于传统方案,更需注重考虑气动与结构的耦合关系。由本文对飞翼布局客机机翼气动/结构综合优化所得结果的分析和对比中可以看出:一方面,将阻力约束考虑在内的气动/结构综合优化,可以在减重的同时,显著地减少气动阻力,同时获得机翼的最优气动外形和结构布局;另一方面,基于代理模型的气动/结构综合优化极大地减少了时间的耗费,且其结果的精度满足要求,具备有较好的工程适用性。

