三角直觉逼近在模糊系统可靠性上的应用

李舒阳, 李洪兴, 孙凯彪

(1. 海军大连舰艇学院 基础部, 辽宁 大连 116018; 2. 大连理工大学 控制科学与工程学院, 辽宁 大连 116024)

0 引言

随着高科技产业的快速发展,工程系统越来越大型化和复杂化,系统可靠性分析已经成为工程领域的研究热点与难点之一.故障树分析方法是系统可靠性分析方法中一种应用最为广泛的分析方法.很多系统存在大量的模糊不确定性,要得到基本事件的确切概率是困难的.因此，Tanaka等[1]将模糊理论引入故障树分析,用模糊概率代替传统可靠性分析中的精确概率值.文献[2]用三角形直觉模糊数表示系统部件失效概率,提出一种直觉模糊故障树分析算法计算系统部件的故障区间,为管理人员找到最关键的系统部件提供决策参考,并将此算法应用到印刷电路板装配中.文献[3]提出一种直觉模糊故障树分析方法解决液化天然气终端紧急关闭系统的故障分析问题.文献[4]通过L-R型三角直觉模糊集表示的直觉模糊故障树分析计算机安全系统的可靠性.文献[5]利用故障树分析部件用梯形直觉模糊数表示的船舶动力装置的可靠性.文献[6]修改文献[1]模糊故障树的定义,应用故障树分析、三角直觉模糊数的α-截集和建立在三角直觉模糊数代数运算上的弱t-范数,得到了系统的故障区间和可靠区间.

在模糊系统可靠性分析中,很多成果都是假设一个系统所有部件的故障率是相同类型的直觉模糊数,然而,这种情况很少发生.在实际问题中,系统部件的可靠性往往用不同类型的直觉模糊数描述.文献[7]给出一种算法，分析了部件用不同类型的直觉模糊数表示的系统的模糊可靠性.通过非线性规划方法计算直觉模糊函数解决模糊系统可靠性问题,数值例子用的是三角和梯形直觉模糊数.文献[8]给出基于α-和β-截集的直觉模糊数的代数运算,由此得到一种系统部件的可靠性用不同类型直觉模糊数表示的模糊系统可靠性分析的方法.该文献里的数值例子中用的也是三角和梯形直觉模糊数.文献[9]针对用不同类型直觉模糊数表示部件直觉模糊故障率的系统,提出构建串并联系统模糊可靠性隶属函数和非隶属函数的算法,这种算法是通过非线性规划方法用直觉模糊函数实现的.数值例子用的是三角形和梯形直觉模糊数说明评估过程和方法,从而减少计算量.文献[10]用弱t-范数的方法对用不同类型的直觉模糊数表示所有部件故障率的系统进行了可靠性分析;但是这种方法需要对直觉模糊数的截集进行代数运算,计算量较大.文献[11]考虑部件的故障率是用三角和梯形直觉模糊数表示的,使用可信性理论计算直觉模糊函数,提出一种分析串联和并联系统模糊可靠性的方法.

虽然关于模糊系统可靠性的研究成果很多,但是仍然有各自的不足之处.如果能有一种评估模糊系统可靠性的方法,不仅评估过程相对简单,计算量小,而且能解决系统部件用不同类型的直觉模糊数(包括一般直觉模糊数)表示的可靠性评估问题,将对模糊系统可靠性的发展有着深远的意义.本文提出一种解决实际问题中遇到的系统部件故障率用不同类型直觉模糊数表示模糊系统的可靠性问题的方法,并用直觉模糊数的代数运算分析模糊系统的可靠性,比已有方法的计算量小.最后通过印刷电路板组件(PCBA)故障分析表明,应用本文所给出的梯形直觉逼近方法处理数据后,所得的结果与其它的计算结果相比缩小了直觉模糊数截集的区间长度,提高了结果的可信度.

1 预备知识

1.1形直觉逼近

定义1[12-13]设X是一个给定的非空集合,A={〈x,μA(x),νA(x)〉:x∈X},μA:X→[0,1],νA:X→[0,1],且对∀x∈X有0≤μA(x)+νA(x)≤1,称A为X上的直觉模糊集.

如果直觉模糊集A满足一定的条件,那么称A为正规直觉模糊集.

定义2[14]设A={〈x,μA(x),νA(x)〉:x∈X}是论域X上的直觉模糊集，如果至少存在2点x1,x2∈X，使得μA(x1)=1,νA(x2)=1，则称直觉模糊集A是正规的.

直觉模糊集的一种特殊情形称为直觉模糊数.

定义3[14]设A={〈x,μA(x),νA(x)〉:x∈R}是实轴R上的一个直觉模糊子集,如果下面条件成立:

1)μA(x)是模糊凸的，即对∀x1,x2∈R,λ∈[0,1],有

μA(λx1+(1-λ)x2)≥

min{μA(x1),μA(x2)},

νA(x)是模糊凹的，即对∀x1,x2∈R,λ∈[0,1],有

νA(λx1+(1-λ)x2)≤max{νA(x1),νA(x2)};

2)A是正规的;

3)μA是上半连续的,νA是下半连续的;

4) SupA={x∈R:μA(x)>0,νA(x)<1}是有界的.

则称A为一个直觉模糊数.

如果μA和1-νA是梯形模糊数,那么称直觉模糊数A=〈μA,νA〉是梯形直觉模糊数;如果μA和1-νA是三角形模糊数,那么称直觉模糊数A=〈μA,νA〉是三角形直觉模糊数.如果A=〈μA,νA〉是一个直觉模糊数,T△(A)=〈μT△,νT△〉是距离A=〈μA,νA〉最近的那个三角形直觉模糊数,称T△(A)=〈μT△,νT△〉为A=〈μA,νA〉的三角直觉逼近.

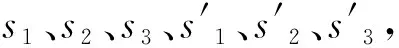
(μA)U(α))dα,

(1)

(2)

(3)

(1-νA)U(α))dα,

(4)

(5)

(6)

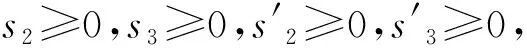
(μT△)α=[s1-(1-α)s2,s1+(1-α)s3],

⋮

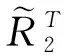
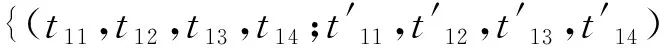
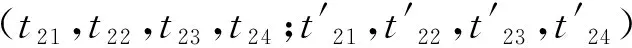
(7)

图1串联系统
Fig.1Seriessystem

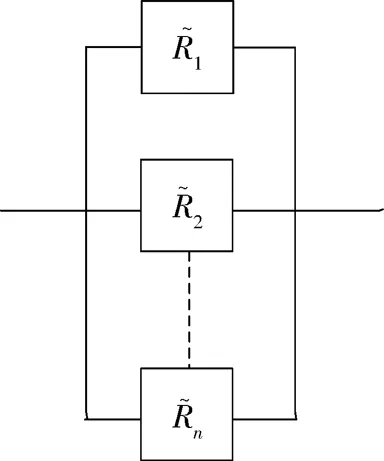
图 2 并联系统Fig.2 Parallel system

⋮

(8)

2 算例分析

给出一个印刷电路板组件(PCBA)的例子说明所提出来的逼近方法分析系统模糊可靠性的过程,并与文献[17-18]的方法比较.图3的PCBA故障树和数据来自台湾新竹科学园区一个中型制造厂[2].这里使用PCBA作为故障树的顶部事件.印刷电路板组件故障的故障树如图3所示,子事件和底部事件详见表1和表2.

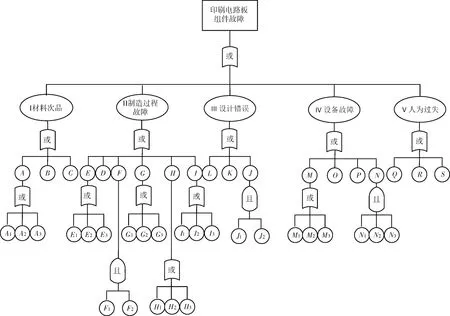
图 3 印刷电路板组件故障树的图像Fig.3 The fault-tree diagram of PCBA fault

由于基本事件的故障率数据不完全,故障率密度函数类型不同等原因,根据专家的观点给出了故障树底部事件的故障率,故障率用以下的不同类型的直觉模糊数表示.

A1=〈μA1,νA1〉是三角形直觉模糊数,有

(μA1)α=

[0.000 7+0.000 4α,0.001 24-0.000 14α],

(1-νA1)α=

[0.000 58+0.000 52α,0.001 51-0.000 41α].

A2=〈μA2,νA2〉是三角形直觉模糊数,

(μA2)α=

[0.000 96+0.000 14α,0.001 34-0.000 24α],

(1-νA2)α=

[0.000 72+0.000 38α,0.001 49-0.000 39α].

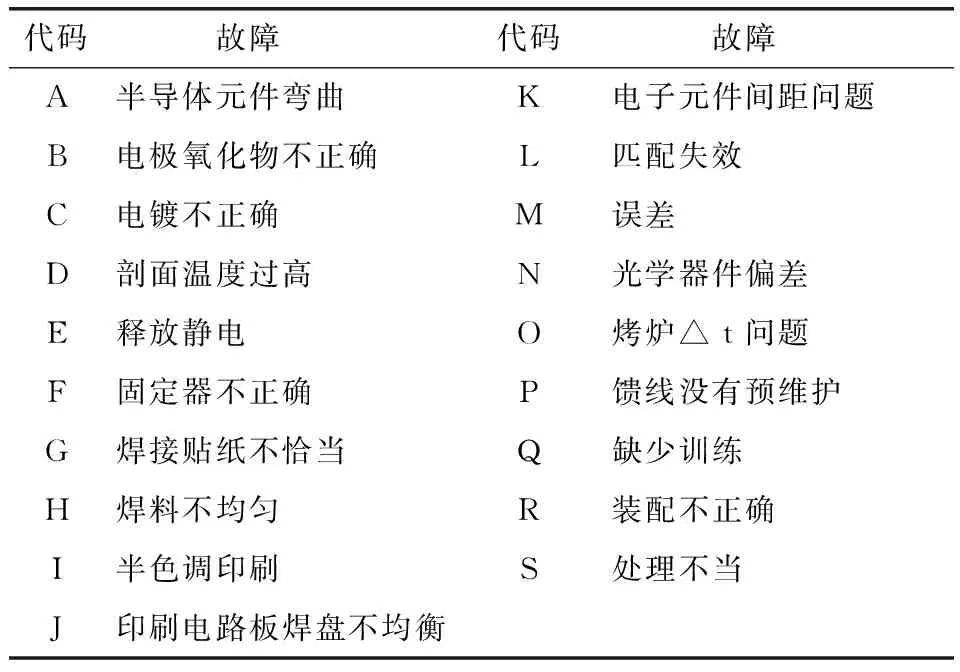
表 1 PCBA故障子事件的说明Tab.1 The descriptions of the sub-events of PCBA fault

表 2 PCBA故障底部事件的说明Tab.2 The descriptions of the bottom events of PCBA fault

A3=〈μA3,νA3〉是三角形直觉模糊数,

(μA3)α=[0.004 11+0.000 62α,0.005 13-0.000 4α],

(1-νA3)α=[0.002 89+0.001 84α,0.005 57-0.000 84α].

B=〈μB,νB〉是梯形直觉模糊数,

(μB)α=

[0.001 11+0.000 09α,0.001 78-0.000 08α],

(1-νB)α=

[0.000 89+0.000 31α,0.001 92-0.000 22α].

C=〈μC,νC〉是正态型直觉模糊数,

(μC)α=(1-νC)α=[0.000 99-

D=〈μD,νD〉是尖γ型直觉模糊数,

(μD)α=

(1-νD)α=

E1=〈μE1,νE1〉是正态型直觉模糊数,

(μE1)α=(1-νE1)α=

E2=〈μE2,νE2〉是正态型直觉模糊数,

(μE2)α=(1-νE2)α=[0.000 77-

E3=〈μE3,νE3〉是尖γ型直觉模糊数,

(μE3)α=

(1-νE3)α=

F1=〈μF1,νF1〉是三角形直觉模糊数,

(μF1)α=

[0.001+0.000 1α,0.001 62-0.000 52α],

(1-νF1)α=[0.000 683+0.000 417α,

0.001 82-0.000 72α].

F2=〈μF2,νF2〉是三角形直觉模糊数,

(μF2)α=[0.001 85+0.000 35α,

0.002 59-0.000 39α],

(1-νF2)α=[0.001 49+0.000 71α,

0.002 99-0.000 79α].

G1=〈μG1,νG1〉是梯形直觉模糊数,

(μG1)α=[0.000 496+0.000 024α,

0.000 79-0.000 09α],

(1-νG1)α=[0.000 273+0.000 247α,

0.000 86-0.000 7α].

G2=〈μG2,νG2〉是梯形直觉模糊数,

(μG2)α=[0.002 54+0.000 46α,

0.003 95-0.000 55α],

(1-νG2)α=[0.000 233+0.002 763α,

0.004 61-0.001 21α].

G3=〈μG3,νG3〉是梯形直觉模糊数,

(μG3)α=[0.000 96+0.000 04α,

0.001 71-0.000 11α],

(1-νG3)α=[0.000 517+0.000 483α,

0.002 07-0.000 47α].

H1=〈μH1,νH1〉是尖γ型直觉模糊数,

H2=〈μH2,νH2〉是正态型直觉模糊数,

(μH2)α=(1-νH2)α=[0.002 97-

H3=〈μH3,νH3〉是尖γ型直觉模糊数,

(μH3)α=

(1-νH3)α=

I1=〈μI1,νI1〉是正态型直觉模糊数,

(μI1)α=(1-νI1)α=[0.003 3-

I2=〈μI2,νI2〉是正态型直觉模糊数,

(μI2)α=(1-νI2)α=[0.003 3-

I3=〈μI3,νI3〉是正态型直觉模糊数,

(μI3)α=(1-νI3)α=[0.002 42-

J1=〈μJ1,νJ1〉是三角形直觉模糊数,

(μJ1)α=[0.004 41+0.000 21α,

0.004 95-0.000 33α],

(1-νJ1)α=[0.001 88+0.002 74α,

0.005 51-0.000 89α].

J2=〈μJ2,νJ2〉是三角形直觉模糊数,

(μJ2)α=[0.001 94+0.000 7α,

0.002 85-0.000 21α],

(1-νJ2)α=[0.001 88+0.000 76α,

0.002 91-0.000 27α].

K=〈μK,νK〉是尖γ型直觉模糊数,

(μK)α=

L=〈μL,νL〉是三角形直觉模糊数,

(μL)α=[0.001 06+0.000 15α,

0.001 68-0.000 47α],

(1-νL)α=[0.000 83+0.000 38α,

0.002 05-0.000 84α].

M1=〈μM1,νM1〉是三角形直觉模糊数,

(μM1)α=[0.004 61+0.001 22α,

0.005 92-0.000 09α],

(1-νM1)α=[0.002 59+0.003 24α,

0.006 17-0.000 34α].

M2=〈μM2,νM2〉是三角形直觉模糊数,

(μM2)α=[0.000 203+0.000 017α,

0.000 28-0.000 06α],

(1-νM2)α=[0.000 184+0.000 36α,

0.000 45-0.000 23α].

M3=〈μM3,νM3〉是三角形直觉模糊数,

(μM3)α=[0.001 19+0.000 24α,

0.001 61-0.000 18α],

(1-νM3)α=[0.001 02+0.000 41α,

0.001 93-0.000 5α].

N1=〈μN1,νN1〉是三角形直觉模糊数,

(μN1)α=[0.001 97+0.000 34α,

0.002 58-0.000 27α],

(1-νN1)α=[0.001 91+0.000 4α,

0.002 73-0.000 42α].

N2=〈μN2,νN2〉是三角形直觉模糊数,

(μN2)α=[0.001 04+0.000 28α,

0.001 39-0.000 07α],

(1-νN2)α=[0.000 862+0.000 458α,

0.001 42-0.000 1α].

N3=〈μN3,νN3〉是三角形直觉模糊数,

(μJ1)α=[0.001 45+0.000 31α,

0.001 88-0.000 12α],

(1-νJ1)α=[0.001 17+0.000 59α,

0.002 51-0.000 45α].

O=〈μO,νO〉是尖γ型直觉模糊数,

(μO)α=

(1-νO)α=

P=〈μP,νP〉是梯形直觉模糊数,

(μP)α=

[0.002 58+0.000 12α,0.003 06-0.000 12α],

(1-νP)α=[0.002 11+0.000 59α,

0.003 27-0.000 33α].

Q=〈μQ,νQ〉是正态型直觉模糊数,

(μQ)α=(1-νQ)α=

R=〈μR,νR〉是尖γ型直觉模糊数,

(μR)α=

(1-νR)α=

S=〈μS,νS〉是正态型直觉模糊数,

(μS)α=(1-νS)α=[0.004 18-

下面用不同的方法对PCBA故障模型进行可靠性评估,并对结果进行对比分析.对系统基本事件故障率数据不完整的情况,文献[17]提出了直觉模糊故障树分析的方法.根据专家的知识和经验对底部事件的故障率用三角形直觉模糊数进行代数运算,计算顶部事件PCBA故障的可能性是:

q=〈0.040 794,0.055 720,0.069 499;

0.032 797,0.055 720,0.075 212〉.

当α=0,0.1,0.2,…,1时,根据直觉模糊数的α-截集计算出顶部事件CBA故障的信任隶属区间和非隶属区间,如表3所示.这种方法只能对用三角形直觉模糊数表示的故障率进行运算,有很大的局限性.

表 3 PCBA故障在不同截集水平的模糊故障率[17]Tab.3 Fuzzy failure probability of PCBA fault at different level[17]

文献[18]根据直觉模糊集的区间代数运算评估模糊系统的可靠性,需要先计算35个底部事件,当α=0,0.1,0.2,…,1时的770个α-截集;然后当α=0,0.1,0.2,…,1时,对这些截集再进行区间代数运算,得出顶部事件PCBA故障的信任隶属区间和非隶属区间在α=0,0.1,0.2,…,1时的情况,如表4所示,这种方法计算量比较大.

表 4 PCBA故障在不同截集水平的模糊故障率[18]Tab.4 Fuzzy failure probability of PCBA fault at different level[18]

下面考虑本文提出的逼近方法.从图4可以看到,三角形直觉模糊数比梯形直觉模糊数更接近正态型和尖γ型直觉模糊数.

(a)C的隶属函数和非隶属函数的图像

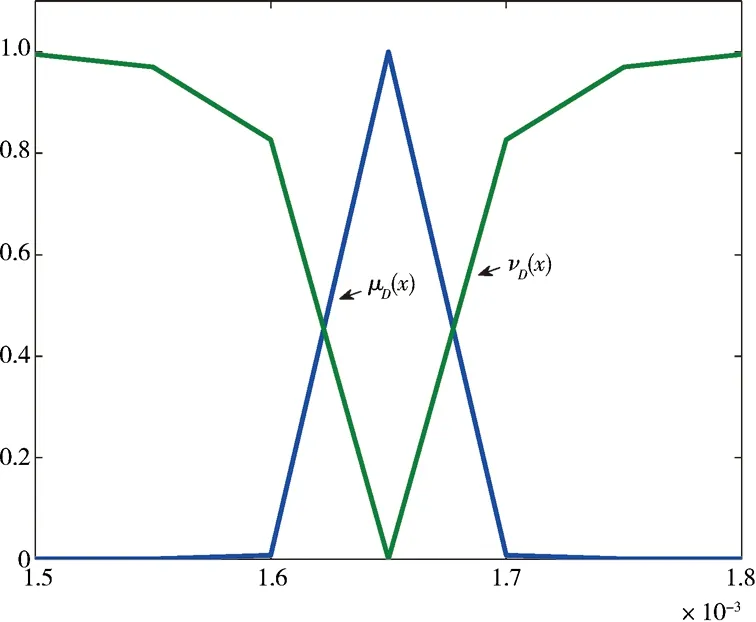
(b)D的隶属函数和非隶属函数的图像

图4C、D的隶属函数和非隶属函数的图像
Fig.4Thefiguresofmembershipandnon-membershipfunctionsofCandD

所以根据算法1可以分别得到正态型直觉模糊数C、E1、E2、H2、I1、I2、I3、Q、S和尖γ型直觉模糊数D、E3、H1、H3、K、O、R的三角直觉逼近:

T△(C)=(0.000 879,0.000 99,0.001 101;

0.000 879,0.000 99,0.001 101),

T△(D)=(0.001 627,0.001 65,0.001 673;

0.001 586,0.001 65,0.001 714),

T△(E1)=(0.001 591,0.002 2,0.002 809;

0.001 591,0.002 2,0.002 809),

T△(E2)=(0.000 548,0.000 77,0.000 992;

0.000 548,0.000 77,0.000 992),

T△(E3)=(0.000 529,0.000 55,0.000 571;

0.000 513,0.000 55,0.000 588),

T△(H1)=(0.000 528,0.000 55,0.000 572;

0.000 513,0.000 55,0.000 588),

T△(H2)=(0.002 064,0.002 97,0.003 876;

0.002 064,0.002 97,0.003 876),

T△(H3)=(0.001 08,0.001 1,0.001 120;

0.001 055,0.001 1,0.001 145),

T△(I1)=(0.002 531,0.003 3,0.004 069;

0.002 531,0.003 3,0.004 069),

T△(I2)=(0.002 441,0.003 3,0.004 159;

0.002 441,0.003 3,0.004 159),

T△(I3)=(0.001 847,0.002 42,0.002 993;

0.001 847,0.002 42,0.002 993),

T△(K)=(0.000 738,0.000 77,0.000 802;

0.000 695,0.000 77,0.000 845),

T△(O)=(0.001 165,0.001 21,0.001 255;

0.001 135,0.001 21,0.001 285),

T△(Q)=(0.003 792,0.004 4,0.005 008;

0.003 792,0.004 4,0.005 008),

T△(R)=(0.001 848,0.001 87,0.001 893;

0.001 842,0.001 87,0.001 898),

T△(S)=(0.003 411,0.004 18,0.004 949;

0.003 411,0.004 18,0.004 949).

根据图3，主要事件有如下的关系:

A=A1+A2+A3,E=E1+E2+E3,

F=F1×F2,

G=G1+G2+G3,H=H1+H2+H3,

I=I1+I2+I3,

J=J1×J2,M=M1+M2+M3,

N=N1×N2×N3,

其中正态型和尖γ型直觉模糊数用三角直觉逼近代替.用qi表示底部事件i的故障率,计算各个子事件的故障率如下:

qA= 1⊖(1⊖A1)⊗ (1⊖A2)⊗(1⊖A3) ≅

(0.005 762 5,0.006 918 4,0.007 695 1;

0.004 185 8,0.006 918 4,0.008 551 1),

qE= 1⊖(1⊖T△(E1))⊗ (1⊖T△(E2))⊗

(1⊖T△(E3)) ≅

(0.002 666 0,0.003 516 7,0.004 367 0;

0.002 650 0,0.003 516 7,0.004 384 0),

qF=F1⊗F2≅

(0.000 001 9,0.000 002 4,0.000 004 2;

0.000 001 0,0.000 002 4,0.000 005 4),

qG= 1⊖(1⊖G1)⊗

(1⊖G2)⊗(1⊖G3) ≅

(0.003 991 8,0.004 514 9,0.005 691 1,0.006 438 8;

0.001 022 7,0.004 514 9,0.005 691 1,0.007 524 7),

qH= 1⊖(1⊖T△(H1))⊗

(1⊖T△(H2))⊗(1⊖T△(H3)) ≅

(0.003 668 1,0.004 614 5,0.005 560 8;

0.003 628 2,0.004 614 5,0.005 601 6),

qI= 1⊖(1⊖T△(I1))⊗

(1⊖T△(I2))⊗(1⊖T△(I3)) ≅

(0.006 803 6,0.008 993 2,0.011 179 5;

0.006 803 6,0.008 993 2,0.011 179 5),

qJ=J1⊗J2≅

(0.000 008 6,0.000 012 2,0.000 014 1;

0.000 003 5,0.000 012 2,0.000 016 0),

qM= 1⊖(1⊖M1)⊗ (1⊖M2)⊗(1⊖M3) ≅

(0.005 996 3,0.007 470 1,0.007 798 4;

0.003 790 7,0.007 470 1,0.008 534 5),

qN=N1⊗N2⊗N3≅

(0.297 076×10-8,0.536 659 2×10-8,

0.674 205 6×10-8;

0.192 631 14×10-8,0.536 659 2×10-8,

0.973 026 6×10-8).

因为三角直觉模糊数是梯形直觉模糊数的特殊情况,所以各个子事件I、II、III、IV和V的故障率计算如下:

qI= 1⊖(1⊖A)⊗

(1⊖B)⊗(1⊖T△(C)) ≅

(0.007 739 1,0.009 092 1,0.009 588 1,0.010 552 0;

0.005 946 6,0.009 092 1,0.009 588 1,0.011 544 1),

qII= 1⊖(1⊖T△(D))⊗ (1⊖E)⊗

(1⊖F)⊗(1⊖G)⊗(1⊖H)⊗ (1⊖I)≅

(0.018 625 7,0.023 090 1,0.024 244 3,0.028 907 5;

0.015 603 4,0.023 090 1,0.024 244 3,0.030 066 5),

qIII= 1⊖(1⊖J)⊗ (1⊖T△(K))⊗(1⊖L) ≅

(0.001 805 6,0.001 991 2,0.001 991 2,0.002 494 9;

0.001 527 6,0.001 991 2,0.001 991 2,0.002 909 3),

qIV= 1⊖(1⊖M)⊗ (1⊖N)⊗

(1⊖T△(O))⊗(1⊖P) ≅

(0.009 715 9,0.011 347 7,0.011 585 6,0.012 075 9;

0.007 021 0,0.011 347 7,0.011 585 6,0.013 046 5),

qV= 1⊖(1⊖T△(Q))⊗

(1⊖T△(R))⊗(1⊖T△(S)) ≅

(0.001 805 6,0.001 991 2,0.001 991 2,0.002 494 8;

0.001 528 0,0.001 991 2,0.001 991 2,0.002 909 3).

那么顶部事件PCBA故障的可能性是

qPCBA= 1⊖(1⊖I)⊗ (1⊖II)⊗(1⊖III)⊗

(1⊖IV)⊗(1⊖V) ≅

(0.039 161,0.046 765,0.048 596,0.055 488;

0.031 294,0.046 765,0.048 596,0.059 269).

表5表示本文提出的方法计算顶部事件PCBA故障的可能性(当α=0,0.1,0.2,…,1时的隶属函数和非隶属函数的α-截集).文献[17]提出的方法只能计算系统部件故障率用三角形直觉模糊数表示的系统的可靠性,有很大的局限性.在实际应用中，系统部件用单一类型的直觉模糊数表示故障率这种情况很少发生,系统部件往往都是用不同类型的直觉模糊数表示其故障率的.文献[18]提出的方法虽然可以计算用不同类型直觉模糊数表示系统部件故障率的系统可靠性,但是首先得求出35个基本事件(当α=0,0.1,0.2,…,1时)的770个α截集,然后当α=0,0.1,0.2,…,1时再分别用区间的代数运算计算系统发生故障可能性,计算量比较大.本文提出的方法不仅可以对用不同类型直觉模糊数(可以包含一般直觉模糊数)表示系统部件故障率的系统进行可靠性分析,而且计算量小,计算结果的不确定性也比较小.文献[17-18]和本文提出的方法计算PCBA故障的可能性的模糊分布如表6所示.可靠性区间的长度越小,关于可靠性的不确定性就越小.从表6可以看到,本文用逼近的方法处理数据后,所得的结果有效地减少了可靠性区间的长度,即减少了模糊分布,比其它的计算结果更为精确.

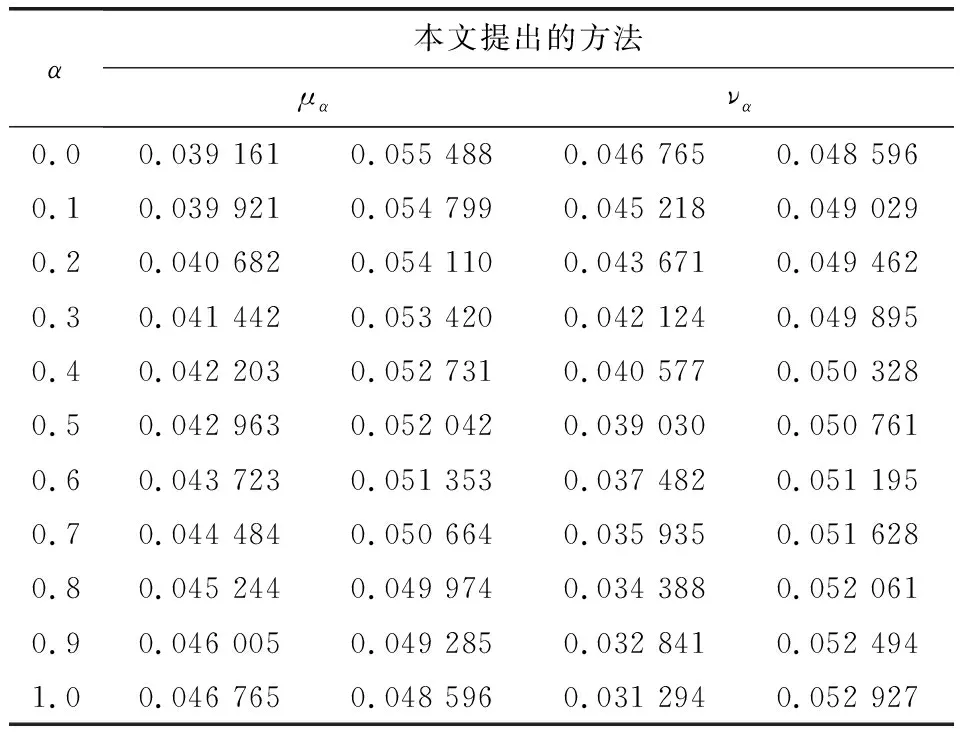
表 5 用本文提出的方法PCBA故障在不同截集水平的模糊故障率Tab.5 Fuzzy failure probability of PCBA fault at different level based on proposed method

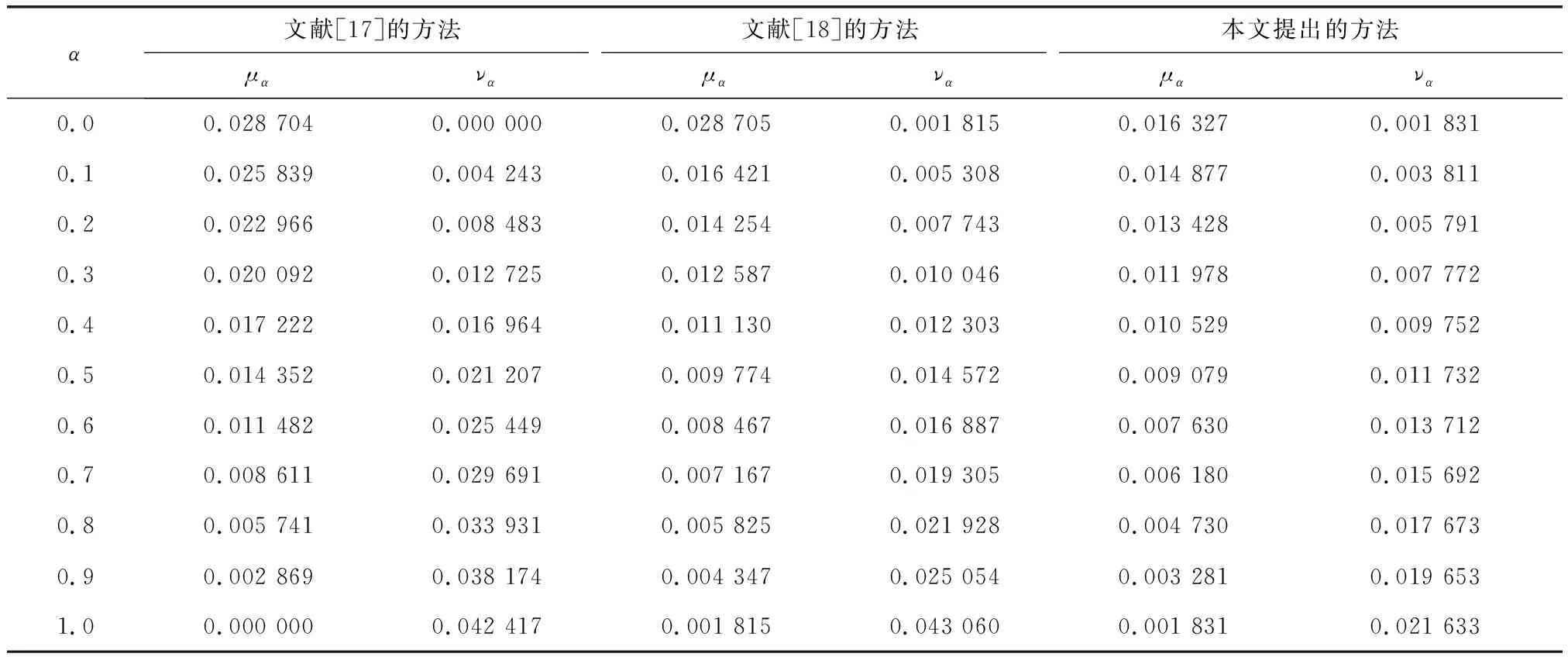
表 6 用不同方法PCBA故障的故障率的模糊分布Tab.6 Fuzzy spreads of failure probability of PCBA fault with different method

3 结束语

应用三角直觉逼近方法研究模糊系统的可靠性问题,对一个含有串并联结构的模糊系统,各个部件用不同类型的直觉模糊数表示其故障率,将正态型和尖γ型直觉模糊数都逼近成三角形直觉模糊数，然后用直觉模糊数的代数运算分析串联和并联模糊系统的可靠性.该方法解决了实际问题中遇到的系统部件故障率用不同类型直觉模糊数表示的模糊系统的可靠性问题,并且分析模糊系统的可靠性用的是直觉模糊数的代数运算,在一定程度上减少了计算量.最后通过PCBA故障分析表明,应用三角直觉逼近方法处理数据后,所得的结果与其它的计算结果相比较,有效地减少了模糊分布,提高了结果的可信度.

致谢海军大连舰艇学院科研发展基金对本文给予了资助,谨致谢意.