基于超声导波的管道缺陷量化评估仿真研究

梁伯翱,赵 锴,王晓娟,陈晓晓

(西安理工大学机械与精密仪器工程学院,陕西西安710048)

超声导波[1]是近年来新兴的无损检测技术。相对于传统的无损检测方法,它具有以下优势:①传播距离远,超声导波在固体中传播时沿传播路径上的衰减很小,可以在管道内传播很远的距离,最远可达上百米;②检测效率高,超声导波是线性检测,不是传统检测的点对点检测,大大提高了效率;③检测范围广,超声导波在管道的内、外表面和中部都有振动的质点,声场遍及整个壁厚,因此整个壁厚都可以检测到。早在上个世纪中期,外国学者已经开始对声波在管道中的传播进行理论研究。上世纪80年代,Silk和Bainton[2]利用压电超声传感器激励出超声导波,对电机管道的裂纹检测进行了实验,证明了利用超声导波技术检测管道的可能性。近些年,国内外的学者也开展了相关的实用化研究。何存富[3]开发出一种集成化的小型超声导波检测系统,该系统能够在管道中激励和接收超声导波,并通过对激励及反射回波的时空位置分析判断出管道长度和存在的缺陷。王智[4]重点研究了采用分布式PZT传感器在管中激励和接收特定模态超声导波的方法,并在此基础进一步研究管道缺陷回波的特性,通过分析、处理接收到的管道中的缺陷回波特征,达到缺陷识别和定位的目的。宋志东[5]分析了管道中的超声导波在传播过程中的衰减特性和缺陷反射特性,并通过L(0,2)模态和T(0,1)模态对含缺陷管道进行检测,指出纵向模态和扭转模态导波检可提供全部缺陷特征,并可以较为准确地对缺陷定位。

这些研究表明超声导波检测已经实现了对管道缺陷的识别和对缺陷的定位。但由于实际管道缺陷形态不规则,产生的反射回波信号往往很复杂,目前还不能实现管道缺陷的量化评估。本文针对此问题,通过有限元仿真方法研究超声导波与管道缺陷的交互过程,提出裂纹缺陷轴向尺寸的研究方法,提出利用缺陷前后沿分别产生的两个边界反射信号进行缺陷轴向尺寸的量化评估方法,并进一步通过有限元仿真验证了结论。

1 管道超声导波的有限元仿真

1.1 超声导波基础理论

波在管道中传播时,满足Navier运动方程[6]:

μ2u+(λ+μ)(

(1)

式中:μ和λ是管道材料的Lame常数,ρ是管道材料密度,u是位移场。

根据波动方程可进一步得到管道的频散方程,即与管道的内外径、密度、频率及波数有关的函数。频散方程的三种解对应导波的三种模态:纵向模态、扭转模态和弯曲模态,分别用L(m,n)、T(m,n)和F(m,n)表示,其中m和n分别表示周向和轴向模态参数,且均为整数。纵向模态和扭转模态为对称模态,弯曲模态为非对称模态。其中,纵向导波L(0,2)模态是所有模态中速度最快的,在管道检测时它能更快的到达接收端,因而可以更好地与其他模态进行区分,且L(0,2)模态在高频时,波速变化不大,频散现象不明显,这就使其在传播过程中衰减很小,可以到达更远的距离,同时波形图的幅值更大。另外,导波L(0,2)模态轴向位移相对较大,而周向位移分量相对较小,且位移分布相对均匀,所以L(0,2)模态导波对管道内外有一样的灵敏度。而T(0,1)模态传播速度保持恒定,无频散现象。这两种模态各有特点,在基于超声导波的管道检测应用中会根据检测需求考虑选择激励L或T模态,本文选择L(0,2)模态作为激励导波。

基于超声导波的管道缺陷检测过程见图1:通过交变电信号驱动压电陶瓷换能片,压电陶瓷由于逆压电效应发生机械形变从而在所处管道上产生机械波。这种机械波在管道内以导波形式传播,根据应力波理论,导波在遇到缺陷会发生反射、折射等现象并伴随模态转换,由接收端陶瓷压电换能片接收回波信号。在导波速度等信息已知的情况下,可通过分析回波信号实现对缺陷的检测与评估。

图1 超声导波传播示意图Fig.1 Illustration of guided waves propagating in pipeline

1.2 管道缺陷检测有限元仿真

有限元仿真分析主要包括三个过程[7]:前处理,求解计算和后处理。其中前处理主要是为求解计算提供准备工作,涉及到的操作包括定义分析类型、定义单元类型、设置属性参数、建立管道几何模型,并对建立的管道模型进行网格划分。求解计算主要包括施加边界条件、施加脉冲载荷、设置求解分析类型、确定载荷时间和载荷子步,并进行求解。后处理主要是从选取相关节点得到其位移时间关系,并进一步通过信号波形确定检测所需的相关信息。

研究超声导波和管道缺陷交互作用的有限元建模及分析的基本流程图见图2。

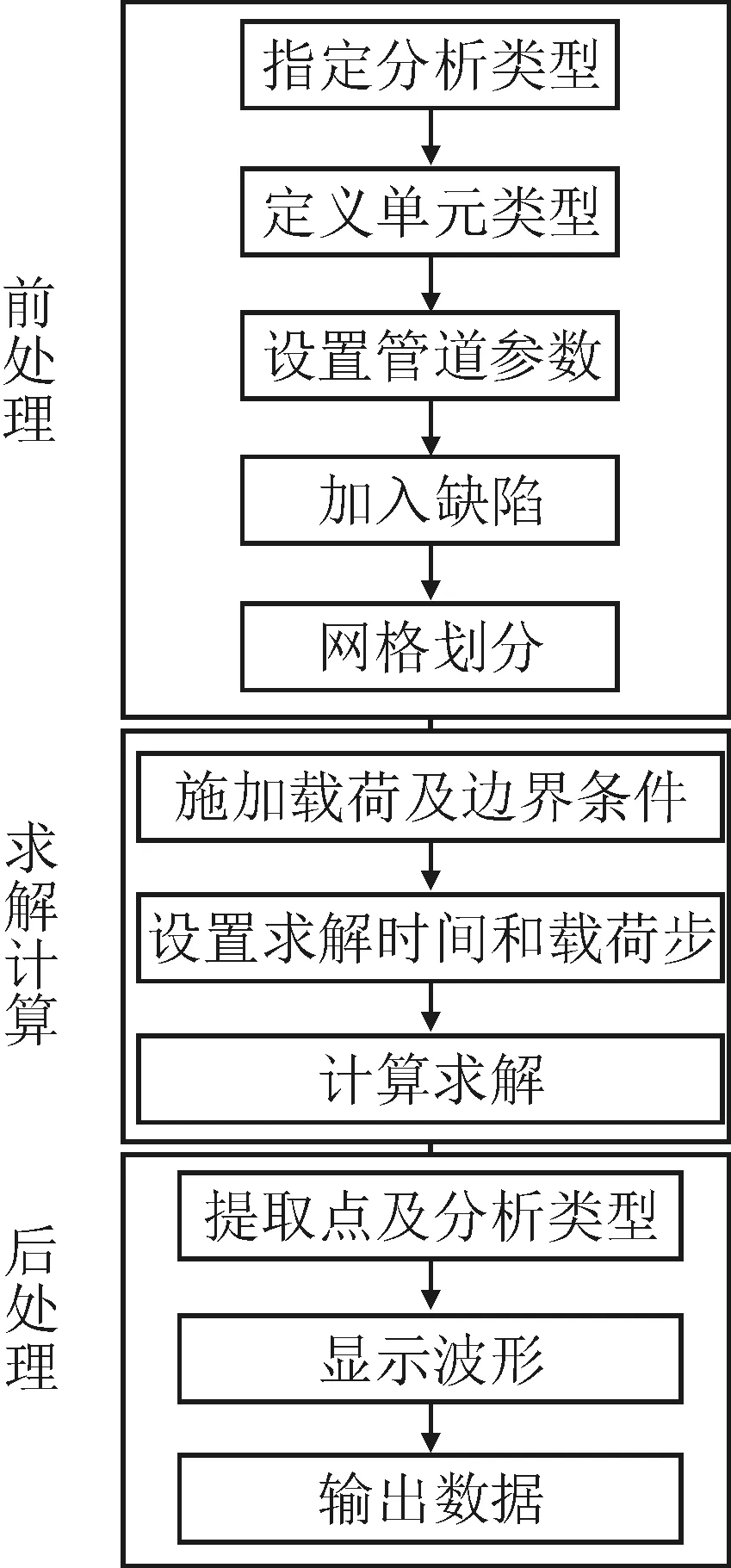
图2 管道缺陷检测有限元仿真流程图Fig.2 Flow chart of FE simulation of pipe defect inspection

1.3 有限元模型的建立及参数设置

本文分析讨论所用的管道有限元模型具体数据为:管道长度1 m,壁厚4 mm;缺陷距离管道端部0.5 m,径向深2 mm,周向宽360°,轴向长度在3 mm到180 mm范围内变化。管道模型的材料特性参数见表1。

表1 管道模型的材料特性参数Tab.1 Parameters of material property for FE pipe model

本文分析讨论的管道模型的频散曲线见图3,由英国帝国理工大学开发的Disperse软件绘制。由式(2)可得L(0,2)模态导波的理论波速为5 288 m/s。

(2)

式中:E为弹性模量,ρ为密度,ν为泊松比。

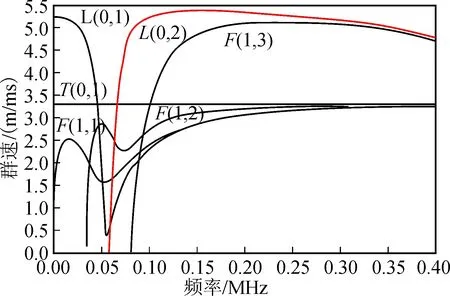
图3 本文管道模型的频散曲线图Fig.3 Dispersion curve of pipe model used in the paper

网格的划分和时间子步的选择是有限元模型建立的关键。对管道模型进行网格划分[8]须满足以下几个条件:轴向单元的长度小于激发信号波长λ的十分之一;端面网格划分与检测系统中传感器的周向分布一致或是其整倍数;此外,网格划分应保证计算精度满足要求而同时尽可能减少计算量。因此,根据本文建立的管道有限元模型的参数,选择网格划分单元类型为SOLID185,轴向单元长度2 mm,以保证仿真结果趋于稳定。

同时,总的仿真计算时间T须满足接收端至少接受到一次完整的导波反射信号:

(3)

式中,L为管道长度,Vg为导波在管道中传播的群速度。

时间子步ΔT必须满足:

(4)

式中,le是轴向单元长度。

管道模型的仿真参数见表2。

表2 管道模型的仿真参数设定Tab.2 Simulation parameter setting of FE pipe model

建立的有限元仿真模型见图4,由此模型得到的缺陷反射回波信号见图5。

本文讨论的仿真模型激励信号为L(0,2)模态,实际从缺陷产生的模态包括L(0,2)和L(0,1)模态。L(0,1)模态相比L(0,2)模态能量小且速度慢,因此下文只讨论分析主模态L(0,2)对应的缺陷回波。

图4 含缺陷管道的有限元仿真模型Fig.4 FE simulation model of pipe with a defect

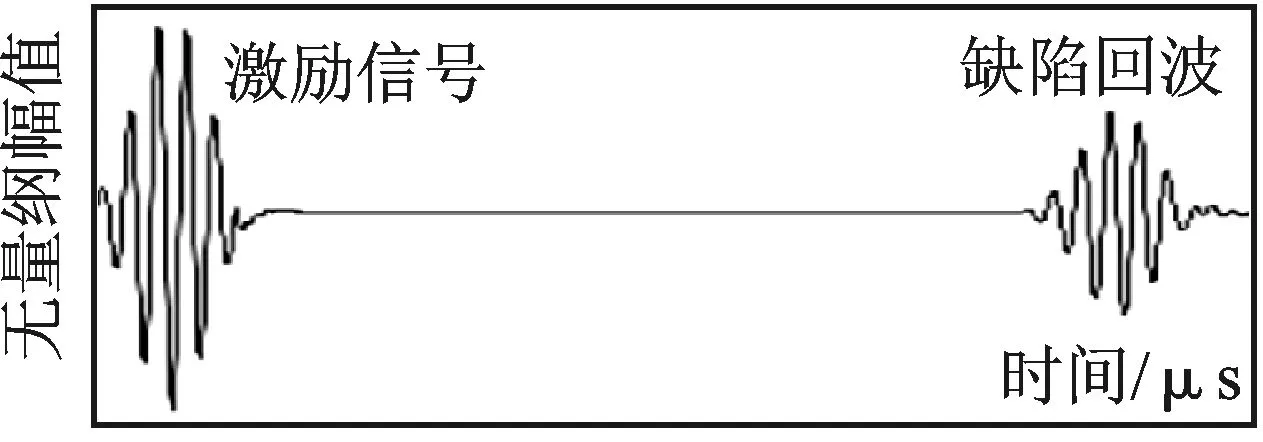
图5 仿真模型缺陷反射回波信号Fig.5 Defect reflectoin signal of simulation model

2 管道缺陷轴向长度的量化评估

为研究管道缺陷的量化评估,首先通过有限元仿真方法研究超声导波与管道缺陷的交互过程。本文重点考虑缺陷轴向长度,因此仿真研究的缺陷模型的三维尺寸中,径向深度和周向宽度保持不变,仅轴向长度变化。

仿真研究的结果发现,随着缺陷轴向距离的增大,回波信号逐渐分离(见图6)。在缺陷轴向长度为3 mm时,反射回波的波形与激励波形几乎相同,只是幅值产生减小;当缺陷轴向长度增大为3 cm、6 cm时,反射回波的包络线明显变宽;而增大至9 cm时,反射回波的波形逐渐分开为两个独立的波包,且波形与激励波形近似相同;至12 cm时,反射回波完全分离为两个波包。同时,在6 cm之后反射回波的两个波形基本分开。反射回波的第一个波包幅值不再变化,其形状保持一致;而第二个波包与第一个波包时间间隔逐渐增大,其幅值均小于前者,且呈现周期性变化。

分析可判断缺陷反射回波中包含的两个波包分别由缺陷的前后边界产生。当缺陷轴向长度较小时,前后边界产生的反射信号重叠在一起,形成缺陷反射回波;随着缺陷轴向长度的增大,前后边界产生的反射信号时间间隔增大,直至完全分离出两个波包。我们将前后边界反射信号完全分离时对应的缺陷轴向长度定义为临界轴向长度。前后边界反射信号和缺陷反射回波相比,缺陷反射回波模式更复杂,而边界反射信号与激励信号有更强的相关性,且能提供更多和缺陷尺寸相关的信息。

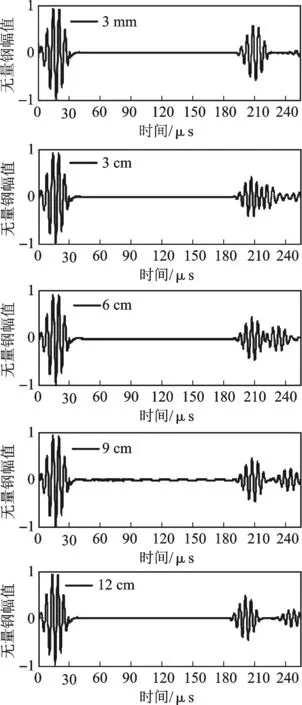
图6 不同轴向长度裂纹缺陷的仿真时程图Fig.6 Time-distance graph of different axial lengths of pipe defect

如前所述,管道缺陷的量化评估一直是导波检测中需要解决的难题。现有的评估方法一般都需要利用一定的基准信号作为参考实现缺陷的评估,且往往只能提供定性的评估结果。根据我们对超声导波与管道缺陷的交互过程的仿真研究结果,缺陷前后边界分别产生的反射信号可提供缺陷前后边界的对应信息,并进一步得到两边界间距,即实现对缺陷轴向长度的量化评估。缺陷轴向长度的量化评估主要涉及缺陷轴向定位和缺陷轴向长度的计算。

1) 缺陷轴向定位

缺陷定位是缺陷量化的第一步,同时也是很重要的一步。只有在缺陷定位正确的前提下,缺陷尺寸评估的研究才有意义。应用缺陷前后边界反射信号对缺陷进行轴向定位具体是指,通过导波传播至缺陷前边界再返回管道端面的时间和导波在管道中的传播速度,求解缺陷距离激励传感器的轴向距离,即实现缺陷的轴向定位,其示意图见图7。缺陷边界反射回波时间可由检测系统采集信号直接得到,导波传播速度可由频散曲线得到。轴向定位应满足如下公式:

(5)

式中,la是管道端面至缺陷处前沿的距离,tb是导波经缺陷前沿第一次返回至端面的时间,ta是导波在管道端面激励出波谷的时间,v是L(0,2)模态导波传播的速度。

图7 前后边界反射回波示意图Fig.7 Reflectoin signal at front and rear boundary

2) 缺陷轴向长度评估

利用缺陷前后边界反射信号评估缺陷轴向长度具体是指,通过导波分别传播至缺陷前、后边界再返回管道端面的时间和导波在管道中的传播速度,求解得到缺陷的轴向长度。轴向长度计算应满足下面公式:

(6)

式中,ld是缺陷的轴向长度,tc是导波经缺陷后沿第一次返回至端面的时间。

一般缺陷轴向长度的量化可首先通过理论计算得到缺陷前后边界分离的临界长度,在此基础上进行前后边界反射信号的分离,分离之后对时间信息进行提取,最后计算得到缺陷的轴向长度。

2.1 裂纹缺陷临界长度的确定

根据上文讨论,随着缺陷轴向长度的增加,前后边界反射信号逐渐分开。当轴向长度增大至临界轴向长度时,前后沿信号将完全分开。本文选取的激励频率为175 kHz,选取的激励信号是Hanning窗调制的5个周期的单音频正弦信号。临界轴向长度计算公式如下所示:

(7)

式中,v是L(0,2)模态导波的传播速度,t是周期。管道模型的临界条件参数见表3。

表3 管道模型的临界条件参数Tab.3 Parameters of critical condition for pipeline FE model

本文所得到的裂纹缺陷临界长度为75.76 mm,其导波波形见图8。

图8 临界轴向长度的时程图Fig.8 Time-distance graph of critical axial length

2.2 前后边界反射信号的分离

由上文可以知道,任何缺陷的反射回波都包含前后边界反射信号的成份。在图9(b)中可看到,轴向缺陷为10 mm时,前后边界反射信号是完全重叠的。如果要分析前后沿信号,首先就要将前后沿信号完全分离开来,得到单独的前后沿信号。

本文在有限元软件中分别建立缺陷轴向长度为10 mm和180 mm管道模型,两模型除缺陷轴向长度不同外,其它参数完全一致,前后边界反射信号可通过以下方法得到。

首先对轴向长度为180 mm的缺陷进行建模仿真,结果显示前后边界反射信号是完全分开的。

图9(a)中的第一个波包对应前边界反射信号f(1)。进一步对轴向长度为10 mm的缺陷进行建模仿真,这种情况下前后边界反射信号会重叠在一起,图9(b)中的第一个波包对应前后边界反射信号的叠加信号f(2),即缺陷回波信号。将信号f(2)与f(1)比较做差得到信号f(3),如图9(c)所示。第一个波包对应缺陷前边界反射信号,第二个波包对应缺陷后边界反射信号。

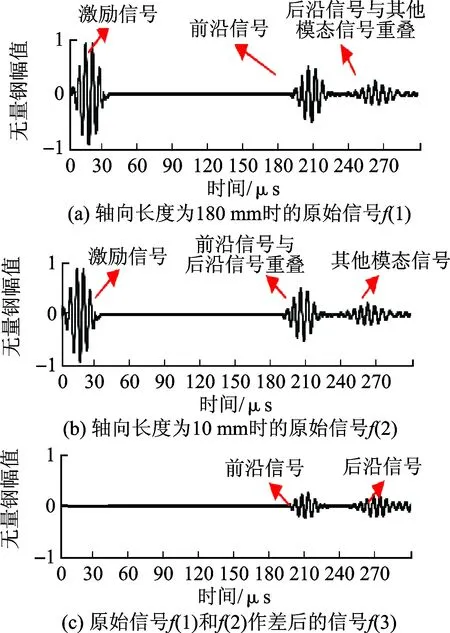
图9 前后边界反射信号分离过程Fig.9 Separation of front and back boundary signals

2.3 缺陷的轴向长度验证

图10为不同轴向长度缺陷的幅值变化,可以看到,缺陷轴向长度30 mm时,前沿幅值为0.43,其余前沿幅值均为0.46,说明前后边界反射波包逐渐分离后,前边界反射信号幅值能量保持不变,不受缺陷轴向长度的变化的影响。相对前边界反射信号的稳定,缺陷后边界能量的变化更为复杂。例如缺陷轴向长度30 mm时,后边界反射幅值为0.26,轴向长度增加至临界值时,后沿幅值减小0.21,90 mm时,又增大至0.24;120 mm时,又减小0.18,说明后沿能量变化的整体趋势随着轴向长度的增加而减小。同时,可以看出,前沿的幅值均大于后沿的幅值,即超声导波在管道传播过程中,前沿接收的能量更多。

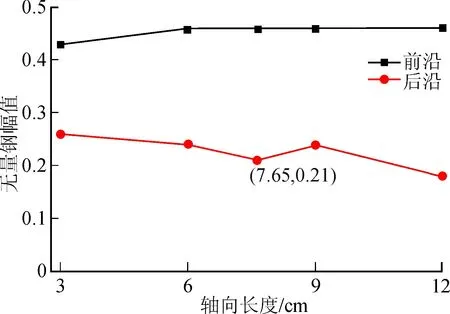
图10 不同轴向长度缺陷的幅值变化图Fig.10 Amplitude change for defects with different axial lengths

不同轴向长度缺陷的仿真结果见表4,可以看出,随着缺陷轴向长度的增加,超声导波从激励处传播至缺陷前后边界的时间间隔线性增大。仿真试验得出的轴向长度也越来越接近理论轴向长度,当理论轴向长度为10 mm时,仿真试验得出的轴向长度为11.14 mm,误差为11.14%,而当理论轴向长度为20 mm时,仿真试验得出的轴向长度为21.08 mm,误差为5.41%。继续增大理论轴向长度,所得到的误差减小至5%以下。当理论轴向长度达到100 mm时,所得到的误差为1.03%,精度达到98.97%。

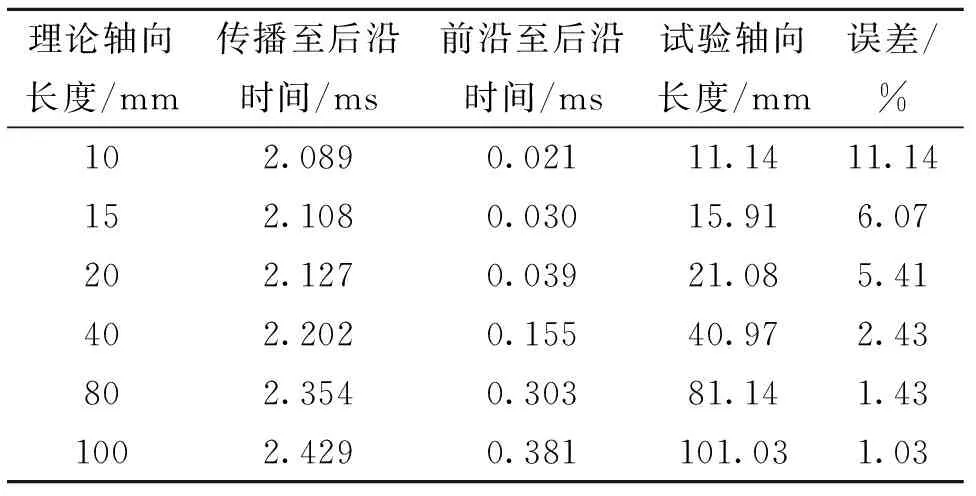
表4 不同轴向长度缺陷的仿真结果Tab.4 Simulation results for defects with different axial lengths

3 结 语

有限元仿真是研究超声导波的重要手段,本文通过有限元仿真方法研究超声导波与管道缺陷的交互过程,针对缺陷尺寸的量化评估问题得出了以下结论。

1) 提出利用缺陷前后边界反射信号进行缺陷轴向尺寸的量化评估方法。现有的评估方法一般都需要利用一定的基准信号作为参考实现缺陷的评估,且往往只能提供定性的评估结果。而根据缺陷前后边界分别产生的反射信号可提供缺陷前后边界的对应信息,并进一步得到两边界间距,即实现对缺陷轴向长度的量化评估。

2) 通过有限元仿真实验,利用仿真数据实现了从缺陷回波中分离出前后边界反射信号,验证了本文提出的可利用缺陷前后边界反射信号进行缺陷轴向长度量化评估方法。进一步的研究工作可在此基础上展开,如分离算法的构建和边界反射信号的进一步分析等,以实现缺陷尺寸的全面量化评估。