基于欧标的软弱岩地质条件下灌注桩承载能力设计分析
沈超,吴立柱,向军,吴中正
(1.中交第二航务工程勘察设计院有限公司,湖北 武汉 430060;2.中交二航局第三工程有限公司,江苏 镇江 212002;3.中交第二航务工程局有限公司,湖北 武汉 430060)
0 引言
桩基承载力计算对结构的重要性不言而喻,欧洲标准(EC7)[1]对灌注桩单桩承载力设计方法与国内标准大体相似,均可按照灌注桩桩侧摩阻力与桩端阻力的合力进行计算。就设计方法而言,EC7与国内标准区别主要在荷载组合选取上,在具体计算桩侧摩阻力、桩端阻力方面,EC7规范并未说明具体选取依据或者对应参数范围的推荐值,一般根据研究理论,通过土体或者岩石的相关试验结论进行推算。例如O’Neil和Reese对砂土和无黏性土进行了研究,并给出了对应的桩侧摩阻力计算公式[2],Williams和Pells给出了岩石的桩侧摩阻力计算方法[3];Vesic[4]、Meyerhof[5]等人均提出过对砂土和黏土等不同地质条件下桩端极限承载力的计算公式,并得到了广泛的采用。在桩基水平承载力设计理论上,本文将常用的Vesic方法与m法进行了对比。
1 欧标桩基设计方法
EC7规范在制定时为考虑统一性,包含了各国较通行的设计方法,因此在荷载组合选取上,根据不同国家的习惯存在几套不同的设计路径[6]。本项目所在地常采用英国有关标准进行水工结构的设计和施工,因此在组合上选用了设计路径一。由于桩基设计通常需要参考地质工程结果,并为结构设计服务,而结构设计须考虑极限承载能力及正常使用组合这两种工况,并在试桩时选取适当的组合和安全系数。因此,设计中不同组合需要同时考虑,这与国内标准的规定类似,区别在于欧标(英标)设计路径一在承载能力极限状态中采用了两套系数分别进行验算。
1.1 桩基竖向承载力设计
与国内桩基承载力的设计类似,桩基承载能力设计作用力与承载力之间的关系式见式(1)~式(3)。
式中:Fc,d为作用力设计值;Rc,d为承载力设计值;Gk表示永久作用和主导可变作用;Qk表示非主导可变作用;YG、YQ、YS和Yb分别为对应分项系数;Rs,k和Rb,k分别为桩侧和桩端的承载力标准值。
根据EC7中的有关规定,结构和地质设计依照设计路径一时,采用双系数A1+M1+R1和A2+M1/M2+R4对桩基承载力以及极限状态下的结构强度进行校核,其中A1、A2以及M1、M2分别表示设计路径一中两套组合的荷载分项系数和材料分项系数,而R1和R4则表示对应组合的抗力系数。然而,采用标准值组合对桩基竖向承载力进行评估时,所得到灌注桩荷载试验时需要的极限荷载通常是桩基承载力标准值的2~3倍。对应的欧标承载能力极限状态组合系数以及相应的抗力系数见表1和表2。
由表1和表2,欧标设计路径一的两种组合的系数各有不同,因此须分别计算,最后根据计算结果判断这两个组合中的一个为控制工况。与国内设计方法相比较可知,组合一荷载系数与国内行业标准[7]相近,但承载力分项系数值小于国内行业标准,而组合二荷载系数小于国内行业标准,承载能力分项系数与国内行业标准相近。

表1 荷载组合系数Table 1 Load combination coefficient
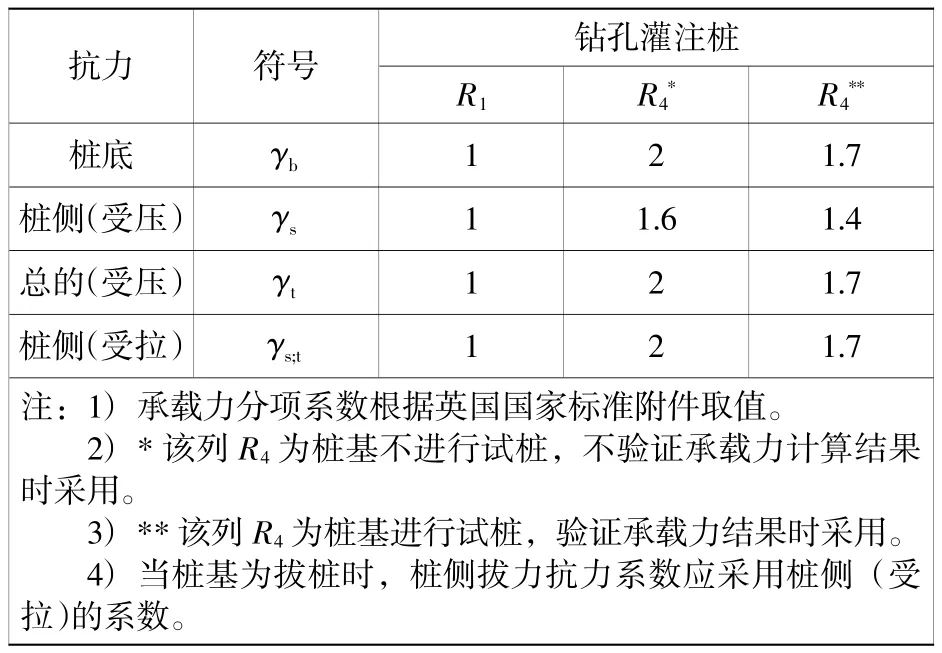
表2 承载力分项系数Table 2 Bearing capacity component coefficient
另外国内灌注桩承载力计算时,若桩径大于0.8 m还须考虑桩基的尺寸效应,在欧标中未提及对应要求,但在设计时除表2中承载力分项系数以外,还须根据工程地区常用的标准规范,考虑大于1的模型系数对桩基承载力进行折减。
在具体的桩侧摩阻力计算理论上,对于无黏土的桩侧摩擦力计算采用 O’Neil and Reese(1999)的β方法[2]。其中对砂土和碎石,桩侧阻力计算公式为:

式中:对于砂土 N≥15,取 β=1.5-0.007 7N < 15,β =N/15 (1.5-0.007 7)。对于碎石N≥15,取 β =2.0-0.000 82z0.75。
对岩石,桩侧摩阻力则根据Williams and Pells方法[3]进行计算,侧阻力计算公式为:

式中:系数α为单轴抗压强度折减系数;β为有关岩石裂隙间距的校正系数。这两个参数可根据岩石的RQD和单轴抗压强度进行推算。
桩端承载力相对于桩侧摩阻力,由于其需要较大沉降才能发挥,沉降量通常是桩尖直径的10%~20%,因此能够发挥岩石强度的承载力分量较小,尤其是长度较长的桩。另外,由于项目所在地岩质以形成时代较新的沉积岩为主,且软弱泥岩或砂岩混密实砂夹层(IGM)分布范围较广,不利于桩端承载能力的发挥,因此当地的设计惯例通常忽略端阻,于是上文中承载力计算式(2)修改为式(6)。

1.2 土体对桩基的水平作用
桩基受水平力作用时,国内常用嵌固点法、m法和P-Y曲线法,其中由于本项目桩基均在地表以下,并非高桩结构,若采用嵌固点法则误差较大,同时m法与当地常用方法相近,故本文选用该方法作为对比参照。
在水平反力计算中,土层模量系数nh由Reese和Vesic方法确定,对于砂土,nh是一个范围值,根据相应的表格可得到对应值;对黏性土和岩石,nh值被认为是一个常数,可以根据相关的理论进行推算,本文采用Vesic提出的方法,对桩侧水平弹簧劲度系数进行计算,具体见计算式(7)~式(9)。

式中:nh为土体模量系数;Es为土体压缩模量;μs为土体的泊松比;D为桩基直径;Ep为混凝土弹性模量;Ip为桩截面惯性矩;Kh为桩基水平反力系数;Ks为土弹簧劲度系数;I为沿桩身分布的土弹簧间距,常取1 m。
2 欧标桩基竖向承载力设计与国内行业标准对比分析
基于以上相关理论,对桩基承载力进行对比分析,土体参数按表3取值。

表3 土层分层和土体力学参数Table 3 Soil distribution and mechanics parameters
2.1 桩侧阻力计算结果对比
考虑到码头回填料新回填后会产生一定的沉降,同时桩基在受到卸船机往复工作的影响,上部土体会逐渐松散而减少侧阻力,因此海底面高程到码头后方回填标高范围内的回填料侧阻力未计入。另外桩侧摩阻力也会受到不同类型泥浆护壁的影响,如膨润土、聚酯纤维等。在回填料均不考虑桩侧摩阻力的情况下,计算得到的桩侧摩阻力和国内行业标准进行对比,见表4。
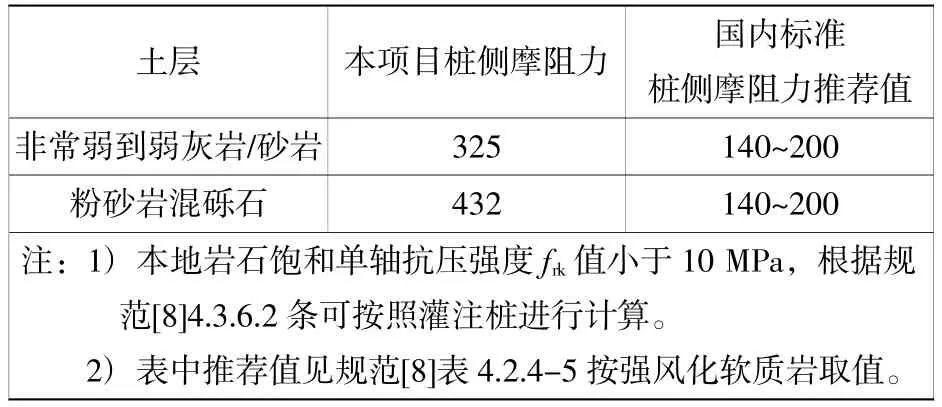
表4 桩侧摩阻力计算值与国标对比结果Table 4 Comparison results of computation value of pile skin friction forces with national kPa
按表4计算每米桩长桩侧摩阻力得到表5。
表5中计算桩径为0.9 m,根据国内行业标准,已考虑桩基的尺寸效应和受压桩轴向承载力抗力分项系数。另外,表5中计算值已包含欧标模型系数,取值为1.2。由表5可知,本项目欧洲标准设计路径一的两个组合参数的设计承载力计算值均大于按国内行业标准得到的计算值,其主要原因是国内行业标准推荐的经验值适用的土体范围较广(N63.5>10),相对于本项目理论计算值偏小,因此桩侧承载力结果偏安全。
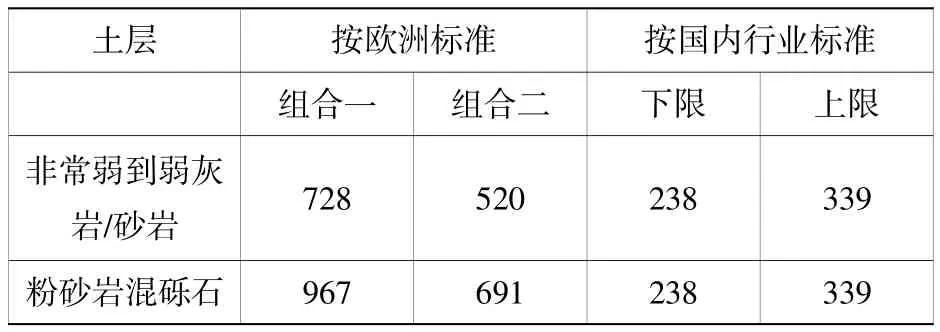
表5 欧洲标准与国内行业标准桩侧摩阻力结果对比Table 5 Comparison of pile skin friction forces between the European standards and Chinese standards kN/m
2.2 土弹簧劲度系数对比结果
对于桩侧水平弹簧系数的推算,由于国内行业标准[8]中并未给出对岩石的m值,项目当地的岩石RQD为40%~60%,因此参考了碎石土m值推荐范围计算每米土弹簧劲度系数,并将上下限进行分别绘图,得到曲线如图1所示。

图1 土弹簧劲度系数对比Fig.1 Comparison of soil spring stiffness coefficient
由图1中可知国内行业标准[8]推荐的m值计算的土弹簧劲度系数和用Vesic方法推算的结果相比较,基本能够将Vesic方法的结果包括在内,但规范推荐值上下限范围较大,而且随着入土深度增加,最大值和最小值的差值还有逐渐增大的趋势。
3 结语
本文对基于欧洲标准的灌注桩承载力设计方法进行了介绍,阐述了相关理论,并将对应的计算结果与国内行业标准进行了对比,发现在计算桩基竖向承载力方面,其基本方法是一致的,但是由于采用的桩侧阻力推算方法不同,且由于项目所在地岩质较软,灌注桩桩端承载力忽略的情况下,仅单纯对比分析了桩侧阻力,计算结果与国内行业标准相比有一定差异。国内行业标准由于推荐的经验参数较小,故在对比中偏安全。
在水平承载力计算方面,国内外的理论也基本相似,但对岩层水平土弹簧计算,由于需根据常用的理论进行计算,如Vesic等的方法进行推算,采用不同理论时计算结果会有不同。而国内行业标准计算m值的推荐值是一个区间,且上下两条折线包络的范围较大,因此也需要根据经验预判或者试桩结果进行取值。总体上讲本文采用的计算方法结果与国内m法基本趋势一致,且计算结果在国内行业标准的取值范围内。

