小型化快响应阀门装配工艺研究

刘 翔，袁晓东，刘 英，马瑞利

(西安航天发动机有限公司，陕西 西安 710100)

0 引言

小型化快响应阀门具有响应时间快，流量控制精确，质量和体积小等特点，但该类阀门零件特征尺寸较常规阀门大幅减小(多数零件的特征尺寸介于Φ2×15 mm与Φ15×30 mm之间)，因此加工中尺寸及形位公差难以控制，零件加工后尺寸偏差和形位公差增大，且装配时小型零件不易装配到位，会出现定位偏差增大的情况，当机加与装配的偏差累计过大时会导致阀门性能不满足设计要求的情况。要加工、装配出满足设计要求的阀门，需在平面尺寸链的基础上结合零件形位公差，构建三维装配尺寸链[5]，然后定位偏差产生环节，并制定合理的加工和装配方案。

1 装配尺寸链模型理论分析

装配尺寸链可直观体现阀门装配结构，其建立方法是先将各零件用空间向量代替，然后将空间向量依次连接，形成的封闭矢量环即为装配尺寸链模型。现以3个空间向量构成的空间尺寸链为例进行尺寸链分析说明，如图1所示，尺寸链的组成环大于3时分析方法一致。尺寸链中单一组成环AB，如图2所示。

图1 三维尺寸链Fig. 1 Three-dimensional dimension chain

图2 单一零件空间表达Fig. 2 Three-dimensional representation of single component

AB的空间表达，如式(1)所示：

AB=(|AB|sinαcosβ|AB|sinαsinβ|AB|cosα)

(1)

式中：|AB|为零件的基本尺寸；α为零件与Z轴的夹角；β为零件在XOY平面内投影与X轴的夹角。以上参数可通过蓝图获得。同理，其余向量的空间表达可通过同样方法计算得到，但需要注意建立坐标系之间的转化关系。

明确所有零件转化所得的空间向量的表达式后，能够计算封闭环AC的表达式，如式(2)所示。

AC=AB+BC

(2)

其中

BC=(|BC|sinαBCcosβBC|BC|sinαBCsinβBC|BC|

cosαBC)

式(2)结果为封闭环的理论表达形式，因零件加工和装配中均存在误差，所以需对式(2)进行修正。将其中参数|AB|，|BC|，α和β修改为|AB|+Δ|AB|，|BC|+Δ|BC|，α+Δα和β+Δβ，并带入式(2)，可得实际封闭环的空间表达式CA’，如式(3)所示。

CA′=(|AB|+Δ|AB||BC|+Δ|BC|)

(3)

理论封闭环和实际封闭环矢量差ΔCA即为封闭环的偏差，如式(4)所示。

ΔCA=CA’-CA=U·V

(4)

其中

U=(ΔαABΔβABΔαBCΔβBCΔ|AB|Δ|BC|)

由式(4)可知，封闭环偏差ΔCA由矩阵U和V构成，矩阵U是偏差源矩阵，其中元素是对封闭环偏差产生影响的因素；矩阵V是偏差敏感矩阵，其中元素表示相应偏差源的敏感程度。结合蓝图尺寸与形位公差数据可对偏差敏感矩阵V中各元素进行数值计算，敏感度大的偏差源对应的零件即为需在机加和装配中进行工艺控制的环节。

2 装配工艺分析

2.1 装配尺寸链建模与分析

具有代表性的小型化快响应阀门结构如图3所示。

1-螺母；2-阀杆；3-阀座 图3 阀门密封结构Fig. 3 Valve seal structure

此时阀杆(序号2)与阀座(序号3)接触保持关闭密封状态，阀门开启时阀杆与阀座分离，液体通过阀门进入下级。使用第1节装配尺寸链建模与分析理论对该结构进行分析，选取A,B和C三点作为装配点，再将阀杆、阀座使用空间矢量表示，依次连接空间向量后，形成空间装配尺寸链，如图4所示。

图4 阀门装配尺寸链Fig. 4 Assembling dimension chain of valve

其中AB为阀杆简化向量，BC为阀座简化向量，连接两处向量形成封闭空间尺寸链，其中自然形成的向量AC为封闭环。

图4中构成偏差矢量表达ΔCA的U和V矩阵可由第1节分析的计算公式得到，如式(5)所示。

U=(Δα1Δβ1Δα2Δβ2Δ|AB|Δ|BC|)

V=ABcosα1cosβ1ABsinα1cosβ1ABsinα1-ABsinα1sinβ1ABsinα1cosβ10BCcosα2cosβ2BCsinα2cosβ2BCsinα2-BCsinα2sinβ2BCsinα2cosβ20sinα1cosβ1ABsinα2sinβ1cosα1sinα2sinβ2ABsinα2cosβ1cosα2

(5)

式中参数意义及数值如表1所示。

表1 封闭环偏差矢量表达式参数意义及数值

使用表1中各变量数值进行计算,可得到计算结果如式(6)所示。

(6)

分析偏差影响矩阵V的计算结果可知，敏感度较大的两处为13.9和2.3，在偏差源矩阵中与以上两处敏感度对应的偏差源为Δα1和Δα2，即装配后阀杆相对于公共轴线a(图3所示)的同轴度及阀座上平面相对于轴线a(图3所示)的垂直度，因此需在装配过程中对阀杆和阀座的加工和装配环节进行控制。

2.2 重要密封面有限元分析

阀杆和阀座的加工尺寸、形位公差以及装配偏差均对阀门性能产生影响。装配后阀杆和阀座位于阀体内部，其密封状态可使用有限元分析软件进行模拟，直观得到正常密封及偏差较大非密封状态下阀座的密封锐边应变情况。

图5所示为阀杆同轴度与阀座垂直度满足设计要求时密封面受应力模拟结果，其中图5(a)为完整“阀杆—阀座”密封副显示状态，图5(b)为仅显示阀座密封面受应力模拟结果。由图5(b)可知，阀座上端密封锐边应变完整、均匀，选取锐边上4点读取应变值如表2所示，其应变值均匀，表明阀杆密封锥面与阀座密封锐边能够完全接触并产生均匀挤压，该状态下阀门密封性能良好。

图5 阀杆与阀座垂直度良好模拟结果Fig.5 Simulation results of valve spool and valve seat with good perpendicularity

图6所示为阀杆同轴度与阀座垂直度超差时密封面受应力模拟结果，其中图6(a)为完整“阀杆—阀座”密封副显示状态，图6(b)为仅显示阀座密封面受应力模拟结果。由图6(b)可知，阀座装配后阀座上端面密封锐边的所受应变不均匀，表明阀杆密封锥面与阀座密封锐边无法完全接触并产生均匀挤压，该状态下阀门密封性无法保证。

图6 阀杆与阀座垂直度偏差较大的模拟结果Fig. 6 Simulation results of valve spool and valve seat with poor perpendicularity

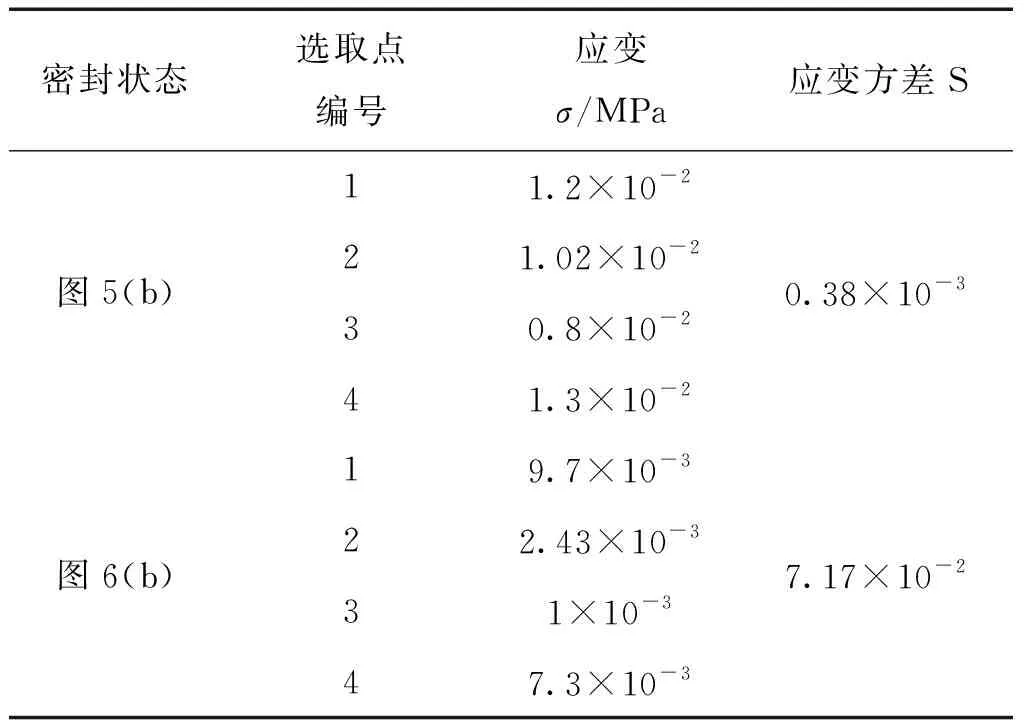
密封状态选取点编号应变σ/MPa应变方差S图5(b)11.2×10-221.02×10-230.8×10-241.3×10-20.38×10-3图6(b)19.7×10-322.43×10-331×10-347.3×10-37.17×10-2

3 零件加工及装配工艺设计

对阀座、阀杆的加工进行工艺设计，阀座加工中，其外形包含的外圆、内孔等特征需在一次装夹中加工完成，加工完成后对密封锐边使用20～40倍显微镜进行观察，要求密封锐边完整无缺口。阀杆属细长杆类零件，长径比为接近10，加工应力对该零件圆柱度影响较大，因此粗加工后先进行放置后再进行精加工。

阀门装配中也应对阀杆和阀芯的装配过程进行工艺设计，保证阀杆装配后与公共轴线a(图3所示)具有良好的同轴度，保证阀座装配后密封端面相对于公共轴线a(图3所示)具有良好的垂直度。阀门装配结构设计的装配流程如图7所示。

图7 小型化快响应电磁阀装配流程图Fig. 7 Assembly flow chart of miniaturized quick response solenoid valve

该装配流程中阀杆装配前密封元件、螺母、顶杆已完成装配，以上三处零件对阀杆起定位作用，后续压套、螺母起压紧、固定阀杆位作用，因此阀杆装配后易与公共轴线A保持较好的同轴度。阀座装配环节位于阀门装配流程的第2步，阀座装配前，阀体内部仅安装有两处密封元件，其余零件均未装配，如图8所示。

图8 阀座装配图Fig. 8 Assembling diagram of valve seat

阀座安装至阀体底部时需经过两处密封元件，所受摩擦力较大，且无可用于定位的零件，装配过程需在阀座上端持续施加较大轴向力才可完成装配。为保证阀座的可靠装配，设计了专用压杆对阀座进行装配，如图9所示，装配时先将阀座预装至图8状态后，使用阀座压杆将阀座垂直按压至阀体底部。

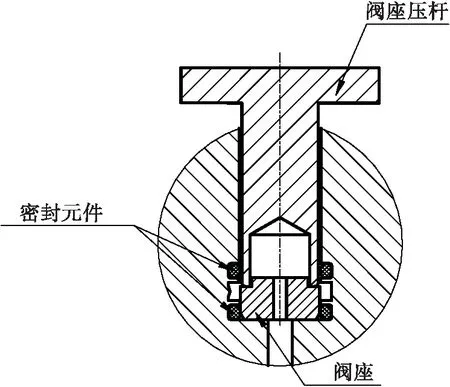
图9 阀座压杆使用示意图Fig. 9 Schematic diagram of valve seat with pressing bar

该装配过程阀座受到轴向定位，易通过密封元件安装至阀体底面，安装后可保证上端面与公共轴线垂直度在技术要求范围内，且密封锐边不受损坏。

4 零件加工及装配结果评价

对新制的阀座、阀杆的形位公差进行检测，结果如表3所示。

表3 零件形位公差表

使用新制的阀杆、阀座按照图7所示的装配流程进行阀门装配，其中阀座装配后采用20～40倍显微镜进行观察密封棱边，密封棱边清晰、完整、无缺口，未进行装配工艺设计时阀座装配后密封棱边存在损伤、缺口。

阀门装配后阀杆与阀座处的密封性如表4所示。

表4 阀座与阀杆密封性

由上述测量、试验结果可知，通过理论分析及根据理论分析专门进行的工艺设计能够对阀门零件生产、阀门装配进行指导，并且能够提高阀门装配后性能。

5 结论

小型化快响应阀门的内部结构紧凑，零件特征尺寸较小，加工偏差和装配偏差累计过大时会导致阀门出现不满足设计要求的情况。对于以上情况，首先将阀门装配结构转化为装配尺寸链模型，然后分析得到封闭环偏差源及其影响矩阵，使用蓝图尺寸计算封闭环偏差敏感度，针对敏感度较大的偏差源，需对相应零件的加工和装配过程进行工艺规划。使用该方法对某典型小型化快响应电磁阀的加工和装配过程制定了合理的工艺规划，满足了精微阀门的性能要求。