相同敏感值数据表泛化算法的安全性度量研究
郑明辉 杨晨 谭杰 吕含笑


摘 要:在k-匿名隐私保护策略的发展中,数据表的数据质量与安全性是相互制约的关系,在多样化敏感值数据表的隐私保护研究中,如何平衡数据质量与安全性之间的矛盾,也是备受关注的重点。但是,对相同敏感属性值的数据表进行泛化保护时,此方面的评价理论不适用于度量该类数据的可用性与安全性,文章针对这一不足,提出了一个基于熵理论的相同敏感值数据表泛化算法的评价方案。该方案引入了加权属性熵和链接匹配熵的概念,加权属性熵根据不同属性的重要程度计算数据损失量,链接匹配熵将链接攻击数据表消耗的正确匹配元组的信息量作为安全性度量。最后,利用提出的评价方案对两种泛化算法处理后的数据表进行评价,丰富了在相同敏感值条件下泛化算法的评价体系。
关键词:泛化算法;信息熵;信息损失量;链接攻击
中图分类号:TP3-05 文献标识码:A
Abstract: In the development of k-anonymity privacy protection, the relation between data quality and security is mutually restrictive. And in the research of multi-sensitive attribute value data, how to balance the contradiction between data quality and security is also the focus of attention. However, there works are not applicable for data with same sensitive attribute value. To solve this problem, we proposed an evaluation scheme of generalization algorithm for data with same sensitive attribute based on entropy. In this paper, weighted attribute entropy and linking matched entropy are introduced at first. Weighted attribute entropy individually calculates the amount of data loss according to the importance of quasi attributes. Linking match entropy measured the safety of algorithm by calculating the attackers information cost on correctly linked. Finally, the proposed evaluation scheme is used to evaluate the data tables processed by the two generalization algorithms, which enriches the evaluation system of the generalization algorithm under the same sensitive values.
Key words: generalization algorithm; information entropy; information loss; linking attack
1 引言
近年來在对数据隐私保护策略的研究中,平衡隐私泄露和数据可用性之间的矛盾关系是其关注的重点。隐私保护一直都是信息安全领域的热点问题,大数据时代的到来,使该问题更为突出和严峻[1]。数据挖掘的快速发展,容易导致用户的个人信息泄露[2]。k-匿名技术[3]常用作数据发布前的保护,其未来发展研究的重要内容包括如何精确评价公开数据表的安全性和信息损失量。
在隐私保护策略的发展中,不断有学者提出各种方法来度量数据可用性与安全性。Gionis等人提出了三种基于信息熵的信息损失度量方法[4],其缺点在于计算复杂,度量公式中的数值属性度量方法没有反映出泛化前和泛化后属性值之间的差异。李永凯等人根据属性选择性匹配问题,设计了匹配度量函数,并提出一个可以实现选择性匹配的隐私安全协议[5]。文献[6]利用聚类的质心与元组的距离表示信息的损失量。苏洁等[7]人提出了一种基于信息损失量估计的k匿名图流构造方法,实验表明所提方法能够较理想地控制信息损失量,缺点往往在于对网络图结构破坏比较大,使扰动后图数据的可用性较低。李钊等人提出一种基于扩展熵的信息损失量计算方法[8]。王芳等人[9]提出了一种基于局部划分的匿名算法,提高了数据匿名后的可用性,在减少信息损失量和提高关联关系保留率方面具有较高的合理性和有效性。
关于泛化算法安全性度量的相关研究,Domingo等人用元组之间成功链接的个数百分比、基于似然性方法的正确链接数的百分比以及原始数据落入泛化后区间的百分比来衡量安全性[10];吴振强团队[11]在单个属性的前提下对两个系统的匿名性进行对比,实用性不高;后又进行改进,文献[12]提出用联合熵作为匿名等级的评价指标,能够达到多属性系统的匿名性度量。Bertino等[13]人用匿名前后信息熵的改变来评估从不确定的数据集中获取一个确定值的难度,该值代表了数据集的安全性。Brickell等[14]人将泛化算法安全性的损失定义为攻击者从发布的数据中学习到新知识的量。张磊[15]等人从用户属性泛化的角度出发,提出了一种基于Hash 函数的泛化算法,并证明了该算法具备一定的隐私保护能力。熊平等[6]人把攻击者将某元组链接定位到一个最大等价类中,推断出该元组的敏感属性值的困难程度定义为泛化算法的安全性,适合于多样化敏感属性值的数据表,缺点在于层次聚类泛化算法的计算复杂度较高。文献[16]使用信息熵理论构造隐私量化模型,为隐私泄露风险的分析和度量提供理论基础。可以看出,在隐私保护中安全性的定义因安全性本身的抽象性而不同,如何用合适的参数量化安全性,还需视具体情况而定。在相同敏感值条件下,本文将泛化算法的安全性定义为攻击者利用微数据表链接出全集数据表中敏感信息的困难程度。
另外,值得关注的是k-匿名技术的研究始终建立在多样化敏感属性值的基础上,Liu Xiaoping等人[17,18]指出过度保护或欠缺保护是k-匿名技术在相同敏感值条件下泛化保护所面临的问题,但没有提出有效的算法安全性或数据质量的评价方案。鉴于合理的算法评价方案对于推进相同敏感属性值数据表的泛化算法是有帮助的,本文提出基于信息熵理论的加权属性熵和链接匹配熵,对相同敏感值条件下的数据损失程度和安全性进行计算,本算法不仅在泛化过程中保持了较优的等价类划分,保证了数据表在数据分析时能产生可靠的效用,且具有较高的安全性。
2 基于加权属性熵的数据损失量计算
相同敏感属性值的数据表省略了链接攻击时的敏感值定位过程,可以使用两个数据表模拟相同敏感值数据表的链接攻击。包含相同敏感属性值的数据表称为微数据表 ,全集数据表T用于链接攻击。本节将对相同敏感值数据表的可用性衡量进行分析。
定义1. 微数据表包含个准标识符属性,其权重为,包含条元组,对应的条元组中共有种数值,每种数值对应的元组为 ,表中每个的信息熵为:
微数据表的加权属性熵为:
定义2. 微数据表经泛化形成个等价类,用表示中符合取值区间元组的数量,用表示中等价类实际包含的元组个数,则泛化后微数据表加权属性熵为:
当微数据表被泛化为一个等价类时,各属性的熵值为0,数据表的可用性最低,因此加权属性熵越大,数据质量越高。准标识符属性的权重主要根据属性对敏感值的重要程度以及各属性值在划分区间的方差波动而定,可根据相关研究成果对准标识符属性进行权重设定,未对权重的精确性进行研究。
定义3. 微数据表中有个准标识符属性,其权重分别为,需满足:
3 基于链接匹配熵的泛化算法安全性度量
文中给出数据损失量的衡量标准,本节将在此基础上量化泛化算法的安全性,并给出相关定义。
3.1 相同敏感值数据表的安全性定义
在多样化的敏感值数据表受到链接攻击时,通常以攻击者推断出某条元组对应敏感属性值的难度作为衡量泛化算法安全性的标准。而在相同敏感值的条件下,攻击者的攻击难点在于正确匹配中的某些元组存在于中。
定义4. 相同敏感值条件下,攻击者利用链接出中一条元组敏感值的困难程度称为泛化算法的安全性。
3.2 链接匹配概率
相同敏感值条件下,攻击者链接多个数据表的目的是为了匹配出与共同的元组,同时还能获知中元组在中的额外属性信息。泛化算法的目的是确保在受到链接攻击时攻击者获取更少的敏感信息。
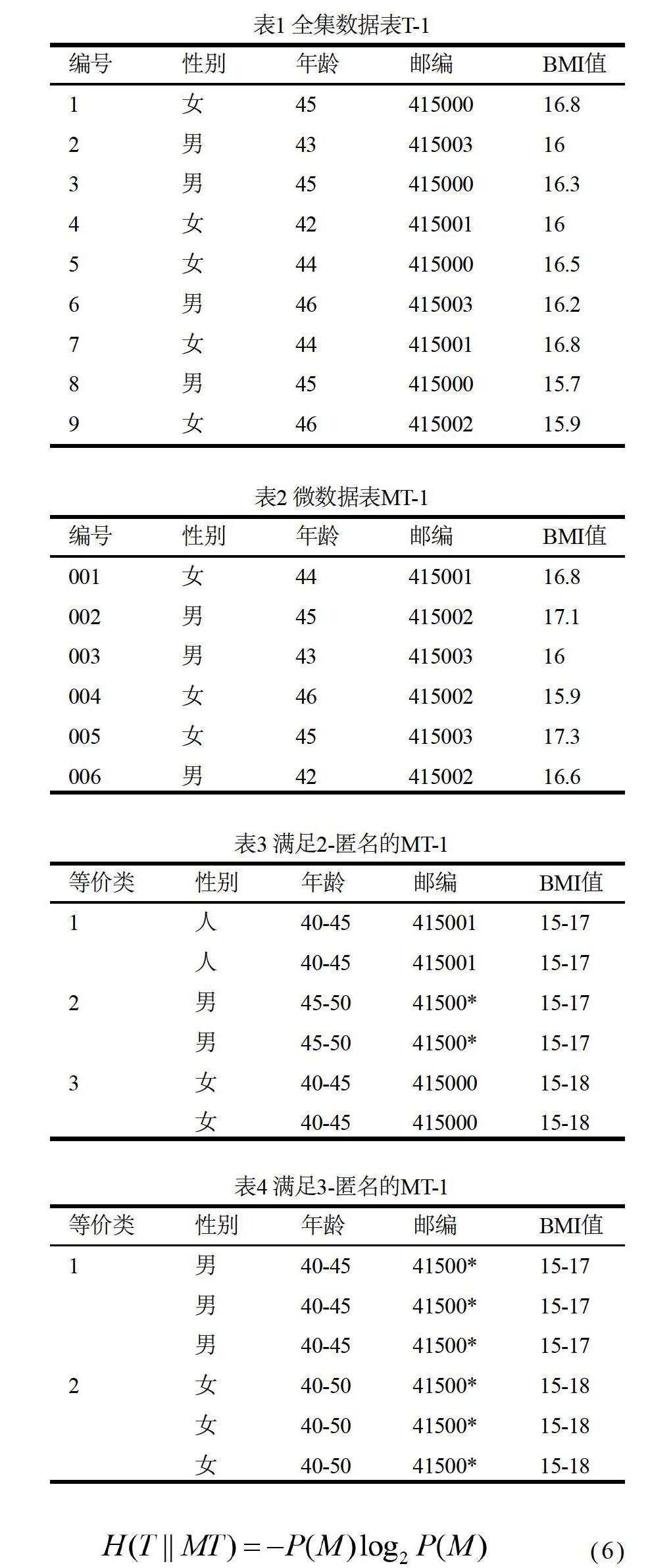
当的泛化层次越高,攻击者越难在链接攻击中正确匹配和中的元组。如表1所示,全集数据表T-1中含有4个准标识符属性、9条元组,表2是微数据表MT-1,表3和表4分别为满足2-匿名和3-匿名的泛化表。将表2与表1进行链接,可以推断表1中ID为2、7、9的元组以概率1存在于表2中,如表1、表2所示。将表3与表1链接,推断出ID为4、7的元组以概率1对应于等价类1,ID为3、6、8的元组以概率2/3对应于等价类2,ID为1、5的元组以概率1对应于等价类3,如表3、表4所示。将表4和表1链接,2、3、8元组以概率1对应于等价类1,1、4、5、7、9元组以概率3/5对应于等价类2。可以看出 中元组落入到各等价类的数量与微数据表的泛化程度有关,从而可计算中元组落入相对应等价类中的概率P。而的泛化程度越高,越难推断出中元组在中。
由于在不同泛化层次下中准标识符属性值所包含的信息量不同,攻击者则以不同概率获知中元组存在于中。因此可以用正确匹配元组的概率来表示泛化算法的安全性,将其定义为链接匹配概率。
定义5. 将中符合等价类取值区间的元组个数与等价类中元组数的比值定义为链接匹配概率。计算公式如下:
3.3 相同敏感值数据表的安全性度量
链接匹配概率是以攻击者的角度计算成功链接微数据表中元组的成功率,无需计算多条元组的泄露风险就能衡量攻击难度。
在与的鏈接过程中存在i个等价类,因此对应有i个链接匹配概率。衡量在链接攻击中的安全性可以通过计算这i个概率的熵来实现。
定义6. 链接匹配熵是指中本应落在已泛化的等价类取值区间上的元组数量与实际落入该等价类数量的比值P(M)的熵:
其中,T||MT表示与进链接匹配的过程。
链接匹配熵表示攻击者成功匹配元组所耗费的信息量。链接匹配熵越大,说明攻击者为实现匹配成功所消耗的信息量越多,即数据表的安全性越高。
3.4 基于信息熵的数据表安全性验证
泛化微数据表通过模糊化精确的属性值,使得攻击者要消耗更多的信息量才能得到泛化前的结果。由于链接攻击的结果不受各属性对数据质量贡献度的影响,所以算法的安全程度可以通过计算泛化前后的非加权熵之差来表示。泛化后的数据表信息熵反映的是泛化操作的效果,若该熵值越小,表示数据表包含的信息量越少,泛化程度越高,在链接攻击中越安全。
微数据表泛化前的信息熵为:
微数据表泛化后的信息熵为:
4 实验仿真
本节将使用加权属性熵和链接匹配熵对两种泛化算法下数据表的划分结果进行评价,实验数据选自数据库的数据。
4.1 准标识符属性权重设置
为便于实验进行,将数据集中14个准标识符属性降为7个。为不含“”敏感值的数据表,是从该数据表中选取的满足的近2300条元组成,保证了中的敏感属性值“”的范围是相同的。准标识符为{Race,Age,Hours-per-week,Education,Marital-status,Native-country,Gender},权重根据各属性的值在划分区间的方差波动程度进行设置,波动程度越大代表数据越不稳定,则赋予的权重相对较小,本节赋予准标识符属性的权重如表5所示。
4.2 不同算法的泛化操作分析
实验中将使用Liu Xiaoping等人提出的决策泛化算法和一种改进算法。在决策泛化算法中,将等价类泄露风险作为划分等价类的指标,泄露风险计算公式为:
(9)
其中,是中的元组个数(原算法以表示微数据表),表示划分后数据表的等价类数量,表示第个等价类中元组的数量,表示微数据表与全集数据表中第个等价类的元组数量之比。
决策泛化算法以表示每次划分后的第 个属性的泄露风险值,为第个属性中当前被分割的数据集的方差,可以针对性地对不同的准标识符属性实施划分。
改进后的算法称作加权泛化算法,本文算法在泛化数据表的全过程都有属性权重的参与,这一点不同于以前的算法。等价类划分的标准为:
(10)
决策泛化算法主要根据待划分前各属性的方差作为权重来划分等价类,当存在属性对数据可用性影响较小、但方差起伏较大的情况时,会更多以该属性作为划分等价类的标准,导致其他属性较少参与划分等价类的过程,使得泛化后数据质量会更低。如果提前对准标识符属性赋予权重,则会更细致地划分权重较大的属性,而即便对权重小的属性进行粗糙划分也不会对数据质量产生很大影响。
4.3 实验分析
如表6所示,将数据量控制为2300条元组,两种不同的泛化标准产生的不同的泛化结果。明显可以看出,在等价类数量上,加权泛化算法在划分时体现出优势;决策泛化算法的加权属性熵小于本文算法的熵值,说明在数据可用性方面加权泛化算法更优;链接匹配熵越大,攻击者要想攻击成功需消耗的信息量越多;而信息熵也验证了链接匹配熵的结果,因为信息熵是从微数据表包含的信息量角度证明了安全性,熵值越小则信息量越少,实验表明加权泛化算法的泛化程度更高,即更安全。
改变数据规模的大小,对实验进一步分析。如图1所示,加权属性熵反映数据表的数据质量,值越大越能反映数据的可用性。从图中可以明显看出随着数据量的变化,加权泛化算法的熵值明显优于决策泛化算法,原因主要在于各属性参与到划分等价类的过程中,因此总是优先划分权重最高的属性,确保数据分析时数据的可靠性和安全性。
如图2所示,利用泛化后数据表的信息熵的变化,来反映两种泛化算法对应的抵御链接攻击的能力。可以看出两种泛化算法得到的数据表信息熵,随着数据规模的增大都呈现出近似线性增长的趋势,而决策泛化算法泛化后的数据表信息熵始终高于加权泛化算法,这也表明决策泛化算法所得数据表信息量要相对大一些,也就是说,加权泛化算法的安全性更高一些,抵御链接攻击的能力更强。本算法不仅在泛化过程中保持了较优的等价类划分,保证了数据表在数据分析时能产生可靠的效用,且具有较高的安全性。
5 结束语
本文就相同敏感属性值条件下微数据表的泛化算法提出了衡量数据表损失量与安全性的度量方案,以加权属性熵量化数据损失量,以链接匹配熵量化算法安全性。在仿真实验中将属性的权重作为改进等价类划分标准的因素,解决了泛化时利用方差作为权重导致的等价类划分不合理的问题,提高了泛化后数据的可用性。本文对不同的泛化结果进行对比,完善了相同敏感值条件下数据表的评价体系。但目前实验没有就等价类中元组数量k值进行不同取值的实验,因此未提出全面的评价标准。后续拟对评价标准进行研究,力求达到可量化任一种泛化算法对相同敏感值数据表泛化保护后的数据损失量以及安全性。
参考文献
[1] 王威,李楠.大数据时代个人隐私防范与保护策略研究[J].网络空间安全,2017,8(Z2):9-13.
[2] 冯登国,张敏,李昊.大数据安全与隐私保护[J].计算机学报, 2014,37(1):246-258.
[3] LATANYA SWEENEY. k-ANONYMITY: A MODEL FOR PROTECTING PRIVACY[J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2002, 10(5):1-14.
[4] Gionis A, Tassa T. k-Anonymization with Minimal Loss of Information[M]. IEEE Educational Activities Department, 2009.
[5] 李永凯,刘树波,杨召唤,等.MSN中用户属性隐私安全的选择性匹配协议[J].华中科技大学学报(自然科学版), 2015(5):89-94.
[6] 熊平,朱天清,顾霄.基于信息增益比例约束的数据匿名方法及其评估机制[J].计算机应用研究, 2014,31(3):819-824.
[7] 苏洁,刘帅,罗智勇,孙广路.基于信息损失量估计的匿名图构造方法[J].通信学报,2016,37(06):56-64.
[8] 李钊,孙占全,李晓,等.基于信息损失量的特征选择方法研究及应用[J].山东大学学报(理学版),2016,51(11):7-12.
[9] 王芳,余敦辉,张万山.基于局部划分的匿名算法研究[J/OL].计算机应用研究,2019(11):1-3[2019-06-12].
[10] Domingo-Ferrer J, Torra V. A quantitative comparison of disclosure control methods for microdata[J]. Confidentiality Disclosure & Data Access, 2001.
[11] 吳振强,马建峰.基于条件熵匿名模型的优化[C].中国密码学学术会议,2004.
[12] 吴振强,马建峰.基于联合熵的多属性匿名度量模型[J].计算机研究与发展,2006,43(7):1240-1245.
[13] Bertino E, Fovino I N, Provenza L P. A framework for evaluating privacy preserving data mining algorithms[J]. Data Mining and Knowledge Discovery, 2005, 11(2): 121-154.
[14] Brickell J, Shmatikov V. The cost of privacy: destruction of data-mining utility in anonymized data publishing[C]//Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2008: 70-78.
[15] 张磊,王斌,于莉莉.基于Hash函数的属性泛化隐私保护方案[J].信息网络安全,2018(03):14-25.
[16] 彭长根,丁红发,朱义杰,等.隐私保护的信息熵模型及其度量方法[J].软件学报,2016,27(8):1891-1903.
[17] Liu X, Li X, Motiwalla L, etal. Sharing patient disease data with privacy preservation[C].Ais Sigsec Workshop on Information Security and Privacy. 2015.
[18] Liu X, Li X B, Motiwalla L, etal. Preserving Patient Privacy When Sharing Same-Disease Data[J]. Acm J Data Inf Qual, 2016, 7(4):17.

