结合Tikhonov正则化方法的近红外漫射光血流成像技术
张晓娟,徐金荣,桂志国,白馨,左佳,刘祎,尚禹
1. 太原工业学院 电子工程系,山西 太原 030008;2. 中北大学 信息与通信工程学院,山西 太原 030051
引言
近红外漫射光谱(NIRS)是一种无创检测生物组织血氧含量的技术,为脑部缺血、骨骼肌痛和肿瘤等疾病提供诊断依据[1-3]。将NIRS技术扩展至成像领域,即漫射光学层析成像(DOT)技术,可以根据病变组织中氧含量与周围组织的对比度,准确定位病灶位置[4-7]。测量的血氧含量,包括氧合血红蛋白、脱氧血红蛋白和总血红蛋白浓度,可以评估组织氧供给量之间的平衡关系,是个静态指标。血氧是通过血流对组织内血细胞进行氧气供给的,血流变化可以动态反映组织微血管系统中血液动力变化趋势。因此,血流的相对变化可以更早、更有效地预测疾病的产生与发展。
近年来,一种“动态”NIRS技术,即漫射相关光谱(DCS)技术快速发展,已经用于组织微血管血流变化的监测中。DCS技术利用光场的时间自相关函数(g1(τ))计算红细胞的运动状态,进而无创地监测微血管中血流随时间的变化值[8-9]。将DCS扩展至成像领域(DCT),就可以得到血流的空间图像[10-11]。
与DOT技术类似,早期的DCT重建算法也是基于解析解的,同样受限于组织的几何形状。最近几年,有限元方法(FEM)也引入了DCT,并且已经应用在乳腺癌检测中[12]。这两种算法已经成为DCS和DCT的主流数值技术,但两者共同的缺点是只能用自相关函数(g1(τ))曲线上的某一点作为原始数据进行重建,这将严重影响血流重建的精确性和稳定性。
在对当前方法深入分析的基础上,本文引入了一种新型的N-阶线性算法(NL算法)来实现血流成像。与传统的解析表达式和有限元方法不同,NL算法不寻求偏微分方程的解,而是将g1(τ)的积分形式与其N阶泰勒多项式相结合,并且通过光在组织内的传输信息来体现组织的非均匀性和不规则性[13]。此外,该算法还充分利用了多个时间点对应的g1(τ)值进行血流重建,这样,可以有效增加图像重建的准确性和稳定性。
将N-阶线性算法应用到DCT血流成像中,由于测量数据远远少于待重建的图像体素,其对应的线性方程组呈严重病态,因此,本文引入Tikhonov正则化方法进行图像重建[14-15]。本文通过计算机仿真,在真实的磁共振人体头部模型中进行了仿真验证,重建过程中所需的光子路径信息由蒙特卡罗仿真提供[16-17]。
1 方法
与DOT成像技术类似,DCT也需要在待测组织的表面放置若干光源—探测器(S-D)组合,用于收集逸出组织的光子,然后根据光子的自相关曲线进行血流的三维重建。
1.1 组织模型建立与S-D放置
本文采用的组织模型来自于开源的磁共振(MRI)数据库(http://brainweb.bic.mni.mcgill.ca/brainweb/)中正常成人头部影像。由MRI影像重建的头部可视化模型如图1a所示,光学探头(包含S-D的光纤)放置于前额(蓝色区域)。S-D的位置如图1b所示,红色为光源,共9个;黄色为探测器,共28个。每个光源发出的光子可以被任何一个探测器检测到,因此共有252个S-D组合。光源和探测器的标号顺序为从左往右,从下往上。
整个头部模型的大小为18.1 cm×21.7 cm×18.1 cm,X、Y、Z的间隔均为0.05 cm,因此共有362×434×362个单元,这远远大于测量数据的个数(即252个S-D组合)。考虑光子对组织的入射深度和逸出范围,取S-D覆盖部分3 cm×3 cm×3 cm局部区域作为图像重建的范围 (即图1中蓝色阴影部分)。为进一步减少单元个数,将这部分区域重新抽样,使体素大小为0.2 cm×0.2 cm×0.3 cm,则该局部区域单元个数缩减为15×15×10=2250个。为了检验算法的有效性,设置了两种异常血流状况(图2~3):一种是“十字形”异常血流组织,包含10个组织单元,图2a为含“十字形”异常血流的头部立体模型,图2b为X-Y横切面,图2c为选定区域X-Y横切面;另一种是“双条形”异常血流,包含4个组织单元,图3a为含“双条形”异常血流的头部立体模型,图3b为X-Y横切面,图3c为选定区域X-Y横切面。正常组织的血流值设为1×10-8cm2/s,异常组织单元的血流值设为5×10-8cm2/s,即异常组织的血流值为正常组织的5倍。
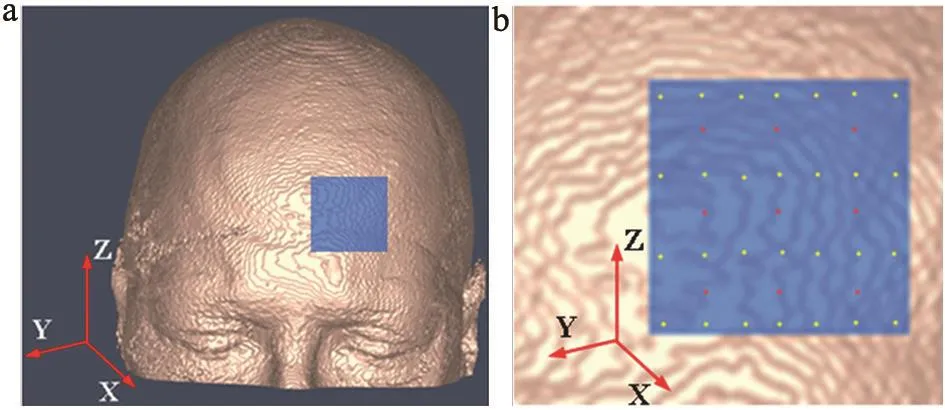
图1 MRI影像重建的头部可视化模型(a)及光源探测器放置位置(b)
1.2 MC仿真与自相关函数g1(τ)的计算
本文利用MC仿真(MCVM)来模拟光子在脑部的传输轨迹[15],从而得到每个S-D组合检测的光子数和光子传输路径。光子MC仿真的参数设置如下:吸收系数μa=0.1 cm-1、散射系数 μs=80 cm-1、各项异性因子 g=0.9,折射系数n=1.4[15]。每个光源约107个光子出射,探测器采集到的光子信息包括光子坐标、传输方向、路径长度和权重(即光子能量),这些信息用于计算光斑强度的自相关函数 g1(τ)。

其中P(s1,…sn)为光子传输路径在n个单元中的归一化分布,k0(i)为第i个单元的光波矢幅值,表示光子在第i个单元中的随机步长,该值等于1/μs'(i),τ为自相关函数的延时。<Δri2(τ)表示第i个单元中散射粒子在时间段τ内的均方位移,其形式取决于具体的流动模型,根据以往的研究,布朗运动模型与实验数据吻合较好,即 <Δri2(τ)>=6αDB(i)τ。α为运动粒子与总粒子数的比值,αDB定义为生物组织中的血流值(BFI)[13-14]。
为了更有效地接近实际测量,在产生自相关函数g1(τ)的同时,加入了噪声[8],得到了含噪声的自相关曲线,并利用含噪数据进行了血流重建。
1.3 N-阶线性算法
将g1(τ)展开为N阶泰勒级数g[13]:
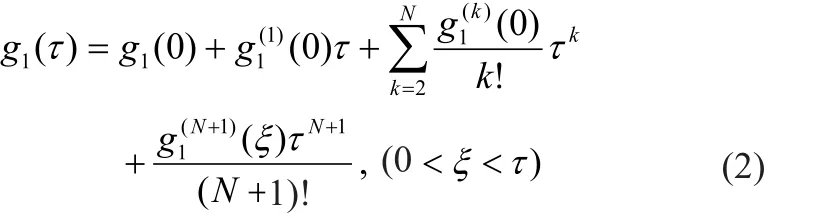
并结合式(1),可以得到一阶(N=1,公式(3))和N阶(N>1,公式(4))的关于g1(τ)的展开式 :

对 g1(τ)的 一 阶 近 似 式 (3),即为第j个S-D的相关曲线g1(τ,j)-1关于时间τ的斜率,表示为Sl(j)。
令A=CT,则血流值BFIs(αDB)可以直接由式(6)给出:

这 里,αDB=[αDB(1),…, αDB(n)]T,A=A(i,j)m×n,Sl=[ Sl(1),…, Sl(n)]T。
对g1(τ)的N阶近似式(4),由于方程两边均出现了αDB,因此需用迭代的方法进行求解:

公式(6)和(8)即为图像重建的关键理论支撑[13-14]。
1.4 图像重建方法
令X=αDB,B=Sl,则公式(5)和(7)可以由线性方程(8)表示:

这里,A=A(j,i)252×2250为所有S-D(共252组)针对所有组织单元(共2250个组织单元)得到的系数矩阵,X2250×1为 2250个组织单元,B252×1为得到的 252 条 g1(τ)曲线斜率,对这种严重不适定问题,一种较为有效的计算方法就是在求解过程中利用某些先验信息进行约束,Tikhonov正则化方法即利用2-范数[16-17],将问题转化为:

X0为均匀组织的血流值BFIs(αDB)。λ是平衡线性方程组与惩罚项权重的正则化因子。Tikhonov迭代算法的公式如下所示:
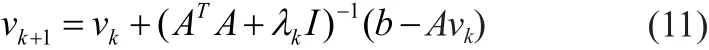
这里,λ0, λ1, … ,λk一系列正则化因子,λ0为首次迭代的正则化因子,采用通常的方法,将L曲线的拐点作为λ0[18-19],λ1, … ,λk则通过公式 (12)迭代得到 :
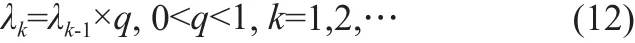
通过使用这种非平稳迭代方法,vk更接近最优解,收敛速度更快。Tikhonov正则化的伪代码如下:
给定:A,b,初始化:v0=ATB(反投影方法),λ0取值为L曲线的拐点,设定迭代的条件,计算:

非负约束:

更新:

另外,由于组织的厚度和S-D的距离问题,某些组织单元中只有很少的光子经过,使用这些数据将对图像重建带来不稳定性,所以,我们将组织单元中光子数少于15的单元剔除。这样,2250个原始单元减少至1424个;得到的线性方程组为 A252×1424X1424×1=B252×1。重建完成后,剔除掉的单元以均匀组织的血流值(1×10-8cm2/s)补充。
2 结果分析
本节主要阐述了N-阶线性算法结合Tikhonov正则化对选定组织区域的重建效果,在含噪声和不含噪声的条件下,分别对“十字形”和“双条形”异常BFI进行了重建,并通过均方根误差(RMSE)对重建效果进行了客观评价。
2.1 不同形状异常BFI重建效果
Tikhonov正则化算法重建的结果由图2和图3所示。

图2 “十字形”异常血流值位置建模和重建效果图
可以看出,不含噪声的血流图像重建效果精确程度高,噪声显著影响图像重建的质量,尤其是深度较大的血流异质物。但是,无论是否有噪声,都可以清楚地判断出异常血流组织的形状和位置。例如,“十字形”异常血流的形状可以辨别出来(图2)。对于异常血流的位置,Tikhono-DCT算法也区分出了距离仅为0.4 cm的两个条形异常血流组织,即使两个条形异常组织的宽度只有0.2 cm,也可以精确重建(图3)。
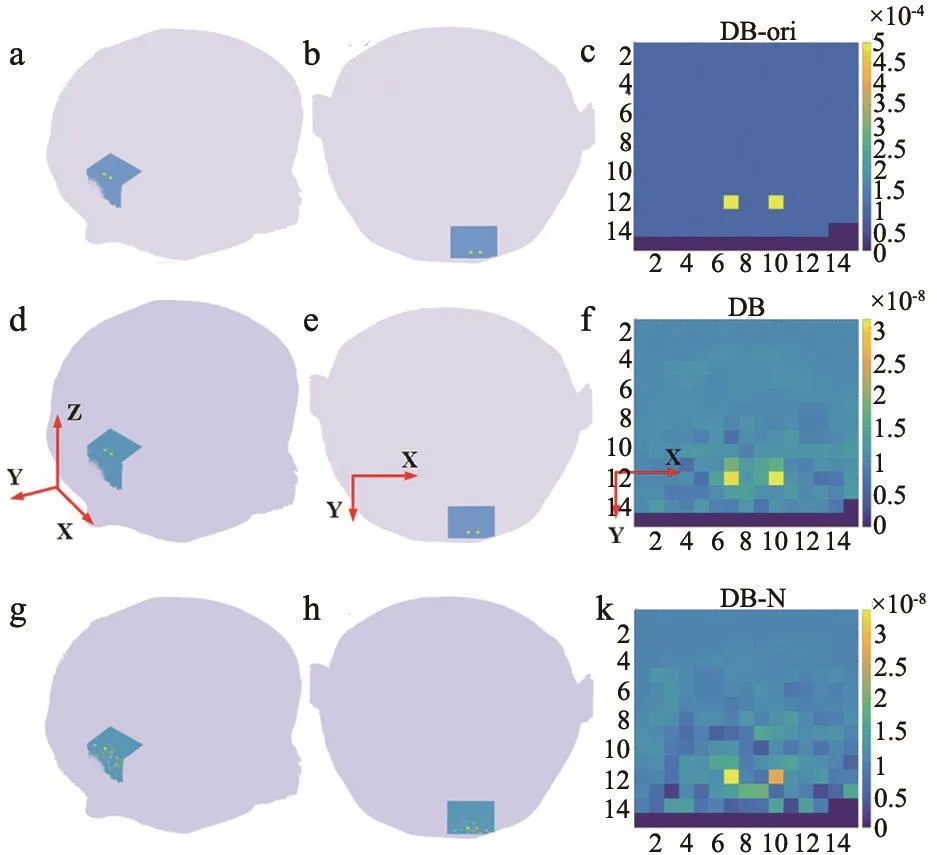
图3 “双条形”异常血流值位置建模和重建效果图
通过定量分析,不含噪声的重建图像中,重建的最大异常值为4.65×10-8(接近真实的异常值(5×10-8))组织位于图像正中间,边缘部分逐渐减小,如图2f所示。含噪声重建的血流图像,最大异常值为3.93×10-8,精确性有所降低,这符合常识。本次试验为五次加噪之后的平均值,测试次数越多,均值越稳定,但是耗时越长。
2.2 均方误差评价标准
为了对图像重建效果进行定量分析,我们使用了均方根误差方法,如式(16)所示:

均方根误差反映了重建图像与原图像的相似度,该值越小,图像重建效果越好。异常组织深度增加,重建图像的RMSE柱状图,见图4。图4(a)为不含噪声时,“十字形”的RMSE柱状图,从图中可以看出,当异常血流组织位于头皮下5 mm的全局(2250个组织单元)RMSE为13.07%,局部(10个组织单元)RMSE为23.59%;7 mm深度时,全局RMSE为13.81%,局部RMSE为35.83%。随着深度的增加,全局误差基本保持不变,但是局部误差急剧增加,深度为11 mm时,局部误差达到54.67%。全局误差小,局部误差大的原因在于Tikhonov算法之前的投影计算将整体均匀化了,被均匀化后,局部异常血流值明显下降,导致局部误差较大,而本次仿真中局部(10个组织单元)体积相比全部体积(2250个组织单元)很小,对整体影响不大,因此整体误差较小。与投影计算相反,Tikhonov正则化可以有效地保持边缘,最终使异常组织的血流得以恢复。

图4 异常组织深度增加,重建图像的RMSE柱状图
图4(b)为含噪声时,“十字形”的RMSE 柱状图,从图中可以看出,当异常血流组织位于头皮下5 mm的全局(2250个组织单元)RMSE为20.90%,局部(10个组织单元)RMSE为44.56%,远高于不含噪声时的误差值。图中全局误差依然基本保持不变,分析原因如下:
(1)在Tikhonov正则化之前,采用反投影的方法作为初值进行正则化,相当于对异常血流值进行了平滑作用,使异常血流值降低,造成了局部误差大。
(2)在本文的设置中,S-D数量(252)与体素个数(2250)的比率较小,甚至因为距离太远,某些S-D之间探测到的光子数很少,甚至没有光子被探测到,这个比率更小,导致光场自相关函数g1(τ)信号较弱,因此,重建图像的RMSE值偏高。
(3)对g1(τ)信号添加了一定的噪声,尤其是S-D距离较大时,自相关函数g1(τ)信号较弱,而噪声数据大,对重建结果影响很大。
需要指出的是:44.56%是异常血流的误差,而全局血流的误差为20.90%;因为异常血流与周围均匀组织的对比度较大,因此,这些误差的具体数值不影响本文的结论,即我们提出的Tikhonov正则化图像重建方法可以检测出异常的血流。
另外,“双条形”异常血流组织(深度5 mm)的全局(2250个组织单元)RMSE为9.19%,局部(4个组织单元)RMSE为37.87%。全局的RMSE在深度增加时依然基本维持不变,而且比“十字形”的全局RMSE小,原因是它的异常组织个数更少,只有4个。
3 结论
本文基于NL算法,并结合Tikhonov正则化算法提出了一种新颖的血流重建方法(Tikhonov-DCT)。根据这个方法,利用MC仿真得到的光子传输信息,被测组织的几何形态和内部特征等信息得以体现,同时该方法也能够充分利用测得的光学信号(即自相关曲线)。同时,Tikhonov正则化可以提高血流异质物的重建精确性和稳定性。
在采用Tikhonov正则化方法进行血流重建的过程中,发现正则化参数λ对重建效果影响很大,因此,在测试了一系列λ值以后,选定L-曲线的拐点作为λ0值,并采用迭代的方法,逐步减小λ值,以增加重建血流值的保真度。在今后的研究中将对正则化参数λ进行进一步优化,例如,使用自适应的方法来优化参数λ的数值,从而改善血流重建的质量
从重建效果可以看出,异常组织的定位较为准确,形状边缘保持较好,可以有效地区分异常组织与正常组织。与原始模型相比,Tikhonov-DCT重建图像的局部RMSE比较大,随着深度增加,急剧上升。全局RMSE较小,且随着深度增加保持微量增加。今后的工作将引入压缩感知思想优化S-D的位置和数量,增加图像重建的准确性,降低RMSE值,这些算法也将在仿体中进行实验验证。

