高密实度模拟月壤力学特性试验研究

黄 晗，吴宝广，许述财※，邹 猛，李建桥，张金换



高密实度模拟月壤力学特性试验研究

黄 晗1，吴宝广2，许述财1※，邹 猛2，李建桥2，张金换1

（1. 清华大学汽车安全与节能国家重点实验室，北京 100084； 2. 吉林大学工程仿生教育部重点实验室，长春 130022）

为保证月面采样任务顺利实施，该文以钻取采样的JLU5系列模拟月壤（JLU5-1、JLU5-2和JLU5-3，探月工程内场试验采用）为对象，利用振实装置进行高密实度模拟月壤整备，开展不同密实度条件下（相对密度为0.85、0.9、0.95和0.99）模拟月壤剪切和贯入特性力学试验，分析了相对密度对剪切强度、内聚力、内摩擦角、圆锥指数和圆锥指数梯度的影响规律。试验结果表明，剪切强度和内聚力随相对密度增加总体呈现增加规律，平均变化率分别为11.1%和35.8%；3种模拟月壤内摩擦角随相对密度增加无明显变化趋势，范围为53.3º～67.7º；圆锥指数和圆锥指数梯度随相对密度增加而增加，且圆锥指数和圆锥指数梯度平均变化率较剪切强度和内聚力的大；相同试验条件下，颗粒较细的JLU5-3型模拟月壤较JLU5-1和JLU5-2具有更大的剪切强度、内聚力和圆锥指数，JLU5-2内摩擦角总体上较JLU5-1和JLU5-3的小。利用EDEM软件建立贯入特性试验数值模型，仿真结果表明：不同模拟月壤圆锥指数仿真值总体小于实际试验值，且随相对密度变化规律一致，建立了仿真与试验值线性关系。研究结果可为采样任务顺利实施、钻取机构优化设计、采样触月部件与月壤相互作用力学模型建立提供参考。

土壤力学；力学特性；剪切强度；内聚力；内摩擦角；模拟月壤

0 引 言

自2004年正式开展探月工程以来，中国已先后完成了对月球的“绕”、“落”探测任务。目前正在实施的探月三期工程—无人自主采样任务包括表层和深层月壤采样[1-3]。表层采样使用挖取和铲取方式[4]，而深层月壤采样将利用钻取的方式获取深度约为2 m的连续月壤样品[1]。钻取采样过程中不仅取决于采样装置设计，还与月壤力学特性紧密相关。月壤的力学特性由其物理特性决定，包括颗粒形态、粒径分布、颗粒比重、相对密度等。其中，月壤的相对密度直接影响月壤的力学特性，进而影响采样装置受力及钻取效果[5,6]。由于深层月壤性质极其复杂，为确保月球探测器在月面钻取采样的顺利进行，开展面向钻取月壤力学特性试验研究具有重要意义。

由于真实月壤极其珍贵稀少，为满足地面钻取试验需求，与真实月壤具有相似矿物成分和力学特性的模拟月壤不断地被研制出来[7-9]，如JSC-1A[10-11]、BP-1[12]、CAS-1[13]、TJ-1[14]和TYII[15]等。月壤/模拟月壤的力学特性一直都是国内外相关学者的研究重点[16]。Arslan等对模拟月壤JSC-1A进行承压和剪切特性试验，将其剪切强度、抗拉强度、剪胀角等力学特性参数与真实月壤进行了对比[17]。Suescun-Florez等对BP-1模拟月壤力学特性进行测试，包括粒径分布、相对密度、压缩系数、剪切强度等[12]。张宇等对CAS-1模拟月壤开展动力学参数的试验研究，分析了不同孔隙比、不同围压对动剪切模量及剪应变的影响规律[13]。蒋明镜等对TJ-1模拟月壤承载特性物理模型试验研究，探讨了极限承载力和变形模量随加载速率变化规律[18]。

以上研究均偏向低、中密实度表层月壤力学特性研究，根据以往的探月结果，月壤的体密度随着深度的增加而增大，次表层的月壤与表层月壤相比更为密实，而与面向钻取采样的次表层高密实度月壤相关的力学特性方面的研究涉及较少。因此，采样器能否顺利完成钻取任务，其关键在于能否在高密实度的模拟月壤状态下稳定工作，因此有必要开展模拟月壤在不同密实度状态下力学特性研究。

本文采用吉林大学工程仿生教育部重点实验室研制的JLU5型模拟月壤（已被航天部门用于钻取采样地面试验研究），代替真实月壤开展相关的物理力学特性试验研究，包括承载特性和剪切特性。由于高密实度条件下模拟月壤硬度较大，压板承载试验无法达到有效贯入深度，本文采用圆锥贯入阻力特性试验代替压板承载试验。为模拟极限状态下钻取采样试验，本文研制了高密实度模拟月壤整备和测试装置，开展不同相对密度模拟月壤整备方法研究；探讨相对密度对剪切强度、内聚力、内摩擦角、圆锥指数和圆锥指数梯度影响规律；并通过EDEM软件开展贯入特性仿真对比分析，以期为采样任务顺利实施、钻取机构优化设计、采样触月部件与月壤相互作用力学模型建立提供参考。

1 材料与方法

1.1 试验设备

为实现高密实度模拟月壤整备，研制了振动压实装置，如图1所示，主要由电机、土样盒、凸轮组件等组成。电机额定转速为3 000 r/min, 额定功率为750 W，为保护设备避免温升过高，装置可允许连续工作的最长时间为10 h。通过步进电机带动凸轮组件的运动，进而使土样盒上下振动，实现模拟月壤的密实整备，电机振动频率为200次/min。为完成模拟月壤剪切特性测试，土样盒设计为上、下2部分，整备过程中，上、下土样盒采用螺栓固定，土样盒内部直径为110 mm，高度为140 mm。

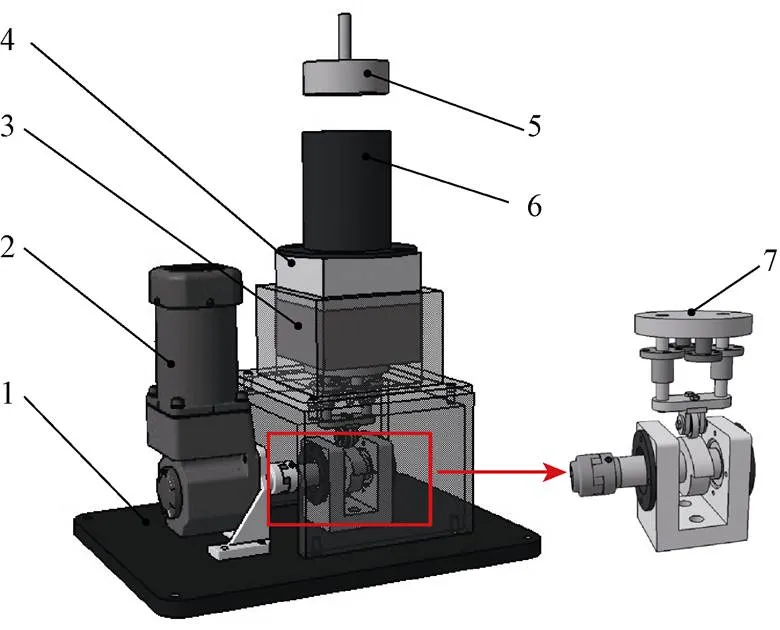
1. 支撑底座 2. 电机 3. 上土样盒 4. 下土样盒 5. 密封盖 6. 进料桶7. 凸轮组件

针对高密实度模拟月壤，研制了剪切特性试验装置，如图2所示。其中，上、下土样盒安置于压杆正下方。采用伺服电机实现恒定法向载荷加载，水平方向上通过电机推动下土样盒，与上土样盒产生相对位移，力和位移传感器分别测量剪切力和剪切位移。标准剪切速度为2.4 mm/min，剪切力测量范围为0～2 kN，最大剪切位移为9 mm。

土壤贯入阻力（又称坚实度、挤压阻力、土壤硬度）作为土壤重要的物理特性指标之一，是指土壤对外物垂直穿透时的阻力[19]。贯入阻力与圆锥基底面积的比值，这个比值称为“圆锥指数”（cone index），是判断钻取采样任务是否能顺利完成的重要参考指标之一。由于普通手持式土壤硬度仪无法满足本研究试验需求，本文研制了一种高密实度模拟月壤贯入阻力测量装置，如图3所示，主要由贯入锥头、升降机、丝杆副和数据采集PC等组成。

1. 下土样盒 2. 位移传感器 3. 上土样盒 4. 压杆 5. 力传感器

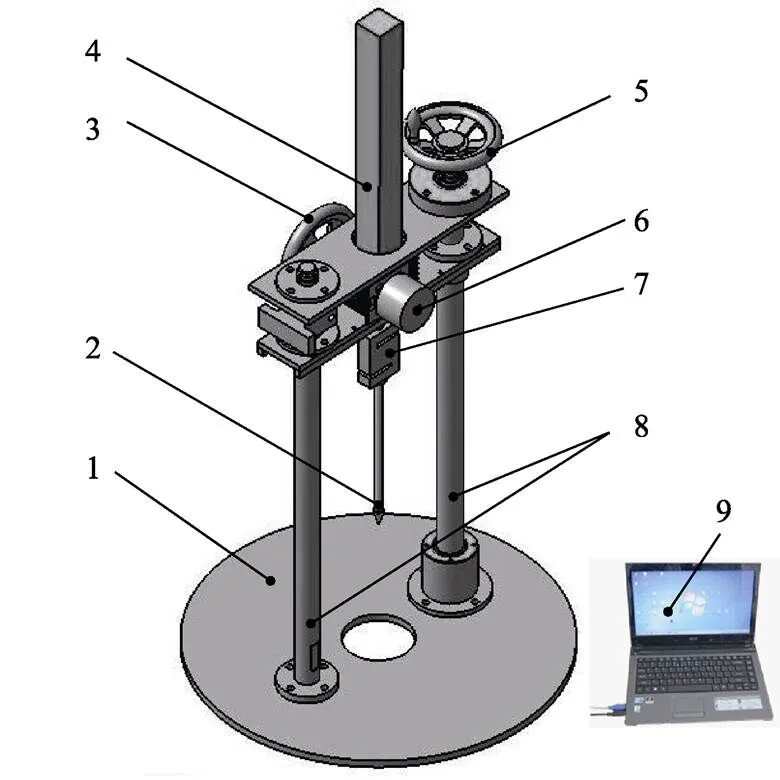
1. 支撑底板 2. 锥头 3. 副手轮 4. 升降机 5. 主手轮 6. 位移编码器 7. 压力传感器 8. 丝杠副 9. 数据采集PC

试验中，通过转动副手轮使得锥头缓慢贯入模拟月壤中，平均贯入速度约为30 mm/min，主手轮用于快速调节升降机高度。贯入阻力和深度数据分别通过压力传感器和位移编码器进行采集，其中位移传感器的精度为 0.01 mm，力传感器精度为0.01 N，数据最终由PC记录保存。贯入锥头采用淬火工艺处理，以满足高强度的试验要求，锥头的额定载荷为2 kN，最大贯入深度为100 mm。

1.2 模拟月壤及整备

本文采用的试验介质为JLU5型模拟月壤（探月工程三期内场试验采用），以吉林辉南玄武质火山灰为主要原料，通过筛选、研磨、粒径级配加工而成[19-21]，含水率小于0.3%，属于干性砂土。模拟月壤颗粒形态以棱角状和次棱角状为主，按不同粒径级配分为3种类型，如图4所示，分别为JLU5-1、JLU5-2和JLU5-3。由图4可知，JLU5型模拟月壤粒径分布均在真实月壤范围之内[22]，其中，相较于JLU5-1和JLU5-2型模拟月壤，JLU5-3的颗粒粒径偏细，接近真实月壤粒径级配上限。

注：JLU5-1、JLU5-2和JLU5-3分别代表JLU5-1型模拟月壤、JLU5-2型模拟月壤和JLU5-3型模拟月壤。下同。

对于基于模拟月壤的各项地面试验，模拟月壤在不同密实度下呈现的物理力学性质差异将对试验结果产生影响[11]。为了提高钻取的安全系数，地面试验中应放大模拟月壤密实度的范围。为获取不同密实度状态的模拟月壤，本文采用振动压实的方法进行模拟月壤整备，模拟月壤密实度用相对密度表示，如式（1）所示。

式中D为相对密度，无量纲；γmax为最大体密度，g/cm3；γmin为最小体密度g/cm3；γ为体密度，g/cm3。针对相对密度为0.85～1.00的采样模拟月壤，相对密度共分为4个等间距水平，分别为0.85、0.90、0.95和0.99，其中由于相对密度为1.00为理想状态，实际试验中无法达到，故相对密度最高取为0.99。

为获取不同水平的相对密度，需要确定最大、最小体密度和体密度。试验中，模拟月壤体密度随着振动次数增加而增大，当整备次数达到20万次时，模拟月壤体密度逐渐趋于一个稳定值，本文将这一稳定值作为最大体密度。模拟月壤最小体密度采用倾倒法获取。本文模拟月壤最大和最小体密度如表1所示。前期通过试验，得到模拟月壤体密度与振动次数关系，如式（2）所示。

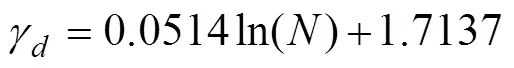
式中为振动次数。该公式计算的体密度值和实际测量值间的相对误差不超过0.2%。模拟月壤不同相对密度条件下体密度数值如表2所示。

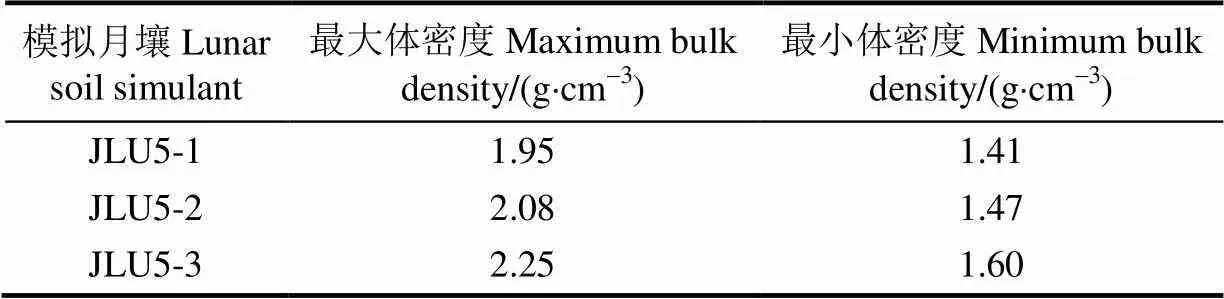
表1 模拟月壤体密度最大和最小值

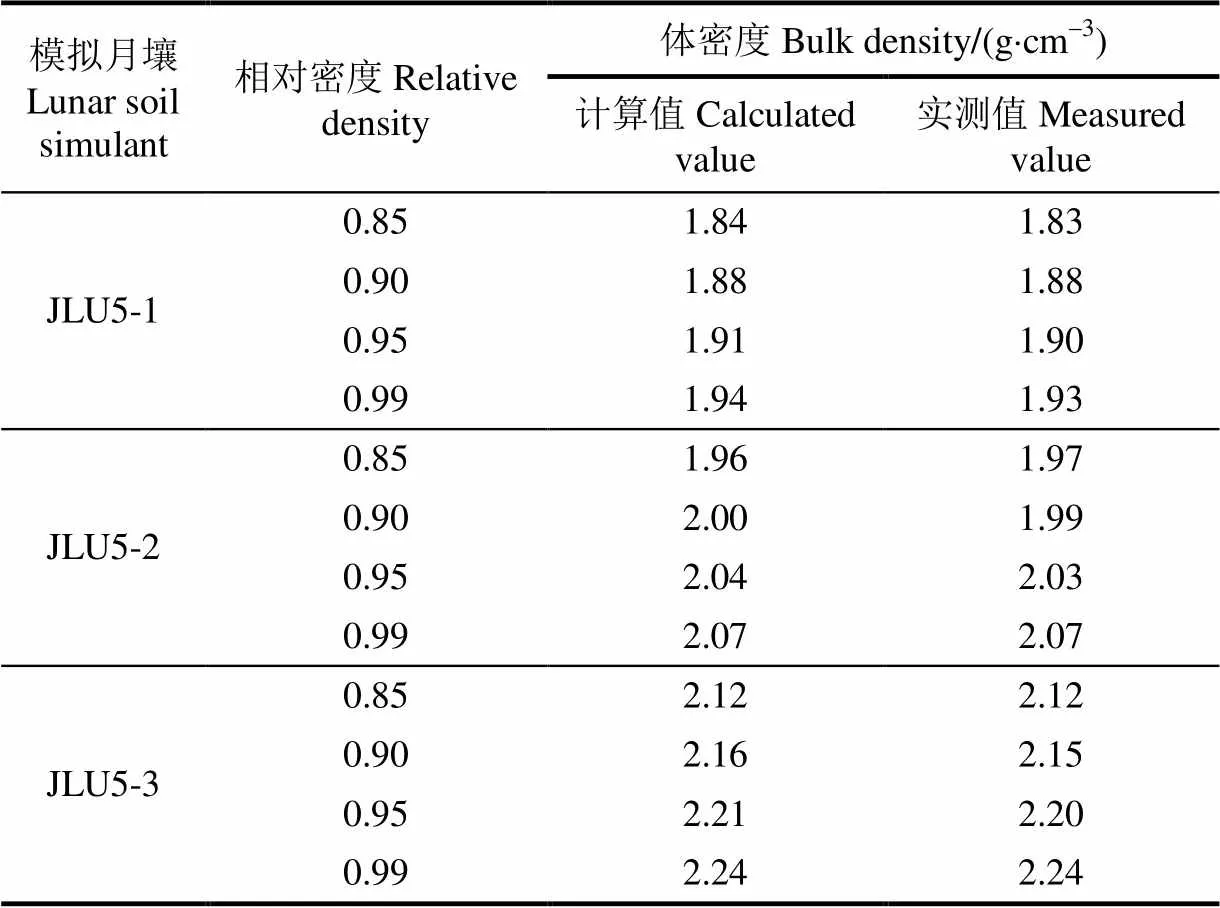
表2 模拟月壤相对密度与体密度对应关系

1.3 试验方法

在整备完成的模拟月壤基础上，开展不同密实度度条件下的贯入和剪切特性分析，获取的物理力学特征参数包括剪切强度、内聚力、内摩擦角和圆锥指数和圆锥指数梯度。

本文采用莫尔—库伦强度理论来描述月壤的剪切特性[23]，振动密实后的模拟月壤属于脆性地面，剪切特性曲线会出现最大剪切应力，即为剪切强度。通过测量不同法向应力条件下剪切强度，得到模拟月壤内聚力和内摩擦角，如式（3）所示。

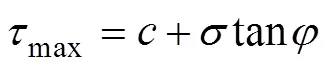
式中max为剪切强度，kPa；为内聚力，kPa；为内摩擦角，（°）；为作用在模拟月壤单位支撑面积上的法向应力，kPa。

在进行剪切特性试验时，首先将位移传感器和剪切电机调整到零位置点，并做清零处理；控制法向电机施加试验所需载荷，其数值由力传感器测量；启动水平方向电机开始剪切，根据土工试验方法标准，剪切速度设置为0.8 mm/min；当剪切位移达到9 mm时，停止试验并保存数据；最后，控制法向电机卸压，并让剪切电机后退至初始位置。试验中，法向载荷分为4个等级，分别为10、20、30和40 kPa，每级法向载荷条件下进行3次重复试验。

在进行贯入特性试验时，将整备后装有模拟月壤的土样盒放置于贯入锥头下方，并保证锥头对准土样盒中心位置。转动主手轮使锥头下降至恰好与模拟月壤表面接触，打开数据采集软件，转动副手轮使锥头贯入模拟月壤中，PC开始采集保存贯入阻力和位移数据。前期试验发现锥头下降速度对贯入阻力影响相对较小，因此，为保证锥头平均下降速度约为30 mm/min，对应副手轮转速为120 r/min），上述操作由固定试验人员完成。

2 结果与分析

2.1 剪切特性分析

模拟月壤剪切强度随相对密度和法向应力变化趋势如图5所示，3种模拟月壤剪切强度范围为36.6～158.4 kPa。相同试验条件下，JLU5-3的剪切强度最大，其次是JLU5-1，JLU5-2的剪切强度最小。模拟月壤剪切强度总体上随相对密度增加呈现增加趋势，平均变化率约为11.1%。结果表明，随着整备后模拟月壤密实度的不断增加，其抗剪能力也相应增强。

当D由0.90增加到0.95时，JLU5-1和JLU5-2剪切强度在= 20 kPa分别减少了13.5%和22.2%；当D由0.95增加到0.99时，JLU5-3型模拟月壤剪切强度在= 20、30和40 kPa呈现明显减小趋势，平均减少了16.4%。由此可见，高密实度会使模拟月壤剪切强度出现一定的波动，尤其对于颗粒较细的JLU5-3型模拟月壤。

模拟月壤不同相对密度条件下内聚力如图6所示，JLU5系列模拟月壤内聚力范围为14.9～68 kPa，约为TJ-1和JSC-1A型模拟月壤内聚力的3～10倍[14-16]。由图6可知，内聚力随相对密度增加呈现增加趋势，3种模拟月壤分别增加了24.7%（JLU5-1）、22.8%（JLU5-2）和37.5%（JLU5-3）。随相对密度增加，内聚力平均变化率为35.8%，高于剪切强度平均变化率（11.1%）。因此，相对密度对内聚力影响更为明显。

注：Dr为相对密度。下同。

图6 模拟月壤不同相对密度下的内聚力

当相对密度达到0.9时，JLU5-3内聚力较JLU5-1和JLU5-2的大，且随着相对密度逐渐增加，差距越来越明显，分析其原因是由于随着粒径变细，模拟月壤表面能作用愈加凸显，黏性效应也越显著，导致JLU5-3内聚力较大。

模拟月壤不同相对密度条件下内摩擦角如表3所示，由表3可知，内摩擦角变化范围为53.3º～67.7º，明显高于其他类型模拟月壤自然状态下内摩擦角[24-26]。模拟月壤内摩擦角随密实度增加无明显变化规律。不同相对密度条件下，JLU5-2内摩擦角总体上较JLU5-1和JLU5-3的小。

2.2 贯入特性及仿真分析

贯入特性试验中，贯入深度为40 mm。模拟月壤圆锥指数随贯入深度变化规律如图7所示，由图7可见，随着贯入深度增加，圆锥指数虽出现一定波动，但总体仍呈现增加趋势。

表3 模拟月壤不同相对密度下的内摩擦角

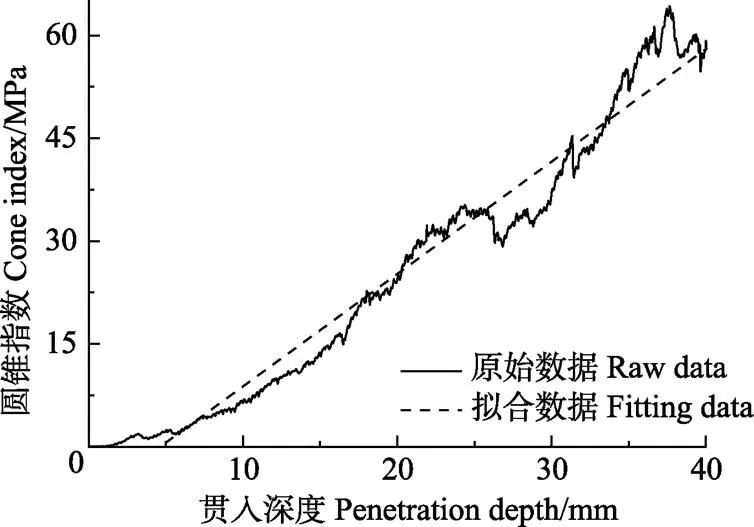
图7 圆锥指数随贯入深度的变化

图8给出了模拟月壤不同相对密度条件下圆锥指数变化趋势，由图8可知，圆锥指数随相对密度增加而增加。当贯入深度为40 mm、D为0.99时，模拟月壤圆锥指数分别达到129.8（JLU5-1）、142.9（JLU5-2）和175.2 MPa（JLU5-3）。相同试验条件下，由于颗粒较细导致模拟月壤圆锥指数增加，与内聚力随相对密度变化规律一致。相同试验条件下，JLU5-3圆锥指数较JLU5-2的增加了13.4%，JLU5-2圆锥指数较JLU5-1的增加了20.5%。结果表明，颗粒较细的模拟月壤经振动压实后圆锥指数偏大。

为对比不同密实度条件下圆锥指数，采用线性拟合方法表征其变化趋势，其斜率为圆锥指数梯度（cone index gradient）。

图8 模拟月壤不同相对密度下圆锥指数随贯入深度变化

表4为不同相对密度条件下圆锥指数梯度。当相对密度由0.85增加到0.90时，圆锥指数梯度增加较大；当相对密度由0.90增加大0.95时，圆锥指数增加不明显，进一步增加到0.99时，圆锥指数梯度则再次出现大幅度增加。随着相对密度增加，圆锥指数梯度平均增加率为50.6%，结果表明，高密实度条件下，圆锥指数梯度对相对密度增加较为敏感。

表4 不同相对密度下的圆锥指数梯度

对比3种模拟月壤，发现JLU5-3圆锥指数梯度始终较JLU5-1和JLU5-2的大，分析其原因是由于颗粒粒径偏小的JLU5-3，相同相对密度条件下实际体密度较JLU5-1和JLU5-2的大，导致模拟月壤总体上偏硬，因此JLU5-3的圆锥指数梯度最大。由于振动条件下颗粒的分离现象，导致土样盒模拟月壤存在垂直方向差异，因此，有必要进一步开展贯入特性的离散元仿真分析。

摩尔-库伦模型是岩土力学分析中应用非常广泛的塑性模型，主要适用于单调载荷下颗粒状材料[27,28]。本文采用离散元仿真软件EDEM开展贯入特性仿真分析，如图9所示。仿真建模中，模拟月壤颗粒泊松比为0.3，静摩擦系数为0.5，滚动摩擦系数为0.01[29-31]，锥头下降速度为30 mm/min，如图9a所示。由图9b可知，锥头下降的过程中，模拟月壤颗粒之间相互接触并且挤压过程中，由于压力的偏心作用，使得颗粒间发生相对滑移，圆锥指数产生一定的波动，随着贯入深度增加，圆锥指数总体上仍呈现线性增加趋势。

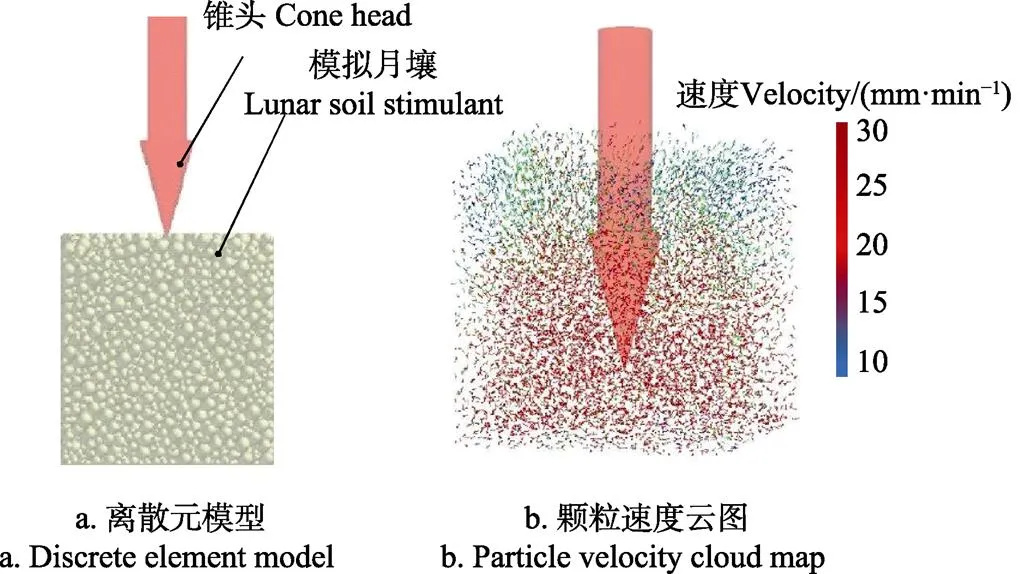
图9 模拟月壤贯入特性仿真分析

贯入特性仿真与试验结果对比如图10所示。由图10a可知，仿真结果中，圆锥指数随着贯入深度的增加而增大，且模拟月壤JLU5-3的圆锥指数较JLU5-2的大，JLU5-1的最小，与试验结果一致。

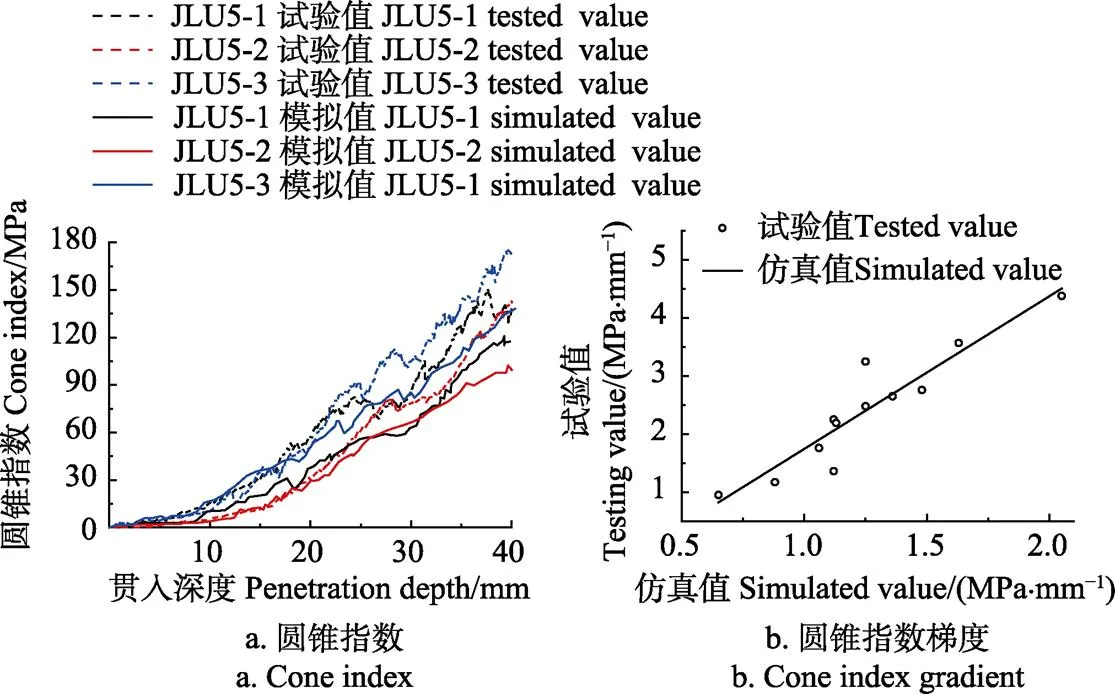
图10 模拟月壤贯入特性仿真与试验结果对比

当贯入深度大于20 mm时，随着贯入深度进一步增加，仿真值逐渐小于试验值，分析其原因可能是粒径分布与实际情况存在差异，主要是限于仿真计算速度条件，仿真中对小粒径（<0.1 mm）颗粒设置存在限制。另外，与实际试验条件相比，仿真中条件设置较为理想，模拟月壤离散程度较小，导致圆锥指数仿真值随贯入深度变化的波动较小，且线性规律较试验值更为明显。

图10b为圆锥指数梯度仿真结果与试验结果对比，由图10b可知圆锥指数梯度仿真值始终小于试验值，且与试验值存在线性关系。

3 结 论

1）提出了高密实度模拟月壤整备方法，得到模拟月壤不同体密度与振动次数关系，体密度计算值和测量值间的相对误差不超过0.2%，符合试验要求。

2）本文试验条件下，模拟月壤剪切强度总体上随相对密度增加呈现增加趋势，平均变化率约为11.1%；内聚力总体随相对密度增加呈现增加趋势，颗粒较细的模拟月壤JLU5-3内聚力较JLU5-1和JLU5-2的大；模拟月壤内摩擦角变化范围为53.3º～67.7º，且随密实度增加无明显变化规律，JLU5-2内摩擦角总体上较JLU5-1和JLU5-3的小。

3）随着贯入深度增加，圆锥指数虽出现一定波动，但总体仍呈现增加趋势；JLU5-3型模拟月壤圆锥指数较JLU5-1和JLU5-2的大，与内聚力随相对密度变化规律一致；圆锥指数梯度随贯入深度增加，平均增加率为50.6%。高密实度条件下，圆锥指数梯度对相对密度增加较为 敏感。

4）圆锥指数仿真值随贯入深度变化的波动较小，且呈现的线性规律较试验值更为明显；圆锥指数梯度仿真值始终小于试验值，建立了仿真与试验值间线性关系。

[1] 唐钧跃，邓宗全，陈崇斌，等. 面向深空探测的星球钻取采样技术综述[J]. 宇航学报，2017，38(6)：555－565. Tang Junyue, Deng Zongquan, Chen Chongbin, et al. Review of planetary drilling & coring technologies oriented towards deep space exploration[J]. Journal of Astronautics, 2017, 38(6): 555－565. (in Chinese with English abstract)

[2] 叶培建，彭兢. 深空探测与我国深空探测展望[J]. 中国工程科学，2006，8(10)：13－18.Ye Peijian, Peng Jing. Deep space exploration and its prospect in China[J]. Engineering Science, 2006, 8(10): 13－18. (in Chinese with English abstract)

[3] 吴伟仁，于登云. 深空探测发展与未来关键技术[J]. 深空探测学报，2014，1(1)：5－17. Wu Weiren, Yu Dengyun. Development of deep space exploration and its future key technologies[J]. Journal of Deep Space Exploration, 2014, 1(1): 5－17. (in Chinese with English abstract)

[4] 蒋明镜，奚邦禄，申志福，等. 月壤水平开挖推剪阻力影响因素离散元数值分析[J]. 岩土力学，2016，37(1)：229－236. Jiang Mingjing, Xi Banglu, Shen Zhifu, et al. Discrete element numerical analysis of factors affecting horizontal pushing resistance in lunar ground excavation [J]. Rock and Soil Mechanics, 2016, 37(1): 229－236. (in Chinese with English abstract)

[5] Gao Y, Thomas E D, Pitcher C. Piercing the extraterrestrial surface: integrated robotic drill for planetary exploration[J]. IEEE Robotics & Automation Magazine, 2015, 22(1): 45－53.

[6] Tian Ye, Tang Dewei, Deng Zongquan, et al. Drilling power consumption and soil conveying volume performances of lunar sampling auger[J]. Chinese Journal of Mechanical Engineering, 2015, 28(3): 451－459.

[7] 史晓萌，节德刚，全齐全，等. 模拟月壤钻进负载分析与试验研究[J]. 宇航学报，2015，35(6)：648－656. Shi Xiaomeng, Jie Degang, Quan Qiquan, et al. Experimental research on lunar soil simulant drilling load analysis[J]. Journal of Astronautics, 2015, 35(6): 648－656. (in Chinese with English abstract)

[8] Taylor L A, Pieters C M, Britt D. Evaluations of lunar regolith simulants[J]. Planetary and Space Science, 2016, 126(7): 1－7.

[9] He Chunmei, Zeng Xiangwu, Wilkinson A. Geotechnical properties of GRC-3 lunar simulant[J]. Journal of Aerospace Engineering, 2011, 26(3): 528－534.

[10] King R H, Van Susante P, Gefreh M A. Analytical models and laboratory measurements of the soil–tool interaction force to push a narrow tool through JSC-1A lunar simulant and Ottawa sand at different cutting depths[J]. Journal of Terramechanics, 2011, 48(1): 85－95.

[11] Allan S, Braunstein J, Baranova I, et al. Computational modeling and experimental microwave processing of JSC-1A lunar simulant[J]. Journal of Aerospace Engineering, 2012, 26(1): 143－151.

[12] Suescun Florez E, Roslyakov S, Iskander M, et al. Geotechnical properties of BP-1 lunar regolith simulant[J]. Journal of Aerospace Engineering, 2014, 28(5): 04014124.

[13] 张宇，余飞，陈善雄，等. CAS-1 模拟月壤动剪切模量与阻尼比的试验研究[J]. 岩土力学，2014，35(1)：74－82.Zhang Yu, Yu Fei, Chen Shanxiong, et al. Experimental study of dynamic shear modulus and damping ratio of CAS- -1 lunar soil simulant [J]. Rock and Soil Mechanics, 2014, 35(1): 74－82. (in Chinese with English abstract)

[14] Jiang Mingjing, Li Liqing, Yang Qijun. Experimental investigation on deformation behavior of TJ-1 lunar soil simulant subjected to principal stress rotation[J]. Advances in Space Research, 2013, 52(1): 136－146.

[15] Zou Meng, Fan Shichao, Shi Ruiyang, et al. Effect of gravity on the mechanical properties of lunar regolith tested using a low gravity simulation device[J]. Journal of Terramechanics, 2015, 60(4): 11－22.

[16] Sture S. A review of geotechnical properties of lunar regolith simulants[M]//Houston: American Society of Civil Engineers. 2006.

[17] Arslan H, Batiste S, Sture S. Engineering properties of lunar soil simulant JSC-1A[J]. Journal of Aerospace Engineering, 2009, 23(1): 70－83.

[18] 蒋明镜，奚邦禄，孙德安，等. TJ-1 模拟月壤承载特性物理模型试验研究[J]. 同济大学学报：自然科学版，2016，44(2)：167－172. Jiang Mingjing, Xi Banglu, Sun Dean, et al. Experimental study of bearing behavior of TJ-1 lunar soil simulant using physical model[J]. Journal of Tongji University: Natural science 2016, 44(2): 167－172. (in Chinese with English abstract)

[19] 邹猛，李建桥，李因武，等. 刚性轮—月壤相互作用预测模型及试验研究[J]. 农业工程学报，2007，23(12)：119－123. Zou Meng, Li Jianqiao, Li Yinwu, et al. Prediction model and experimental study on the interaction of rigid-wheel and lunar soil[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(12): 119－123. (in Chinese with English abstract)

[20] 黄晗，李建桥，陈百超，等. 滑转条件下星球车坡面通过性评估试验[J]. 农业工程学报，2016，32(16)：40－44. Huang Han, Li Jianqiao, Chen Baichao, et al. Experiment of slope trafficability assessment of planetary rover under slip condition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(16): 40－44. (in Chinese with English abstract)

[21] 黄晗，李建桥，吴宝广，等. 轻载荷条件下轻型车辆车轮牵引通过性模型的建立与验证[J]. 农业工程学报，2015，31(12)：64－70. Huang Han, Li Jianqiao, Wu Baoguang, et al. Research on lightweight vehicle wheel tractive trafficability model under light load[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(12): 64－70. (in Chinese with English abstract)

[22] Morris R V. Handbook of lunar soils[M]. Houston: Northrop Services, Inc., 1983.

[23] 林呈祥，凌道盛，钟世英. 模拟月壤抗剪强度试验研究及离散元分析[J]. 岩土力学，2017，38(3)：893－901.Lin Chengxiang, Ling Daosheng, Zhong Shiying. Experimental research and discrete element analysis of shear strength of lunar soil simulants[J]. Rock and Soil Mechanics, 2017, 38(3): 893－901. (in Chinese with English abstract)

[24] Klosky J L, Sture S, Ko H Y, et al. Geotechnical Behavior of JSC-1 lunar soil simulant[J]. Journal of Aerospace Engineering, 2000, 13(4): 133－138.

[25] Zeng X W, Chun M H, Heather O. Geotechnical properties of JSC-1A lunar soil simulant[J]. Journal of Aerospace Engineering, 2010, 23(2): 111－116.

[26] Perkins S W. Bearing capacity of highly frictional material[J]. Geotechnical Testing Journal, 1991, 18(4): 450－462.

[27] 张锐，罗刚，薛书亮，等. 沙地刚性轮构型仿生设计及牵引性能数值分析[J]. 农业工程学报，2015，31(3)：122－128. Zhang Rui, Luo Gang, Xue Shuliang, et al. Bionic design of configuration of rigid wheel moving on sand and numerical analysis on its traction performance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(3): 122－128. (in Chinese with English abstract)

[28] 林呈祥，钟世英，凌道盛. 模拟月壤颗粒形状特征及其对抗剪强度影响分析[J]. 东北大学学报：自然科学版，2016，37(11)：1640－1644.Lin Chengxiang, Zhong Shiying, Ling Daosheng. Analysis of particle shape characteristics of lunar soil simulant and its effect on shear strength[J]. Journal of Northeastern University: Natural Science, 2016, 37(11): 1640－1644.(in Chinese with English abstract)

[29] 林呈祥，凌道盛，钟世英. 模拟月壤抗剪强度试验研究及离散元分析[J]. 岩土力学，2017，38(3)：893－901.Lin Chengxiang, Ling Daosheng, Zhong Shiying. Experimental research and discrete element analysis of shear strength of lunar soil simulants[J]. Rock and Soil Mechanics, 2017, 38(3): 893－901. (in Chinese with English abstract)

[30] Knuth M A, Johnson J B, Hopkins M A, et al. Discrete element modeling of a Mars Exploration Rover wheel in granular material[J]. Journal of Terramechanics, 2012, 49(1): 27－36.

[31] Johnson J B, Kulchitsky A V, Duvoy P, et al. Discrete element method simulations of Mars Exploration Rover wheel performance[J]. Journal of Terramechanics, 2015, 62(6): 31－40.

[32] Jiang Mingjing, Yin Zhenyu, Shen Zhifu. Shear band formation in lunar regolith by discrete element analyses[J]. Granular Matter, 2016, 18(2): 32.

Test study on mechanical properties of lunar soil simulant under high compactness condition

Huang Han1, Wu Baoguang2, Xu Shucai1※, Zou Meng2, Li Jianqiao2, Zhang Jinhuan1

(1.100084,; 2.130022,)

In order to analyze the mechanical properties of lunar soil simulant at different densities，3 types of high density lunar soil simulant (JLU5-1, JLU5-2 and JLU5-3, which has been adopted in the Chinese lunar exploration program) was prepared by a self-designed vibrating device, the shearing and penetrating tests of 4 different soil relative density (0.85, 0.9, 0.95 and 0.99) were performed, the influence of relative density on shear strength, cohesion, internal friction angle, cone index and cone index gradient were analyzed. The result showed that the shear strength of 3 lunar soil simulant ranged from 36.6 to 158.4 kPa. The shear strength increased with the increase of relative density, the average change rate was 11.1%, which indicated that the shear capacity was enhanced with the increase of soil relative density. JLU5-3 had the largest shear strength, while the shear strength of JLU5-2 was smallest. The cohesion ranged from 14.9 to 68.0 kPa, which was about 3 to 10 times higher than that of lunar soil simulant JSC-1A and TJ-1. The cohesion increased by 35.8% with the increase of relative density, the average change rate for different lunar soil simulant was 24.7% (JLU5-1), 22.8% (JLU5-2) and 37.5% (JLU5-3), respectively. When the relative density reached 0.9, the cohesion of JLU5-3 was larger than that of JLU5-1 and JLU5-2, and the difference between them increased apparently, which may due to the effect of interface energy and viscidity became more obvious with the decreasing of soil grain size. The internal friction angle ranged from 53.3º to 67.7º, which had no obvious variation trend with the increase of relative density. The internal friction angle of JLU5-2 was always smaller than that of the JLU5-1 and JLU5-3 under different soil relative density conditions. The internal friction angle of JLU5 under high compactness condition was apparently larger than other series lunar soil simulant regolith under natural condition. When penetration depth reached 40 mm in the tests, the cone index of 3 types high-density simulant lunar soil were 129.8 MPa (JLU5-1), 142.9 MPa (JLU5-2) and 175.2 MPa (JLU5-3), respectively. Cone index presented the fluctuations but generally increased with the increase of penetration depth, smaller grain size lead to the increasing of cone index under same testing condition, which was similar to variation trend of cohesion. The cone index of JLU5-3 increased by 13.4% on average compared with that of JLU5-2, and the cone index of JLU5-2 increased on average by 20.5% compared with that of JLU5-1. Cone index gradient was defined as the curve gradient of the cone index versus with penetration depth. When the relative density changed from 0.85 to 0.9 and 0.95 to 0.99, the cone index gradient obviously increased, while there was no significant increase for cone index gradient when relative density changed from 0.9 to 0.95. The average increasing ratio of cone index gradient was 50.6% with the increasing of relative density, greater than that of the cohesion, which indicated that cone index gradient was more sensitive to soil relative density. For different types of lunar soil simulant, JLU5-3 had larger shear strength, cohesion and cone index and cone index gradient than that of JLU5-1 and JLU5-2 under same testing conditions, which may due to JLU5-3 had smaller particle size. Numerical model for penetration characteristic test had been conducted by using discrete element method software (EDEM), simulation results showed that, the simulative value of cone index was always smaller than that of the testing value, however, their variation trend versus with the relative density was consistent. A linear relation model between simulative and testing value was established, the determination coefficient value of the proposed model was 0.87. The simulation method could provide technique method for cone index prediction of lunar soil simulant under high compactness condition. The results of this paper were expected to provide references for drilling sampling mission of lunar soil, optimization design of drilling mechanism, and establishment of mechanical interaction model between drilling component and lunar soil.

soil mechanics; mechanical properties; shear strength; adhesion; internal friction angle; lunar soil stimulant

2018-06-26

2018-10-10

国家自然科学基金资助项目（51375199）；中国博士后科学基金面上资助项目（2018M641338）

黄 晗，博士，主要从事地面机器系统及其仿生研究。Email：huanghan452012@163.com

许述财，博士，副研究员，主要从事汽车被动安全性方面的研究。Email：xushc@tsinghua.edu.cn

10.11975/j.issn.1002-6819.2019.01.004

TU 411

A

1002-6819(2019)-01-0031-08

黄 晗，吴宝广，许述财，邹 猛，李建桥，张金换.高密实度模拟月壤力学特性试验研究[J]. 农业工程学报，2019，35(1)：31－38. doi：10.11975/j.issn.1002-6819.2019.01.004 http://www.tcsae.org

Huang Han, Wu Baoguang, Xu Shucai, Zou Meng, Li Jianqiao, Zhang Jinhuan.Test study on mechanical properties of lunar soil simulant under high compactness condition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(1): 31－38. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.01.004 http://www.tcsae.org