TOPSIS和突变级数方法耦合在水资源脆弱性研究与应用

曹 杰

(山西省水文水资源勘测局，山西 太原 030001)

水资源脆弱性定义为：水资源系统易于遭受人类活动、自然灾害威胁和损失的状态，受损后难以恢复到初始状态和功能的性质[1]。近年来，气候变化和水资源的过度开发利用严重影响了水资源系统的替换与更新周期，对自然资源造成了一定程度上的破坏。邹君[2]等人利用GIS技术，以衡阳盆地为实例对南方丘陵区农村水资源进行了脆弱性评价；崔东文[3]运用改进的BP神经网络在云南文山州的水资源脆弱性中进行了验证；钱龙霞[4]等人运用投影寻踪的脆弱性S型函数建立模型体系，经过在泉州市的运用，证实其可行；周念清[5]等人将压力驱动模型引入脆弱性评价中，并且取得了良好的效果。但是，影响水资源脆弱性的因子很多，根据脆弱性因子的检测数据构建出的模型，比较复杂，需要结合权重进行排序，求权重时，主观因素和客观因素对定义权重的差别很大，也有将各种方法相结合，但是求解方式过于繁琐，在很大程度上影响了最后的结果。

水资源脆弱性评价，实际上是根据多个不确定性指标，选取合适的不确定性模型或者方法，为管理者提供有效依据。本文提出了将TOPSIS综合评价法引入了突变级数法中，二者的耦合，综合了两种方法的长处。TOPSIS综合评价法弥补了突变级数法在对同层的各种属性指标进行排序过程中出现的误差，是对突变级数法的改进，最后将其应用到实例中去，进行验证。

1 水资源脆弱性评价指标体系和分级标准

水资源系统指标主要从内部自然承载能力和外部压力驱动情况两个角度考虑，本文将其分成8个指标。如图1所示，其中，内部自然承载因素包含4个指标，包括人均水资源量、降水量、产水模数、径流系数[6]；外部压力驱动因素同样包含了4项指标，分别为人均GDP、万元增加值用水量、人均供用水量、灌溉率。人均水资源量衡量了某区域水资源的丰富水平，径流系数反映了某地区的产水能力，而灌溉率显示的是一种灌溉能力。

图1 水资源脆弱性评价指标体系

对水资源脆弱性的评价指标，本文将以不脆弱、较不脆弱、中等脆弱、较脆弱和非常脆弱作为分类标准[7]。等级标准值以文献[8]为基础，并结合当地的实际情况分析给出，结果见表1。但对于突变级数建立的模型，不能使用一般情况下的评价值，突变级数法运算的评价结果会偏高，需要进行重新定义，制定出符合该方法的评价体系，将原评价指标看做一种相对隶属度，那么，对于相对隶属度为W(W=0.2，0.4，0.6，0.8，1)，经过突变模型的运算，得出新的评价等级，见表2。

表1 评价指标分级标准

表2 突变级数等级

2 TOPSIS法和突变级数法耦合模型

2.1 基于TOPSIS法的相对重要程度排序

Topsis模型通常又被称为“逼近理想解排序方法”，是常见的对有多个目标层次的系统进行距离综合排序的方法，通过计算一个测量度，衡量一个需要评价的目标对象靠近正理想解和负理想解的程度[9]，从而得到样本集的排序，其与正理想解越接近，排名就越高[10]。即此时重要程度就越高。

求解步骤如下：

(1)建立待评价目标函数的原始数据矩阵。有j个待定的评价样本，每个样本含有i个评价指标，可以将每个评价样本中的所有指标的数据看成一个j×i维的空间矩阵P。

则：

(1)

(2)原始数据的归一化。对于原始数据，不能放置于同一评价标准进行比较，需要用到归一化，将所有的数据同化为一个可比较的态势，范围为0-1。评价指标也可以分为两种类型，一是对脆弱性有正影响的指标，另一类就是对脆弱性产生负影响的指标，二者的归一化是不同的。公式如下：

式(2)为第一类指标的归一化公式，表示指标数越大，对脆弱性的正影响力越大。

(2)

式(3)为第二类指标的归一化公式，表示指标数越大，对脆弱性的负影响力越大。

(3)

式中，m=1，2……j，n=1，2……i。

对于原始数据按照上述计算公式进行归一化之后，得到标准矩阵Q。

(4)

(3)计算最大和最小向量解。其中，每个评价指标都包含最大值和最小值，为了方便之后的计算，此时最大值和最小值向量解分别为：

(5)

(6)

(4)测量到正负理想解的距离。对于某个确定指标来说，将其与每个样本中所测得的数据进行比较。分别计算与每个指标与最大值和最小值的距离，来判断该指标的好坏[11]。

(7)

(8)

其中，L+，L-—与正理想解和负理想解的欧式距离，n=1，2……i[12]。

(5)排序原则。用Jn表示与最大值和最小值的相对接近程度，按照其大小进行排序，得出每个层次的指标的重要程度排行。

(9)

2.2 基于突变级数法的评价模型

突变级数法，是一种对评价目标进行多层次矛盾分解，然后利用突变理论与模糊数学相结合产生突变模糊隶属函数[13]。其运算的主要特点即是不需要计算权重，对于在此过程中所产生的人为因素误差可以避免，经过归一化公式的量化运算，逐级推导，从下层的指标层逐渐向上级计算，最后得出一个总的隶属度函数。突变级数法的关键在于突变点，即打破原稳态的一个临界点，巧妙的利用动态拓扑理论。利用状态变量和控制变量构成的势函数来使系统的状态发生变化[14]。状态变量映射在控制变量上的奇点集构成的曲面就是分叉集，用来合理形容系统的突变过程。

常见的突变类型可以分为四类，有折叠突变、尖点突变、燕尾突变和蝴蝶突变。这四种突变类型在于其所包含的子属性数量，若对应1个子指标，是折叠突变，若对应2个指标，是尖点突变，若对应3个指标，是燕尾突变，若对应4个指标，是蝴蝶突变，每种突变的不同的详细情况见表3，其中，n—控制变量，x—状态变量，二者共同构成了势函数P(x)。

将每个层次求解出来的值用两个原则进行选择，接下来才能进行下一级的运算，其一是“取均值”，适用情况是该层次中每个状态变量都是相互影响的；其二是“取最小值”，适用情况是该层次中每个状态变量都是独立的，不存在互补关系。本文所选的求解方式是取平均值。

3 实例应用

3.1 研究区域概况

某市位于河南省西部，地处黄河中游[15]。全境东西长约254km，南北宽约234km，总面积15229km2，属暖温带半干旱大陆性气候区。地形地貌较为复杂，该市水资源主要由境内地表径流、过入境地表径流、地下径流三部分组成。其特点是水资源量主要由天然降雨补给，故水资源量随降雨的年内年际变化而变化。

该市水资源总量紧缺，同时受到人类不合理开发和污染的影响，水质也日益下降，水资源脆弱性问题较为突出，影响了该市人民的正常生活，由此，需对该市的水资源脆弱性问题进行评估，从而找到解决办法。

经过实地勘测与当地数据相结合，将6个样本集的实测数据统计见表4。

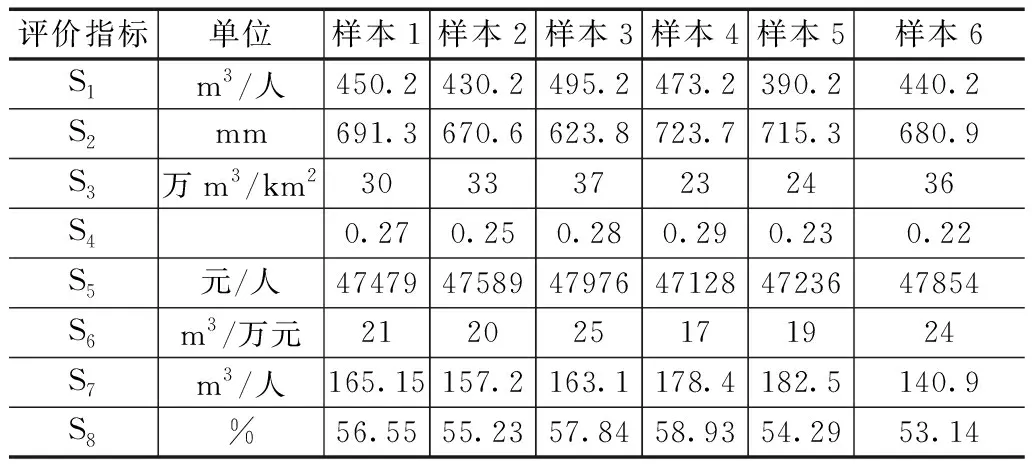
表4 6个样本的评价实测值

3.2 模型结果运算展示

由式(1)～(4)可知，对于样本所构成的矩阵和计算出来的归一矩阵如下：

表5 评价结果

最终结果得分突变类型控制层得分突变类型指标层原始值排序0.930.930.93尖点突变内部自然承载因素外部压力驱动因素0.93 0.83 0.85 0.88 0.74 0.79 0.84 0.87 蝴蝶突变蝴蝶突变产水模数/(万m3/km2)0.87 1 降水量/mm0.57 2 人均水资源量/(m3/人)0.53 3 径流系数0.52 4 人均供水量/(m3/人)0.55 1 工业万元增加值用水量/(m3/万元)0.53 2 灌溉率/%0.51 3 人均GDP/(元/人)0.49 4

由式(5)～(6)可知：

Q+=(0.18，0.18，0.20，0.19，0.17，0.20，0.18，0.18)

Q-=(0.15，0.15，0.13，0.14，0.17，0.13，0.14，0.16)

其中Qn+为0.20，Qn-为0.13。

由式(7)～(9)可知：

L+=(0.054，0.031，0.113，0.067，0.005，0.095，0.056，0.026)

L-=(0.060，0.041，0.308，0.071，0.004，0.095，0.068，0.025)

Jn=(0.526，0.573，0.731，0.516，0.494，0.500，0.547，0.496)

由此可知，对于内部因素，根据上式的计算结果可看出，指标的排序情况是产水模数，降水量，人均水资源量，最后是径流系数。对于外部因素，四个指标的顺序应为人均供水量，工业万元增加值用水量，灌溉率，排列最后的是人均GDP。对于包含4个指标的指标层，应选择蝴蝶突变来进行计算，并且根据所求出的贴合度进行了相对重要程度的排序。对于控制层来说，最好适用于包含两个状态变量的尖点突变来计算，计算结果见表5。

表4评价结果显示，结合6个样本的实测数据，最终该方法求出的结果为0.93，在中等脆弱的评价范围内，因此，该市2013年的评价结果为中等脆弱。该市水资源总体较好，但是仍然存在一系列问题，比如供给方面和水质方面，仍需加大对该地的水资源的管理与监控。

4 结论

(1)本文将TOPSIS首次引入到水资源脆弱性计算，并结合突变级数法对某市的实测数据进行评价，取得了较好的结果，与实测数据进行比较证明该种方法是合理的。

(2)突变级数法结合TOPSIS法能使得两种方法的优势凸显，前者计算简便，不需要计算各个指标的权重系数，极大的避免了主观因素和客观因素对计算结果的影响，但在相对重要程度排序上有一定的缺陷，后者正是对这个缺陷的补充，采用理想值逼近法计算每个指标在该指标层中的相对重要程度。

水资源脆弱性评价是目前研究的热点，其他更加精确的方式还有待开发。本文也有一定程度的缺陷，还需要在之后的研究中解决。