核电厂预应力混凝土安全壳结构抗震裕度评估*
薛志成,彭云志,裴 强,朱孔琛,张 瑶
(1.黑龙江科技大学 建筑工程学院,哈尔滨 150022;2.大连大学 土木工程技术研究与开发中心,辽宁 大连 116622)
核安全壳结构作为核电工程的Ⅰ类物项,是防止发生核泄漏的最后一道屏障,其地震作用下的安全性能对保证核电厂安全运行具有极其重要的作用,因此,强震作用下核安全壳结构的抗震性能及损伤评估已成为核电工程抗震领域的研究重点.增量动力分析(incremental dynamic analysis,IDA)法是将单一的时程分析扩展为增量时程分析,该方法具备了静力弹塑性分析和非线性时程分析的诸多优点[1].近年来,增量动力分析法在核电工程结构地震易损性分析方面得到了应用,Firoozabad等[2]采用等效线性模型和双线性模型模拟核安全壳隔震结构分析模型,进行核安全壳隔震结构地震易损性分析;陈健云等[3]采用增量动力分析法(IDA)和多样条分析法(MSA)进行隔震与非隔震核岛厂房的地震易损性分析,验证了隔震措施可以有效地提高核岛厂房的抗倒塌能力;Jha等[4]基于非线性静力分析法提出了一种结构抗震裕度评估方法;Kim等[5]采用MCS和LHS研究了NNP系统易损性的不确定性,通过计算HCLPF值来查验不确定性分析的收敛性,估计NNP系统的年失效概率,并与其他研究成果进行对比分析.
采用有限元分析软件ABAQUS建立核安全壳结构三维有限元分析模型,利用增量动力分析法对核安全壳结构进行地震易损性分析,研究在不同强度地震作用下核安全壳结构发生开裂破坏的概率.采用抗震裕度评估方法中的地震易损性分析法对核安全壳结构进行抗震裕度分析.
1 结构地震易损性分析原理
增量动力分析法是对结构有限元模型输入一条或多条地震动,每一条地震动均按一定比例进行调幅,计算结构在该组调幅地震动作用下的非线性动力时程响应,提取时程分析结果,得到一系列地震动强度指标IM(intensity measures)与对应的结构损伤指标DM(damage measures)的点,在DM-IM直角坐标系中将这些点拟合成一条曲线,即IDA曲线.
结构工程需求参数(EDP)与地震动强度指标(IM)之间的关系[6]为
EDP=α(IM)β
(1)

(2)
对式(2)两边取自然对数可得
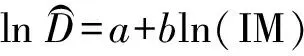
(3)
式中,a、b为常数,a=lnα,b=β.
结构地震响应的概率函数D服从对数正态分布,其统计参数为
(4)
(5)
式中:λd为D的对数平均值;βd为D的对数标准差;N为D的样本总量.
结构抗震能力参数概率函数C服从对数正态分布,也可按照式(4)、(5)来表示C的对数平均值λc和对数标准差βc.
结构特定阶段的失效概率可表示为
(6)
式中:pf为地震作用下结构超越某一性能水准的概率;Φ为标准正态分布函数.
2 核安全壳结构有限元模型建立
某预应力混凝土核安全壳结构由半球形穹顶、圆柱形筒体和基础底板三部分组成.半球形穹顶内径40 m、穹顶壁厚0.9 m;圆柱形筒体内径40 m、筒体高48 m、筒壁厚1.1 m;基础底板厚6.5 m;结构总高度68.9 m;混凝土强度等级为C50[7].核安全壳结构几何尺寸如图1所示(单位:m).
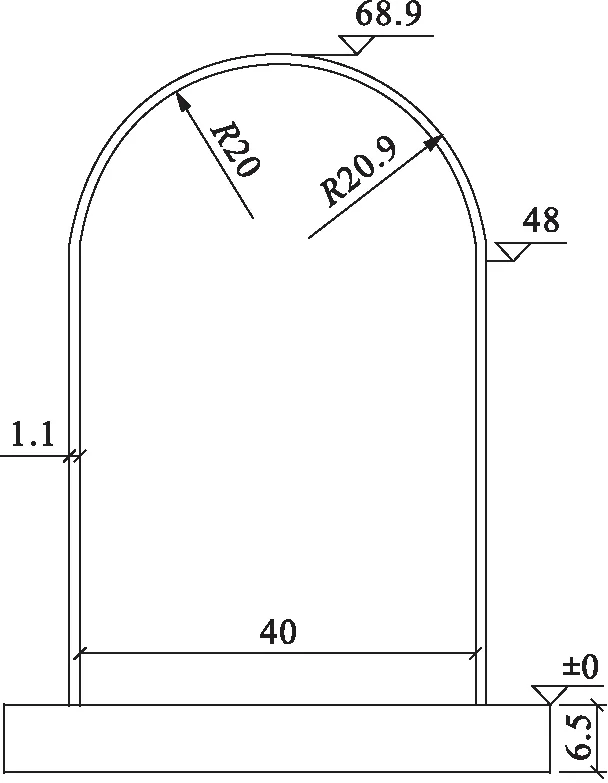
图1 核安全壳结构几何尺寸Fig.1 Geometrical dimension of nuclear containment vessel structure
在进行建模时,核安全壳结构穹顶及筒体采用C3D8R单元模拟;建模时将基础视为刚性基础,采用R3D4单元模拟;环向和竖向预应力钢筋均采用T3D2单元模拟,普通钢筋采用REBAR+SURFACE的方法模拟;采用降温法模拟预应力的施加;预应力钢筋和普通钢筋均采用ABAQUS内置的Embedded命令嵌入混凝土单元中.核安全壳结构三维有限元分析模型中共有56 831个单元、52 662个节点,核安全壳结构有限元分析模型如图2所示.
3 核安全壳结构地震易损性分析
3.1 地震动输入
核电厂场址抗震设防烈度为7度;场地类别为Ⅱ类;设计地震分组为第三组;设计基准地震强度PGA为0.20g.据此从美国太平洋地震研究中心(PEER)强震记录数据库中选择15条具有一定代表性的实际地震动记录.地震动信息如表1所示,所选地震动的反应谱如图3所示.

图2 核安全壳结构有限元分析模型Fig.2 Finite element model for nuclear containment vessel structure

表1 输入地震动记录Tab.1 Input earthquake records
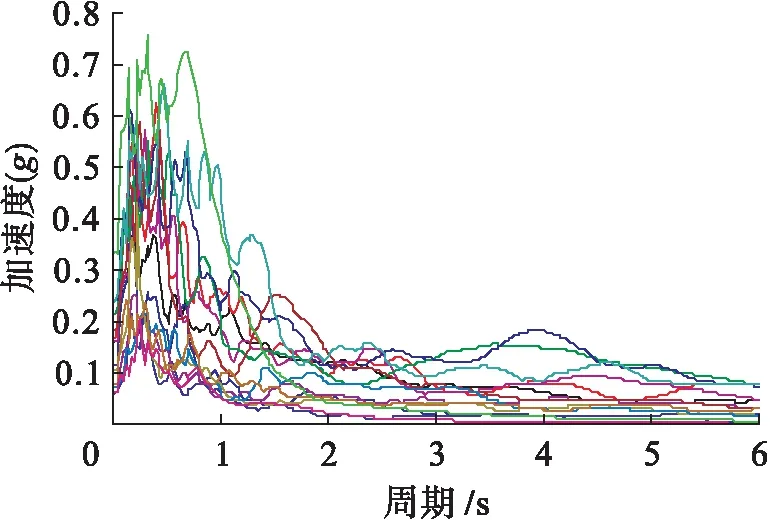
图3 地震动反应谱Fig.3 Earthquake response spectrum
为了说明IDA曲线的差异性,引入线性IDA曲线的概念,线性IDA曲线的斜率与结构处于线弹性阶段IDA曲线斜率相等[8].图4a为硬化型IDA曲线,图中结构IDA曲线位于线性IDA曲线的上方,IDA曲线表现出“震荡”现象,即随地震动强度增大结构损伤降低.对于实际结构而言,意味着结构的损伤积累发生在结构的不同部位,最终导致结构塑性耗能大大提高,抵抗地震的能力大大提高[9].图4b为软化型IDA曲线,图中结构IDA曲线位于线性IDA曲线的下方,该模式下结构IDA曲线比较平滑.图4c为过度软化型,图中结构IDA曲线表现出一定的“硬化”特征,随着结构顶点水平位移的增加,IDA曲线出现“软化”现象.
3.2 地震动强度指标及结构损伤指标
对于短周期结构,其地震响应与PGA的相关程度较高[10],核电厂结构在进行地震易损性分析时,以PGA作为地震动强度指标[11-12].对核安全壳结构进行地震易损性分析时,发现核安全壳结构顶点位移比随PGA的增加而增大,故将核安全壳结构顶点位移作为结构整体损伤指标.
为了得到核安全壳结构发生开裂时的顶点水平位移损伤指标,采用均布侧向力加载模式,对核安全壳结构进行静力弹塑性分析,分析结果如图5所示.由图5b可知,核安全壳结构发生开裂时的顶点水平位移为20.6 mm,响应的基底剪力为4.276 9×105kN.由图5c核安全壳结构发生开裂时的PEEQ云图可知,均布侧向力加载模式下结构底部率先发生开裂.
3.3 IDA曲线绘制
单一地震动按一定比例进行调幅,调幅后的PGA分别为0.2g、0.4g、0.6g、…、1.8g、2.0g,将其作为地震动输入,对结构进行10次非线性时程分析,得到10个PGA及其对应的结构顶点水平位移数据点,采用Origin软件将得到的数据点汇总在DM-IM直角坐标系中.为了得到较平滑的IDA曲线,采用样条插值的方法对坐标系中点与点之间进行插值,可得到单一地震动作用下核安全壳结构IDA曲线.整理IDA数据,得到核安全壳结构IDA曲线簇,如图6所示.

图4 三类IDA曲线Fig.4 Three IDA curves
3.4 结构地震概率需求模型建立
对核安全壳结构进行增量动力分析,得到多组PGA及其对应的结构顶点水平位移y数据,即IDA数据.以PGA的自然对数作为自变量,以结构顶点水平位移y的自然对数作为因变量,建立ln IM-ln DM直角坐标系,利用Origin软件对坐标系中数据进行线性回归分析,得到核安全壳结构地震概率需求模型,线性回归分析结果如图7所示.
核安全壳结构地震概率需求模型可表示为
lny=-3.666+0.996ln PGA
(7)
式中,a=lnα=-3.666,α=0.025 6.

图5 核安全壳结构Push-over分析结果Fig.5 Push-over analysis results of nuclear containment vessel structure
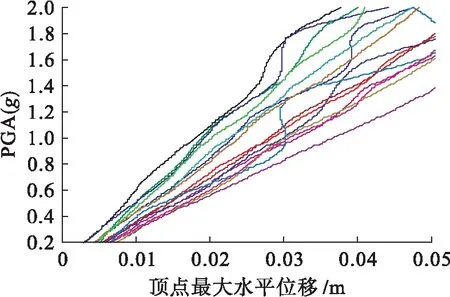
图6 核安全壳结构IDA曲线簇Fig.6 IDA curve cluster of nuclear containment vessel structure
3.5 易损性曲线绘制
根据式(6),以PGA为自变量的结构失效概率可表示为
(8)
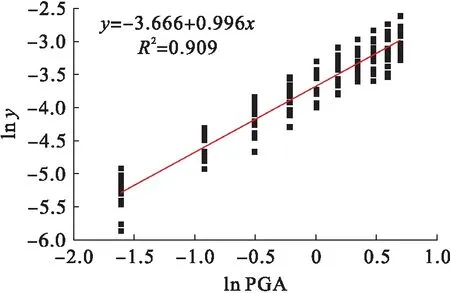
图7 核安全壳结构地震概率需求模型Fig.7 Seismic probability demand model for nuclear containment vessel structure
(9)
以PGA为横坐标,Pf为纵坐标,绘制核安全壳结构地震易损性曲线,如图8所示.
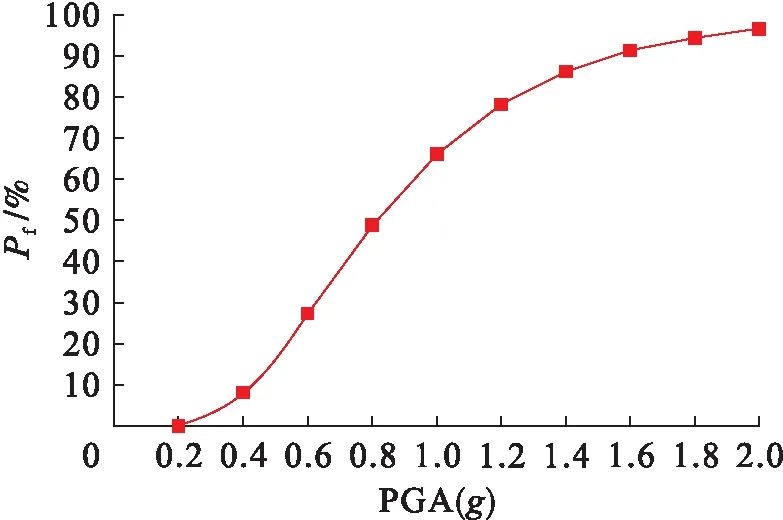
图8 核安全壳结构地震易损性曲线Fig.8 Seismic fragility curve of nuclear containment vessel structure
由图8可知,核安全壳结构地震易损性曲线大体成“S”形.随着地震动强度的增加,结构发生开裂破坏的概率逐渐增大.当PGA=0.35g时,结构发生开裂的概率约为5%;当PGA=0.42g时,结构发生开裂的概率约为10%;当PGA>0.4g时,结构发生开裂的概率增长速度明显加快,说明此阶段核安全壳结构发生开裂的概率对地震动强度的变化十分敏感.
4 核安全壳结构抗震裕度分析
采用地震易损性分析法(SFA)对核安全壳结构进行抗震裕度分析,该方法通过定义一组地震易损性曲线来表示不同置信度水平下地震动水平与结构失效概率的关系.
在特定失效模式下,结构易损性曲线组可通过中值地面加速度能力Am和随机变量eR、eU来表示.因此,地面加速度能力A[13]可表示为
A=AmeReU
(10)
假定eR、eU均服从对数正态分布,对数标准差分别为βR和βU.
只考虑随机不确定性βR时,在确定的失效模式和地面加速度能力参数下,指定PGA水平θ时,结构的条件失效概率为
(11)
式中:φ(·)为标准高斯累积分布函数;θ为地面加速度.
考虑认识不确定性βU时,易损性就成为不确定的随机变量,在任意PGA水平θ时,易损性f均可用主观概率密度函数表示,f (12) 式中:φ-1(·)为标准高斯累积分布的反函数;Q=P(f 抗震裕度评估中非常重要的一部分就是对核电厂SSC的抗震能力进行评估,其抗震能力值通常用高置信度低失效概率(HCLPF)值表示,HCLPF值是一个加速度值,当地面加速度处在这个水平上时,分析人员有95%的置信度认为核电厂SSC的失效概率小于5%.核电厂SSC的HCLPF值可表示为 (13) 式中,βC为复合的不确定性参数,βC=(βR+βU)1/2,将βC替代式(11)中的βR可得到均值易损性曲线. 依据核安全壳结构地震易损性分析数据,得到一组地面加速度能力及其对应的核安全壳结构开裂概率.根据式(11)、(12)可得具有5%、50%、95%置信度水平的核安全壳结构地震易损性曲线,并由式(13)计算结构高置信度低失效概率值. 图9给出了具有不同置信度水平的核安全壳结构地震易损性曲线组.由图9可知,随着地震动强度的增加,结构的开裂概率逐渐增加.同一强度地震动作用下,具有95%置信度水平地震易损性曲线对应的结构开裂概率最大,易损性分析结果偏保守;具有5%置信度水平地震易损性曲线对应的结构开裂概率最小,易损性分析结果偏大.核安全壳结构HCLPF值为0.254g. 图9 核安全壳结构地震易损性曲线组Fig.9 Seismic fragility curve group of nuclear containment vessel structure 本文运用有限元分析软件ABAQUS建立核安全壳结构三维有限元分析模型,采用增量动力分析法进行核安全壳结构地震易损性分析,得到核安全壳结构地震易损性曲线,并对核安全壳结构进行抗震裕度评估,结论如下: 1) 采用均布侧向力加载模式对核安全壳结构进行静力弹塑性分析,得到核安全壳结构发生开裂时的顶点水平位移损伤指标为20.60 mm. 2) 采用增量动力分析法得到以核安全壳结构顶点水平位移为横坐标,以PGA为纵坐标的IDA曲线簇.IDA曲线簇表明,IDA曲线形状受到地震动记录的影响,不同地震动记录作用下核安全壳结构的IDA曲线表现出一定的离散性.随着地震强度的增加,IDA曲线簇的离散性逐渐体现并越发明显. 3) 通过对增量动力分析数据进行线性回归分析,得到核安全壳结构地震概率需求模型,计算了核安全壳结构在不同强度地震作用下发生开裂破坏的概率. 4) 采用地震易损性分析法对核安全壳结构进行抗震裕度评估,确定其HCLPF值为0.254g,该值为安全停堆地震水平的1.27倍,说明核安全壳结构具有良好的抗震能力.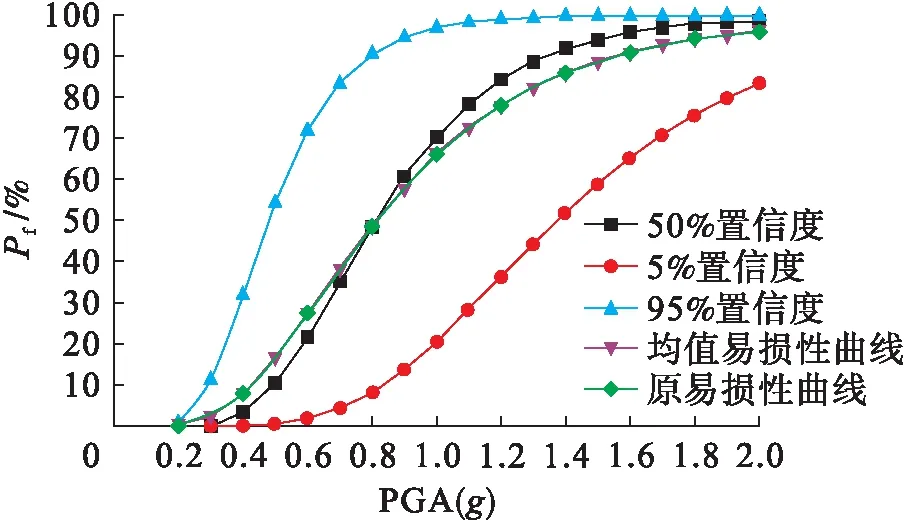
5 结 论

