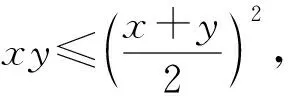优美对称的和谐表达 相等不等的自然链接
——两道全国联赛题的统解与猜想
●
(湖州市王勇强名师工作室,浙江 湖州 313000)
2017年和2018年的全国初中数学联合竞赛填空压轴题均以二元三次方程为约束条件命制,试题形式简洁,内涵丰富,颇有研究价值.
1 赛题呈现和比较
例11)若实数x,y满足x3+y3+3xy=1,则x2+y2的最小值为______.
(2017年全国初中数学联合竞赛试题第8题)

(2018年全国初中数学联合竞赛试题第8题)
两道赛题形式简洁,结构优美且神似,本质相通.赛题把不同的轮换对称式巧妙地融入条件和求解的结论之中,既很好地展示了数学的简洁美和对称美,又增强了视觉效果和可操作性.
2 赛题分析和求解
细心的读者一定会发现这两道赛题的吸引眼球之处:代数式xy,x+y,x2+y2,x3+y3都具有轮换对称性,因此它们呈现的约束条件和结论是相互关联的,解决赛题的策略也有共性.因为对称代数式xy,x+y,x2+y2,x3+y3之间可以用相等或不等相互转化,因此解题目标可以从相等和不等两个视角切入.
2.1 从相等关系入手,构造方程求解
由于轮换对称的代数式x2+y2,x3+y3均可以用基本对称式xy,x+y表示出来,即
x2+y2=(x+y)2-2xy,
x3+y3=(x+y)[(x+y)2-3xy],
因此自然地联想到韦达定理,构造一元二次方程,利用判别式大于或等于0求解.又这两道赛题结构神似,故可以通过构造一元二次方程来统一求解.解法如下:
解法11)设x+y=t,则
t(t2-3xy)+3xy=1,
即
(t-1)(t2+t+1-3xy)=0,
从而
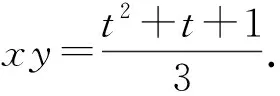
①当t=1,即x+y=1时,
x2+y2=x2+(1-x)2=2x2-2x+1=

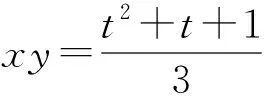
即
(t+2)2≤0,
得
t=-2,
故
x=y=-1,
此时
x2+y2=2.
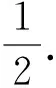
2)设x+y=t,则
即
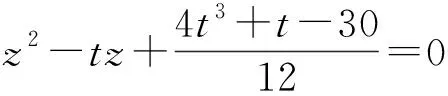

于是t>0,即
t3+t-30≤0,
进而
(t3-3t2)+(3t2+t-30)≤0,
即
(t-3)(t2+3t+10)≤0.

2.2 从不等关系入手,挖掘不等式求解

(当且仅当x=y时,取到等号).详情请参阅文献[1].
下面尝试用这条不等式“链”来求解上述两道竞赛题.
解法21)设x+y=t,则
t(t2-3xy)+3xy=1,
即
(t-1)(t2+t+1-3xy)=0,
故
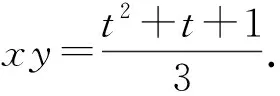



化简整理,得
(t+2)2≤0,
即
t=-2,
故
x=y=-1,
此时
x2+y2=2.
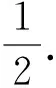
2)设x+y=t,则
即
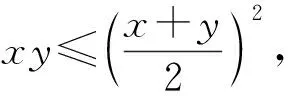
(1)

从而
t>0.
化简式(1),整理得t3+t-30≤0,
即
(t3-3t2)+(3t2+t-30)≤0,
因式分解,得 (t-3)(t2+3t+10)≤0.

0 于是x+y的最大值为3. 为了进一步掌握赛题解法的精髓,再举几例将赛题和解法进行拓展.事实上,赛题的约束条件和结论均可以适当放宽,但是解决问题的宗旨不变,解题策略仍然可以通过构造一元二次方程或换元、减元和不等关系进行统一求解.详情请参阅文献[2]. 例2若实数x,y满足x2-3xy+2y2=1,则x2+y2的最小值为______. 评注上述换元、减元和不等关系的联合使用,魅力十足.若考虑构造一元二次方程,则可设x2+y2=t=t·1=t(x2-3xy+2y2),操作性更强.更多变化请参阅文献[3]. 解设xy=t,则 x+y=4+2t2, 从而 例4已知实数a>0,b>0,且满足3a+b=a2+ab,则2a+b的最小值为______. 解设2a+b=t,代入3a+b=a2+ab,得关于a的方程a2+(1-t)a+t=0有正根,从而 Δ=(1-t)2-4t≥0且t>1, 即 t2-6t+1≥1, 由于赛题把不同的轮换对称式巧妙地融入条件和求解的结论之中,因此不难编制出系列预测性变式题. 变式2若实数x,y满足x3+y3+3xy=1,则xy的最大值为______;x3+y3的最小值为______. 变式3若实数x,y满足x3+y3-2(x2+y2)-7xy+3=0,则x+y的最大值为______;xy的最大值为______. 解设x+y=t,则 t(t2-3xy)-2t2-3xy+3=0, 即 (t+1)(t2-3t+3-3xy)=0, 故 化简整理,得 t2-12t+12≤0, 即 感兴趣的读者可以根据赛题的拓展思路编制更多的试题并研究更多的解法,从中感悟数学的简洁美、对称美以及数学的核心素养.最后,笔者把这两道赛题的联合研究拙见提出来,供大家研究. 猜想若实数x,y满足x3+y3+A(x2+y2)+B(x+y)+Cxy=D(其中A,B,C,D为常数),则xy,x+y,x2+y2,x3+y3的最大值或最小值中至少可以求得其中之一.3 赛题拓展


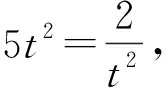

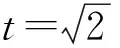
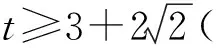
4 赛题变式