基于BT-SVM模型组合的动态加权多分类算法研究
李 涛,张景肖
(中国人民大学 a.应用统计科学研究中心;b.统计学院,北京 100872)
一、引言
近年来,随着信息技术的蓬勃发展,社会真正进入了大数据时代,人工智能(AI)也随之兴起。在AI领域的研究中,分类问题是备受关注的问题之一,而其中的多分类问题已越来越被重视。目前,针对多分类算法已取得了大量的研究成果,很多较为高效的多分类算法也已被应用到实践当中。经典的多分类算法主要是以“一对一”算法和“一对余”算法为基础,将多分类问题转化为多个二分类问题来实现,但“一对一”方法容易造成数据冗余,而“一对余”方法耗时较多、效率较低,两者都存在不可分区域和训练时间比较长的问题[1-2],因此需要开发新的更为高效和准确的算法。随着计算机硬件的发展,以Bagging和Boosting为代表的集成学习方法得到了迅速发展,经有关学者研究发现[3] 171-185,通过集成学习可以得出一个稳定且在各个方面都表现比较优良的模型。
随机森林和支持向量机(以下简称SVM)等是目前针对多分类问题应用最广泛的方法,其中以决策树为基学习器集成学习模型的随机森林是Bagging的典型代表,已引起了广泛关注,比如Bottou L等人从理论上深入研究了集成学习[4-7];黄衍等人从泛化能力、鲁棒性、对不平衡数据的分类有效性三个方面研究了随机森林和SVM的性质,研究结果表明:对于二分类,二者的泛化能力无显著差异;对于多分类,随机森林则稍优于SVM(“一对一”SVM多分类算法,“一对余”SVM多分类算法等),二者对数据类别噪声的鲁棒性无显著差异;在不平衡数据分类上,随机森林稍逊色于SVM[8]。因此,对于多分类问题,随机森林在泛化能力上比SVM更有优势,但在对不平衡数据的分类有效性上,随机森林却逊色于SVM,且随机森林在结果输出上采用简单投票法,若各类别得票数相差无几或者多个类得票数相同,结果将会有很大的随机性,可能导致分类精度下降。此外,在多分类算法上,GBDT(梯度提升树)的应用也较为广泛,但当数据量很大时,由于GBDT的弱分类器之间互相影响,无法真正做到并行化[9]。Maclin等人研究发现,一般情况下Bagging方法在改善系统性能方面较为稳定,而Boosting的结果反差较大,有效时优于Bagging,无效时却可能使学习系统恶化[10]。
近几年,基于二叉树算法的多分类模型备受关注,比如国内马景义等研究了基于二叉树算法的理论性质与实践[11]。与“一对一”算法和“一对余”算法相比,二叉树算法所需要的分类器更少,计算的复杂度更低并且没有识别盲区[12]。鉴于此,本文将基于二叉树多分类算法和SVM的特性以及多分类器集成的优势[13-14],以BT-SVM(基于二叉树算法的SVM多分类模型)为基分类器,提出一种带阈值的新型动态加权多分类器集成的方法。
二、基于BT-SVM组合的新型动态加权多分类算法
(一)基于二叉树算法的SVM多分类模型
二叉树算法类似于排序算法中的“快速排序”:首先将所有的类别按照某一规则划分成两个大的类别,然后对已有类别再按照一定规则继续划分,直到所有的节点只含有一个类为止。常见的BT-SVM有两种结构:一是偏二叉树结构,在每一个内部节点由一个类与剩余类构造分割面,如图1(左)所示;二是“平衡”二叉树结构,在每一个内部节点可以是多个类与多个类的分割,如图1(右)所示。本文主要考虑前一种结构,每次分割只能分割出一个类,但此种结构不同的层次可能产生不同的精度,因为存在“错误累积”现象,若在某个节点发生分类错误,则错误将一直延续,因此须选择合理的层次结构。
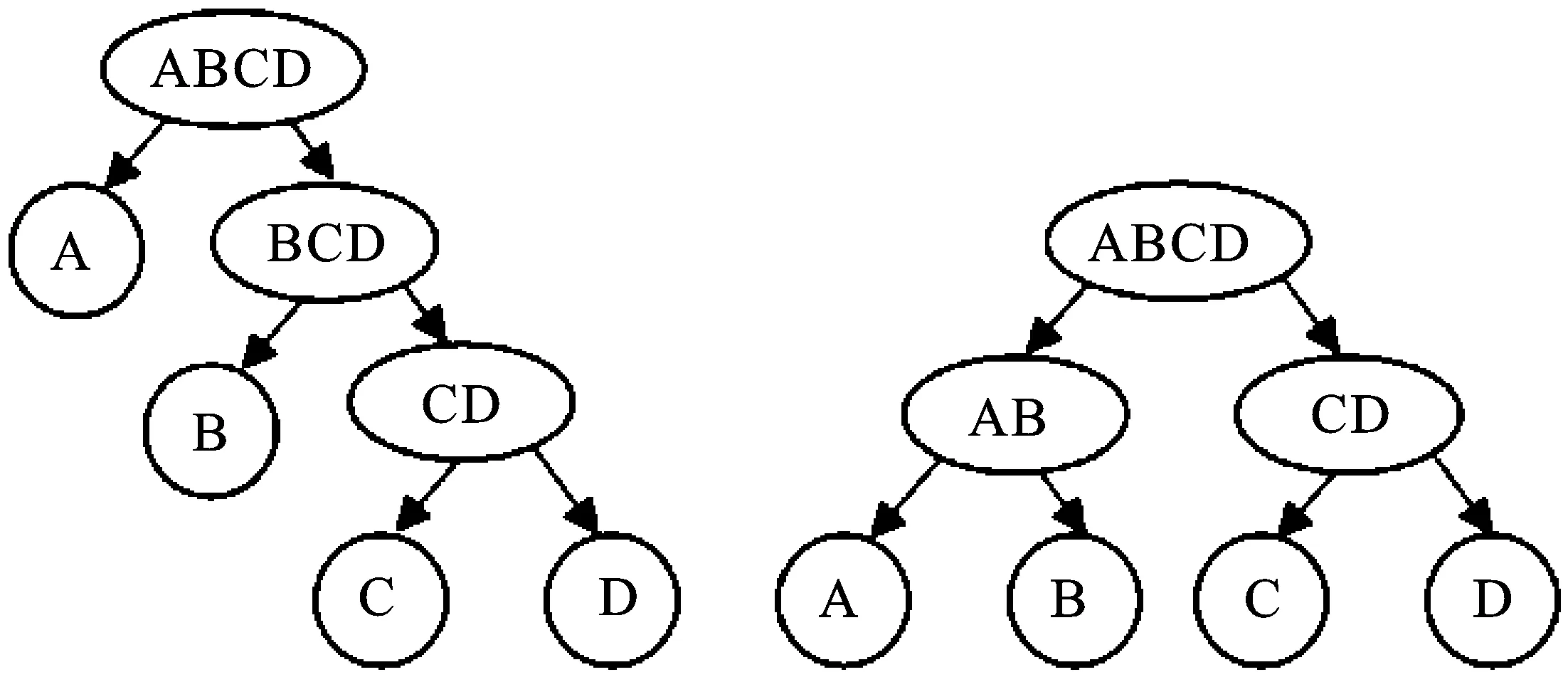
图1 BT-SVM的不同结构图
目前,最常用的BT-SVM生成算法是聚类分析中的类距离法,而类与类之间的距离选择将对结果产生很大影响,常用的距离有最长距离、最短距离等。本文采用类中心距离:首先计算出每个类的类中心到其它类中心的距离之和,再选出与其它类距离最远的类进行分割,旨在将离其它类最远的类率先分离出来,此时BT-SVM具有最优分类精度,类间距定义如下:
其中mi为第i类的类中心,即类均值向量;这里的mi表示经过标准化或者中心化的原始类中心,已经取消了量纲影响。
(二)基于BT-SVM组合的动态加权多分类算法思想
对于SVM多分类问题研究,常用的是基于“一对一”算法的SVM多分类模型和基于“一对余”算法的SVM多分类模型。2010年,Jin-Long An和Zhen-Ping Ma提出了一种基于二叉树算法的SVM模型[1],与“一对一”算法、“一对余”算法相比,二叉树算法所需要的二分类器更少,计算复杂度也更小(见表1)。

表1 三种多分类算法比较表
房汉鸣等研究指出,二叉树算法也可较好解决“一对一”算法、“一对余”算法中存在的识别盲区,即不可分区域的问题[12]。

图2 三种多分类算法示意图
基于Bagging集成思想,利用BT-SVM的精度较高、复杂度小等特性,本文以BT-SVM为基分类器和多分类器组合的方法进行研究。在多分类器集成系统中,一个关键的问题是如何综合各分类器结果,其中最常用的是简单投票的策略,如随机森林。然而,当各分类器性能不统一时此种做法往往造成较大的负面效果,尤其在出现各类别得票数相差无几或多类得票数相同的情况时,如果还采用之前的简单投票进行预测,则预测准确性将大打折扣。
综上所述,本文基于BT-SVM,提出一种带阈值的新型动态加权多分类器集成方法:将BT-SVM作为基分类器,利用训练集生成若干个分类器,将待测样本带入各个分类器得到结果,再通过给定阈值判断是否加权;如果低于阈值,那么将进行动态加权给各个基分类器分配对应的权重。本文利用KNN思想,从样本中选出与待测样本相似的K个样本代入已训练好的分类器得到错分率,并利用错分率得到各个分类器的权重,最后进行线性加权,求出最优的识别结果。
(三)基于BT-SVM组合的新型动态加权多分类算法的具体流程
基于BT-SVM组合的新型动态加权多分类算法具体算法流程如下所述:
Step1:进行数据预处理与特征提取。如缺失值异常值的处理、特征的分解与合并等,然后进行特征选取,选取相应的特征作为特征向量。
Step2:训练L个分类器(L事先给定)。借鉴Bagging的思想,对于每个分类器BT-SVM,从训练集中采用有放回抽样抽取M个样本,按照前文所述的BT-SVM生成算法,代入每一个分类器中得到L个训练好的分类器,记为DT_SVMi,i=1,2,…,L。
Step3:将待测样本输入L个分类器中得到初步识别结果。处理数据后,将相应的特征向量代入到step2中训练好的L个分类器DT_SVMi中,每个分类器DT_SVMi会得到相应的分类结果,最终得到L个分类结果,记为Rei,i=1,2,…,L。给定阈值C(百分比一般情况下尽可能设置为较大的值),若L个分类器有超过C的分类器得到相同分类结果,则直接输出结果,否则进行step4。
Step4:动态获得每个分类器的权重,每个分类器线性加权得到最终分类结果。 计算特征向量间的欧式距离(若全为离散值,则给出Kmodes距离),利用KNN思想,找到与待测样本最相似的K个近邻,将K个近邻代入每个训练好的分类器DT_SVMi;对于每个分类器DT_SVMi将得到K个结果,计算相应的错误率Eri,i=1,2,…,L。
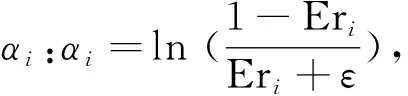
三、数值模拟
本节通过数值模拟,以分类准确率和F1Score值作为指标,将本文所提出的方法与当前最常用的随机森林和GBDT进行比较。
(一)实验平台与数据生成
本实验使用的操作系统为Mac 10.11.6,实验软件平台为Python3.6(IDE:Anaconda)。本实验模拟生成了5 000个样本,共有8个特征变量(包含常见的数据分布)和1个分类变量,分别记为X1,X2,…,X8和Y′,其中X1~X2服从伯努利分布、X3~X5服从正态分布、X6~X7服从泊松分布、X8服从均匀分布;ε~N(0,1)是随机扰动项,Y′=X1+X2+…+X8+ε。根据Y′的分位数生成分类变量,分别生成4类别、8类别、10类别的平衡数据与非平衡数据。
(二)评价指标
考虑到多分类问题,本文采用了分类准确率和F1Score值作为评价指标。如果单纯只考虑分类准确率这一个指标,衡量非平衡数据的算法有效性是远远不够的。F1Score值是精准率和召回率的综合结果,具体定义如下:
其中精准率是描述模型预测正确的正样本数与模型预测的正样本数之比,用来衡量模型预测正样本的准确性;召回率是模型预测正确的正样本数与实际正样本数之比,以此衡量模型预测正样本的可信性。
(三)结果分析
将4类别、8类别、10类别的数据代入基于BT-SVM组合的新型动态加权多分类算法、随机森林和GBDT3个模型中,其结果见表2。
无论从样本类别分布(平衡数据与非平衡数据)还是样本类别数(4类别、8类别、10类别)看,基于BT-SVM组合的新型动态加权多分类算法在分类准确率上和在F1Score上,其表现都较随机森林和GBDT更优,尤其是相较同样出身于Bagging家族的随机森林而言,有较大的优势。另外,单从准确性看,三个模型在平衡数据中的表现都要优于其自身在非平衡数据中的表现。
四、实证分析
以上利用数值模拟技术对比了三个模型的性能,以下主要利用UCI数据集库中实际数据来补充验证模型的性能。
(一)实例数据来源及其介绍
本次实证所使用的数据来自UCI数据集库中的多类数据,UCI数据集是用于机器学习的公共数据库(http://archive.ics.uci.edu/ml/index.php),本文所应用的数据集为Glass数据集和Ecoli数据集(见表3)。

表3 数据集介绍表
(二)数据预处理与数据可视化
由于本章所用数据集均采自UCI数据库,没有缺失值等情况,故无需做相应的数据清洗,而且作为分类任务,无需考虑变量之间的相关性和共线性等问题,因此选择全部特征作为分类的特征向量。
本文利用多维数据可视化算法T-SNE(实际上T-SNE是一个降维算法,实际中却被用作高维可视化工具,T-SNE利用条件概率,将高维空间数据之间的相对距离压缩到二维或者三维空间上展示,数据之间的相对位置不变),并利用T-SNE可以展示数据间的相对位置,从而粗略观察各类别的数据分布情况(见图2图3)。
由图2图3可知,Ecoli数据集比Glass数据集的类区分度更高,如果用同一种模型来做分类,在Ecoli数据集上的效果将会比Glass数据集的好。
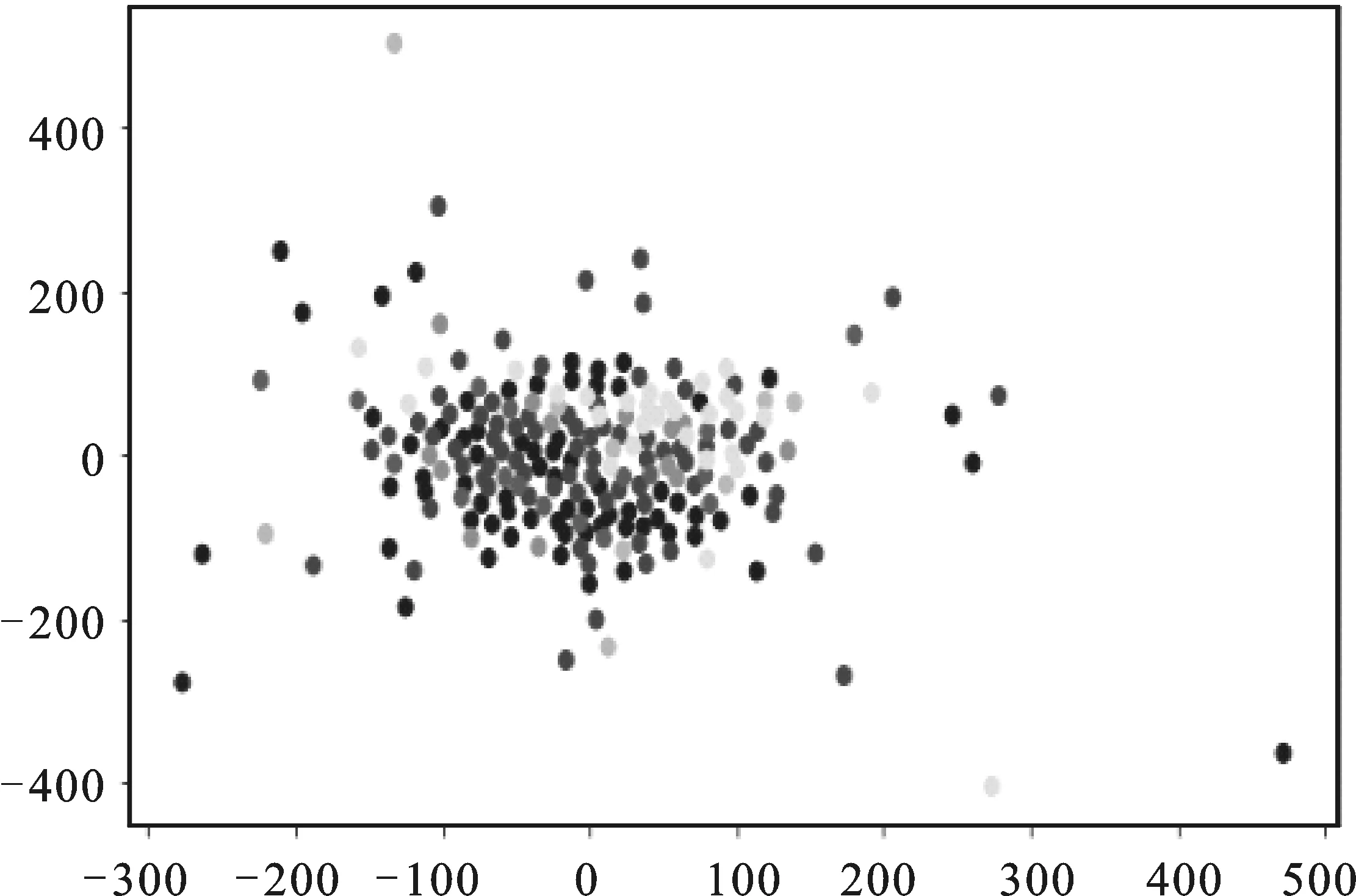
图3 Glass数据集样本分布图

图4 Ecoli数据集样本分布图
(三)结果与分析
将Glass数据集和Ecoli数据集代入基于BT-SVM组合的新型动态加权多分类算法、随机森林和GBDT三个模型中,其结果见表4。

表4 基于BT-SVM组合新型加权动态多分类模型、随机森林和GBDT模型对比表
从Glass数据集的应用结果看,基于BT-SVM组合动态加权模型、随机森林和GBDT在分类准确率上平均结果分别为0.74、0.63、0.69,在F1Score上平均结果分别为0.65、0.36、0.61。基于BT-SVM组合动态加权模型在两个指标上都优于随机森林和GBDT;而对于Ecoli数据集的应用结果,基于BT-SVM组合动态加权模型、随机森林和GBDT在分类准确率上平均结果分别为0.87、0.86、0.87,在F1Score上平均结果分别为0.68、0.53、0.56。基于BT-SVM组合动态加权模型在分类准确率指标上与随机森林和GBDT相差不大,但基于BT-SVM组合动态加权模型在F1Score值指标上较随机森林和GBDT更为优良;在多分类中,不仅要看分类准确率,还要关注精准率和召回率,因其分别体现了预测正样本的准确性和可信度,尤其是在非平衡数据中;GBDT是串行的,基分类器互相影响,不能做到并行,但该算法可以做到并行化,这在应用上的优势是非常明显的。
综上所述,基于BT-SVM组合动态加权模型表现优于随机森林和GBDT。
五、结论与展望
本文从多分类的背景与意义出发,介绍了BT-SVM的定义及其与常见的多分类算法相比较的优势,并简述了当今主流多分类算法随机森林在输出结果方面的缺陷以及GBDT无法真正并行化和不稳定等情况;基于Bagging的并行化思想,进而提出了一种以BT-SVM为基分类器、多分类器组合的带阈值的新型动态加权模型,并且进行了数值模拟和实证研究检验其效果。本文从分类准确率和F1Score值两个指标综合考虑,结果显示无论在数值模拟还是实证研究上,本文提出的模型在分类准确率和F1Score值上取得的结果都比随机森林及GBDT有不少的优势。
由于BT-SVM的自身结构是二叉树模型,如果在上一个节点分类错误将会一直延续,因而会存在错误累积的现象。对于类别数很多的情况(数值模拟中20类以上),精度可能不会太高,之后需要改进BT-SVM的错误累积现象,则可以从类间距的定义出发,容易区分的类最先被分离,也可以采用类似基于平衡二叉树算法的SVM,以此改善错误累积的现象。

