扩散对流温盐台阶结构的数值模拟

徐岩, 刘香全, 3, 4, 宋仁刚, 岑显荣, 郭双喜, 周生启



扩散对流温盐台阶结构的数值模拟

徐岩1, 刘香全1, 3, 4, 宋仁刚1, 岑显荣2, 郭双喜2, 周生启2

1. 山东科技大学 电子通信与物理学院, 山东 青岛 266590; 2. 热带海洋环境国家重点实验室(中国科学院南海海洋研究所), 广东 广州 510301; 3. 中国科学院半导体研究所 集成光电子学国家重点实验室, 北京 100083; 4. 中国科学院大学 材料科学与光电技术学院, 北京 100049

热盐驱动下的扩散对流现象是海洋中高纬度海域普遍存在的一种现象, 对其进行数值模拟可更细致地研究海洋小尺度动力过程。文章分析了扩散对流的形成机制, 建立了二维方腔模型, 通过有限体积法求解控制方程, 对其分层现象进行了数值模拟。研究给出了流场的温度及盐度随时间演化的关系, 展现了流场中速度的涡旋结构, 分析了温盐台阶结构的生成、合并的演化过程, 并对其物质和能量的输运进行了初步的理论解释。另外, 对不同热流密度情况下的扩散对流现象进行了对比研究, 发现随着热流密度的增加, 台阶结构的演变速率变快, 而且上边界冷却对其演化速率具有促进作用, 但热流密度的改变并没有对台阶结构的演变趋势产生明显的影响。

扩散对流; 温盐台阶; 盐度; 温度

在自然界及工业生产中存在着诸多的双扩散现象, 如海洋中受温盐共同作用的扩散对流及盐指现象, 地壳中软流层的运动, 大气中热和污染物的扩散, 工业生产中晶体的成长、金属的固化等(郑珺婷等, 2002)。当流体中的两种(或多种)组分具有不同的扩散率时, 容易产生双扩散现象。在海洋环境中, 海水的热扩散率(≈1.4×10-7m2·s-1)比盐扩散率(≈1.4×10-9m2·s-1)大两个量级, 且当两者对海水的密度梯度的贡献作用相反时, 在热驱动和盐驱动下形成双扩散对流, 从而促进海洋内部混合, 并进一步影响着海洋中物质和能量的输运(Schmitt, 1994)。

在双扩散的室内实验中, 线性层结的盐水系统在底部加热、顶部冷却时, 会产生明显的温盐台阶结构, 形成“扩散成层”现象(Turner, 1968; Huppert et al, 1979; Lewis et al, 1982; 万伟等, 2014; Guo et al, 2016)。在海洋中, 当低温低盐的水位于高温高盐的水之上时, 就会产生扩散对流现象, 在温盐廓线中呈现台阶结构(鲍征宇, 1989; Guthrie et al, 2015; Kimura et al, 2015; Xie et al, 2015; Zhou et al, 2016; Bebieva et al, 2016; Shibley et al, 2017; Guthrie et al, 2017), 如图1a所示。具体形成机制如下: 如图1b所示, 在界面之下的高温高盐海水受到扰动, 从暖而咸的深层环境进入到界面之上的冷且淡的浅层环境, 由于热扩散速率较大, 该海水微团就会迅速地向周围环境释放热量, 直至温度降低到与周围海水微团温度相同。但是此时由于盐扩散速率较小, 使得该海水微团基本保持原来的盐度不变, 深层的海水微团上升一段距离后, 与周围海水微团密度一致; 若上升的距离较大, 使该海水微团的密度大于周围海水微团, 则海水微团在重力的作用下向下运动, 最终达到比较稳定的状态, 形成有限高度且相对均匀的对流层。类似地, 界面上的低温低盐的海水微团受到扰动, 从冷而淡的浅层环境进入界面之下的暖而咸的深层环境, 由于受热而密度不断减小, 在下降一段距离后, 密度与周围海水一致, 之后继续吸收热量而密度重新变小, 微团又开始向上运动。如此反复, 在界面的上下形成了对流混合层。混合层内的温度、盐度和密度均匀, 以对流运动为主; 界面处则具有较大的梯度, 以分子扩散运动为主, 最终形成台阶结构。

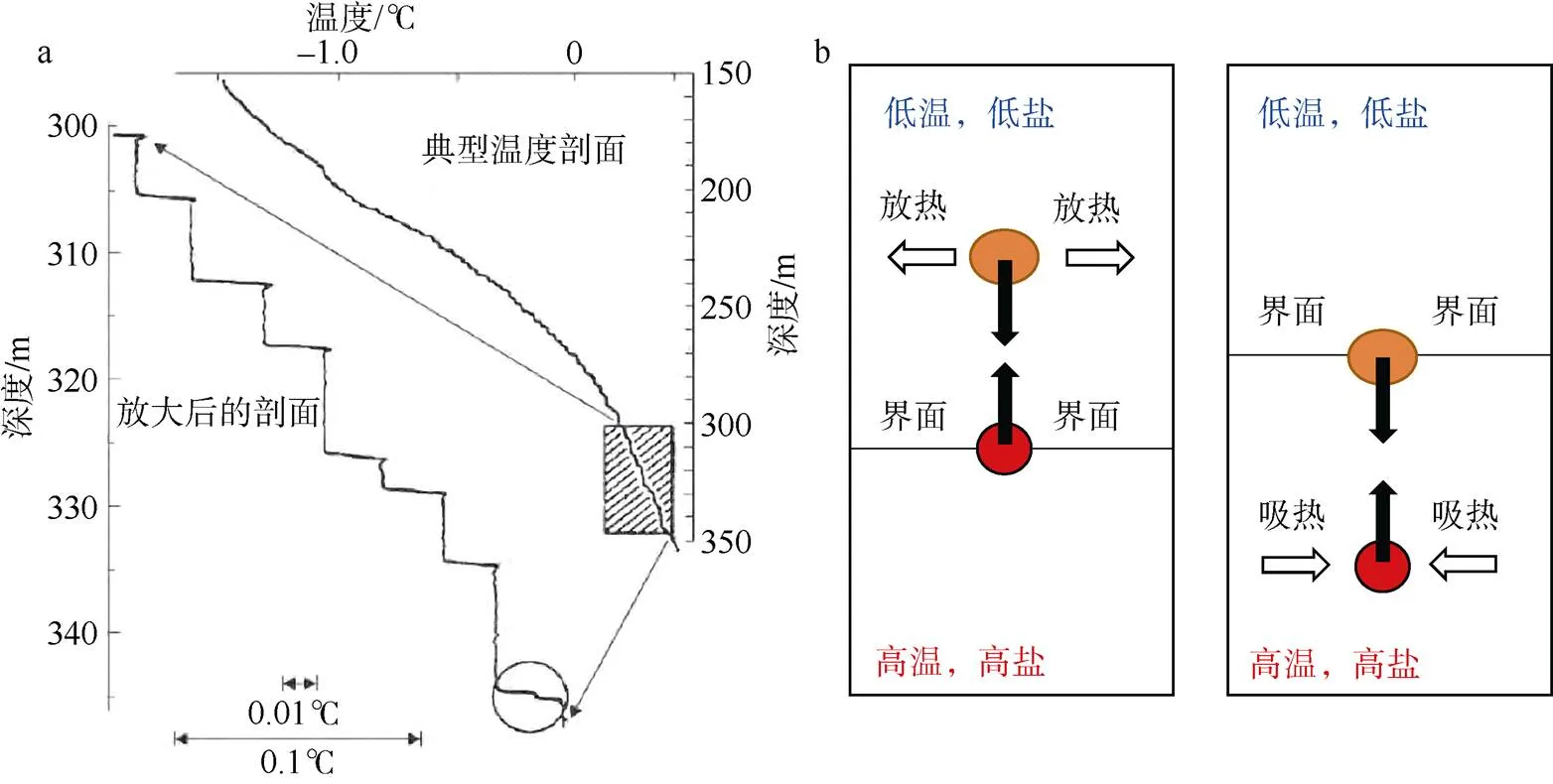
图1 扩散对流

a. 北冰洋的温度台阶结构(Neal et al, 1969)。图中的矩形阴影表示需要放大后才能观察到温度台阶结构的剖面, 圆环表示温度台阶界面的双层结构。图的左下横轴(双箭头线)的长度表示温度的涨落幅度; b. 扩散对流形成机制示意图

Fig. 1 Thermal staircases in the Arctic Ocean (a), and illustration of formation mechanism of diffusive convection (b)

在对温盐台阶问题的研究中, 人们采用了多种方法, 如流体力学室内实验、海洋现场观测以及数值模拟等。Turner等(1964)通过实验演示了温盐台阶结构的生成过程, 并对其进行了定性的描述。1968年, Turner (1968)通过实验, 发现了第二个混合层出现之前, 第一个混合层的厚度和第一个扩散界面的温差、盐度差随时间的变化与1/2的标度律相符合, 且对第二个混合层出现的临界条件进行了研究。1972年, Huppert等(1972)的研究表明, Turner在室内实验进行的温盐台阶结构研究得到的热通量经验公式可应用于海洋中大尺度流动的研究。这些研究确立了扩散对流温盐台阶热通量的基本规律, 即和温差的4/3标度律。Marmorino等(1976)以及Kelley (1990)根据室内实验数据, 指出每个台阶都可以理解为一个包含对流环的对流层, 并确定了热通量和密度比的关系, 进而完善了热通量参数化方案。Carpenter等(2012)利用直接数值模拟方法研究了扩散对流界面的动力过程, 发现界面的热输运以分子热扩散为主。Guthrie等(2015)利用北冰洋扩散对流的观测数据对Kelley(1990)的参数化方案进行了验证。以上的这些工作主要关注扩散对流的界面稳定性及热通量问题, 而对于台阶演化的完整过程还有待做进一步的细致研究。

本文在前人的基础上, 通过数值方法模拟了扩散对流台阶结构的生成、演化、合并以及最后消失的整个过程。通过设置不同边界条件, 来讨论热流密度对扩散对流台阶结构演变速率的影响规律。

1 模型建立

1.1 物理模型

用数值计算的手段对扩散对流进行模拟具有多种优势, 能够精确地描述流场及标量场, 且严格控制边界条件(邢元明等, 2013)。Turner(1965)指出, 双扩散的稳定性可以用密度比进行衡量, 定义如下:

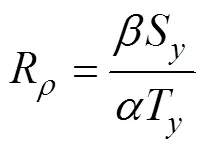
式(1)中,为温度,为盐度,为流体密度,=-(1/)∂/∂和=-(1/)∂/∂分别为热膨胀系数和盐收缩系数,S=∂/∂和T=∂/∂分别为盐度和温度的垂向梯度。定义为流体盐扩散率与热扩散率之比, 即=, 普朗特数=/为流体黏性与热扩散率之比。线性稳定理论表明, 1<R<(+1)/(+)是双扩散不稳定性发生的条件。在海洋中, Kelley等(2003)认为当密度比R在1~10范围内时, 温盐台阶结构更容易产生, 并且当它越接近于1时台阶结构越明显(Kelley et al, 2003; 屈玲, 2014)。

到目前为止, 对双扩散的理论研究, Boussinesq模型得到了广泛的认可。Boussinesq假设认为密度的变化并不显著改变流体的性质(赖锡军, 2004); 同时，在动量方程中, 密度的变化对惯性力项、压力差项和黏性力项的影响可忽略不计, 而仅考虑其对质量力项的影响。假设流体为不可压缩流体, 密度的线性状态方程为:

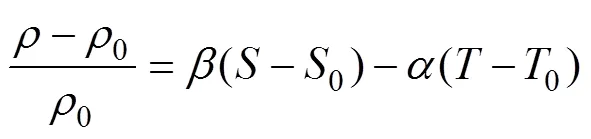
表达式(2)中,0、0、0分别代表参考温度、参考盐度及参考密度。

在Boussinesq假设下, 双扩散系统的控制方程为:

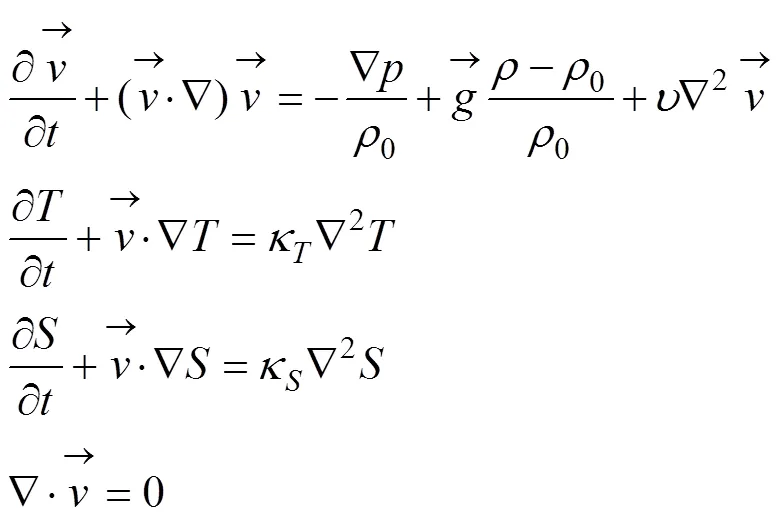
1.2 数值方法

建立扩散对流的二维方腔模型, 如图2所示。设定其长和宽均为10cm, 底部加热, 顶部冷却(即底部和顶部施加固定热流密度边界条件), 左右壁面为绝热壁面, 满足∂/∂=0, 各边界为无滑移边界, 且满足∂/∂=0 (詹杰民等, 2002; 卢玉华等, 2006)。考虑重力的作用, 其方向为沿轴的负方向。设定初始盐度随高度线性递减, 初始温度则均匀分布, 由此形成线性层结的初始密度分布。

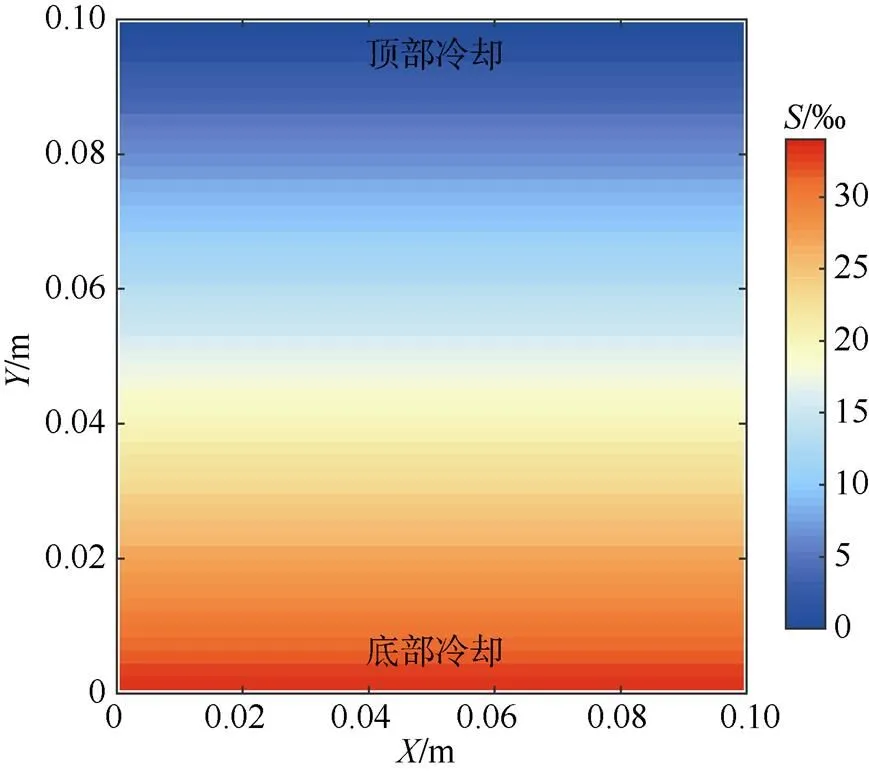
图2 扩散对流数值模型

控制方程的离散采用有限体积法, 为了在保证计算稳定性的前提下尽量提高计算精度, 本文在计算时对于扩散项采用一阶迎风格式, 而对流项则采用中心差分格式; 在时间离散方面, 传统的三时间层蛙跳格式在气象和海洋数值预报中使用较广泛, 但存在计算解及时间滤波的精度降阶问题, 为弥补此不足, 可采用回溯时间差分格式(Feng et al, 2001)或Adams-Bashforth格式(Durran, 1991)等替代方案。本文采用Adams-Bashforth格式, 相比蛙跳格式它能更大程度地保持方程组的计算准确性。计算在方形网格上进行, 网格数为100×100, 时间步长设为0.01s。在扩散对流模拟中, 设二维方腔中的初始温度为参考温度(300K), 顶部的初始盐度为0, 底部的初始盐度为34‰。

用Paraview软件对结果进行后处理时, 盐度在0~34‰范围内等间距的取50条等值线, 绘制中截线(=5cm)上的盐度变化曲线。

2 结果与讨论

2.1 台阶结构的演化过程

当加热和冷却的热流密度均为2200W·m-2时, 观察二维方腔系统盐度的变化, 情况如下(图3):

当时间为0.169h时, 双扩散不稳定性开始发生, 在方腔的顶部和底部出现了羽流结构; 时间为0.433h时, 顶部和底部已出现了明显的台阶结构, 在高度约为1.1cm、1.9cm、8.2cm、8.9cm处出现4个较为明显的扩散界面, 1.9~8.2cm的中间部分盐度仍呈线性分布。这些台阶结构基本是关于=5cm这条直线对称的, 这是由于模型的边界设置的对称性所致。

当时间约为0.839h时, 在高度约为1.7cm、2.3cm、3.2cm、6.9cm、7.7cm、8.4cm位置处出现了6个扩散界面, 较之前相比, 两个主稳定层(最底和最高的均匀层)的厚度增加了, 而两个次稳定层(顶端主稳定层的下端, 底端主稳定层的上端)的厚度减小了。

当时间为0.989h时, 在高度约为1.8cm、2.4cm、3.2cm、3.9cm、6.2cm、6.7cm、7.5cm、8.1cm位置处出现了8个扩散界面, 3.9~6.2cm的中间部分盐度仍呈线性分布, 但是临近界面处有了波动。

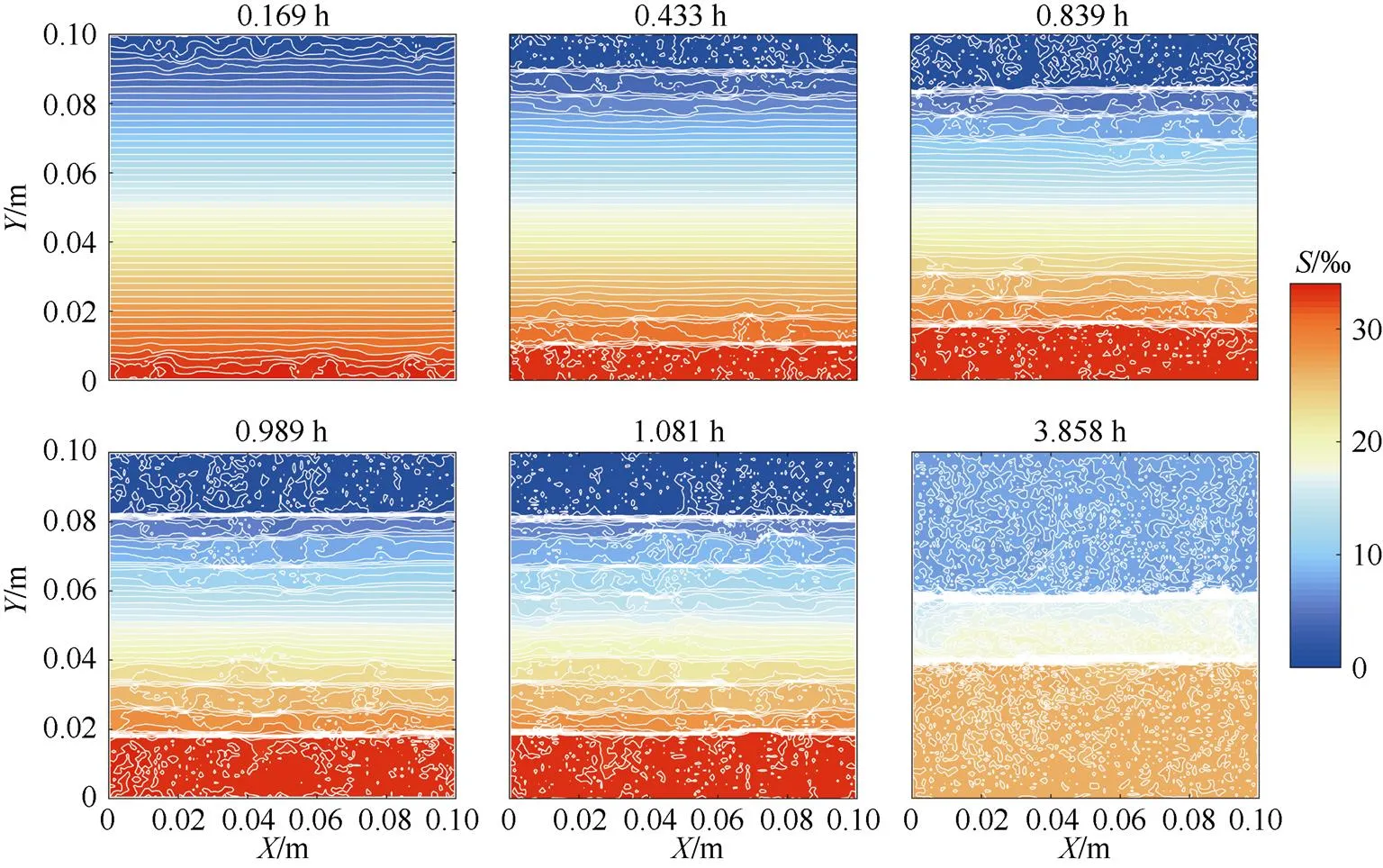
图3 扩散对流模拟不同特征时刻的盐度分布图

当时间为1.081h时, 在高度约为2.0cm、3.2cm、4.1cm、4.5cm、6.0cm、6.6cm、8.0cm位置处出现了7个扩散界面; 当时间为1.392h时, 在高度约为2.2cm、3.4cm、4.3cm、5.4cm、6.5cm、7.8cm位置处出现了6个扩散界面, 存在着7个盐度相对均匀的阶层, 中间均匀层的厚度基本相同, 如图4所示。在接下来约0.5h内, 扩散对流保持着相对稳定性, 台阶的数目和厚度基本不变。随着主稳定层的不断增厚, 两个次稳定层的厚度不断减小。

当时间约为1.989h时, 上下端的次稳定层消失, 只剩下5个相对稳定的阶层。当时间约为2.747h时, 下端新的次稳定层消失, 剩下4个相对稳定的阶层, 如图5所示。当时间为3.858h时, 上下两端的主稳定层向中间扩展, 变成3个相对稳定的阶层。中间稳定的阶层不断缩小。当时间约为4.811h时, 中间均匀层消失, 变成2个相对稳定的阶层, 如图6所示。然后扩散界面的位置基本保持不变, 上下两层的盐度差逐渐减小。当盐度差减小到一定程度时, 交界面向上移动, 盐度差依然在减小, 当时间约为17.106h时, 只存在一个稳定的均匀层, 整个体系的盐度为17‰。Carpenter等(2012)在两层“耗尽” (“run-down”)模拟实验中也关注了扩散对流的演化过程: 在“耗尽”实验中, 上下层台阶是自由发展的,期间扩散界面的温差和盐度差均逐渐减小, 密度比不断增大。相比之下, 本文模拟的扩散对流的演化经历了主稳定层的不断扩展和次稳定层的不断消失, 期间扩散界面的温差基本维持不变而盐度差逐渐减小, 密度比不断减小, 与“耗尽”实验的演化机制有所区别。

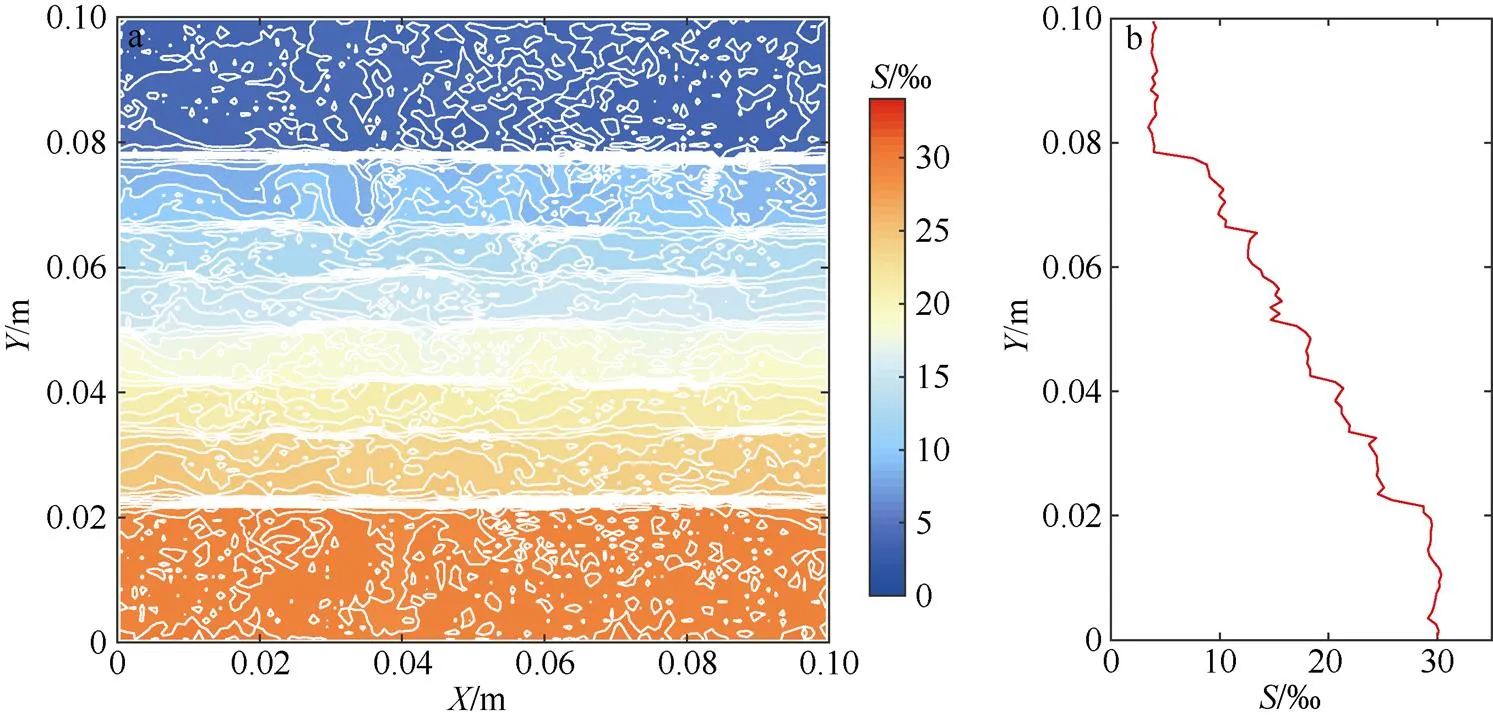
图4 扩散对流模拟1.392h后盐度状态图

a. 等值线图; b. 曲线图

Fig. 4 Salinity distribution after 1.392 h in diffusive convection simulation: (a) contour plot, and (b) line plot

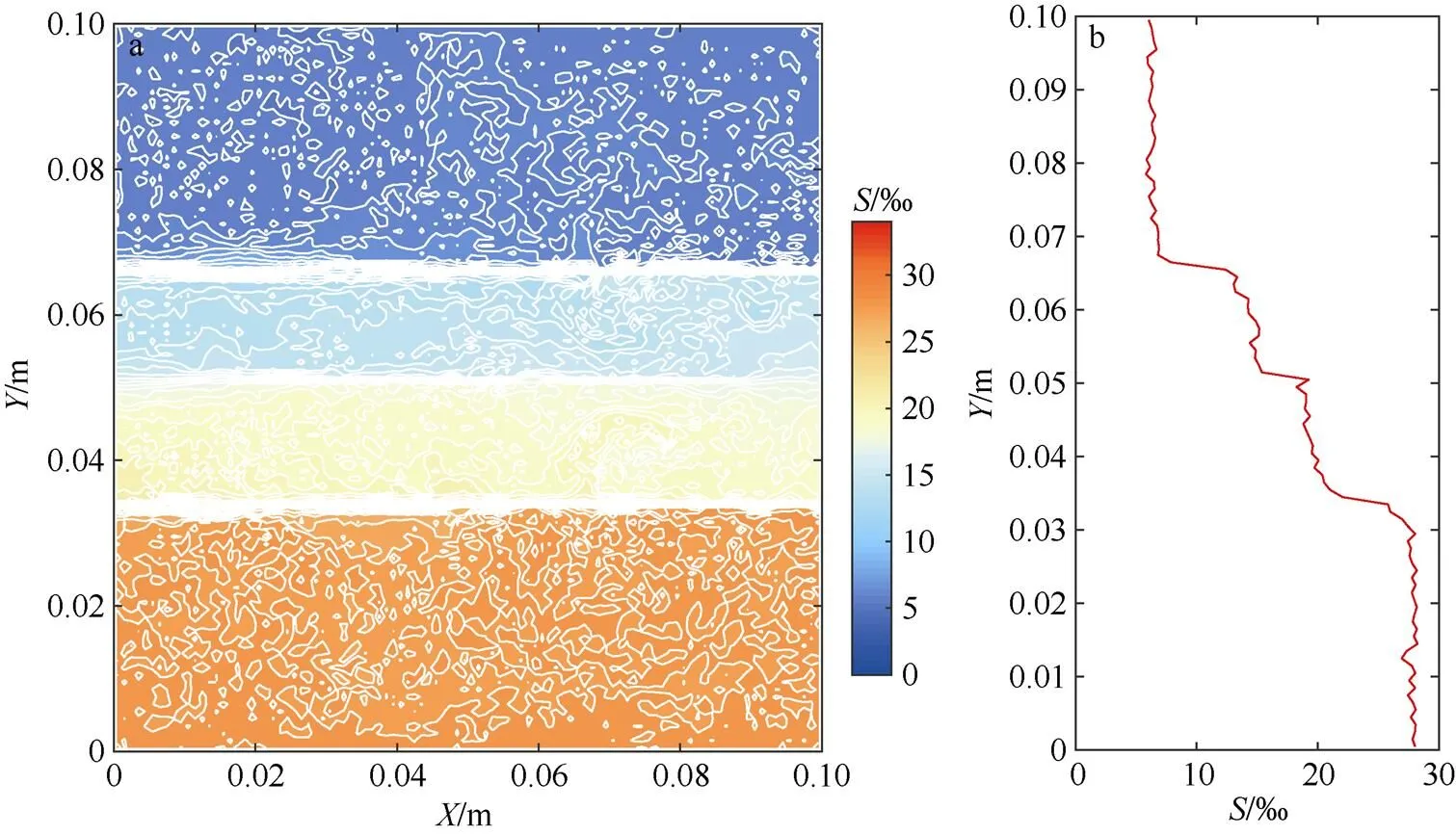
图5 扩散对流模拟2.747h后盐度状态图

a. 等值线图; b. 曲线图

Fig. 5 Same as Fig. 4, except after 2.747 h

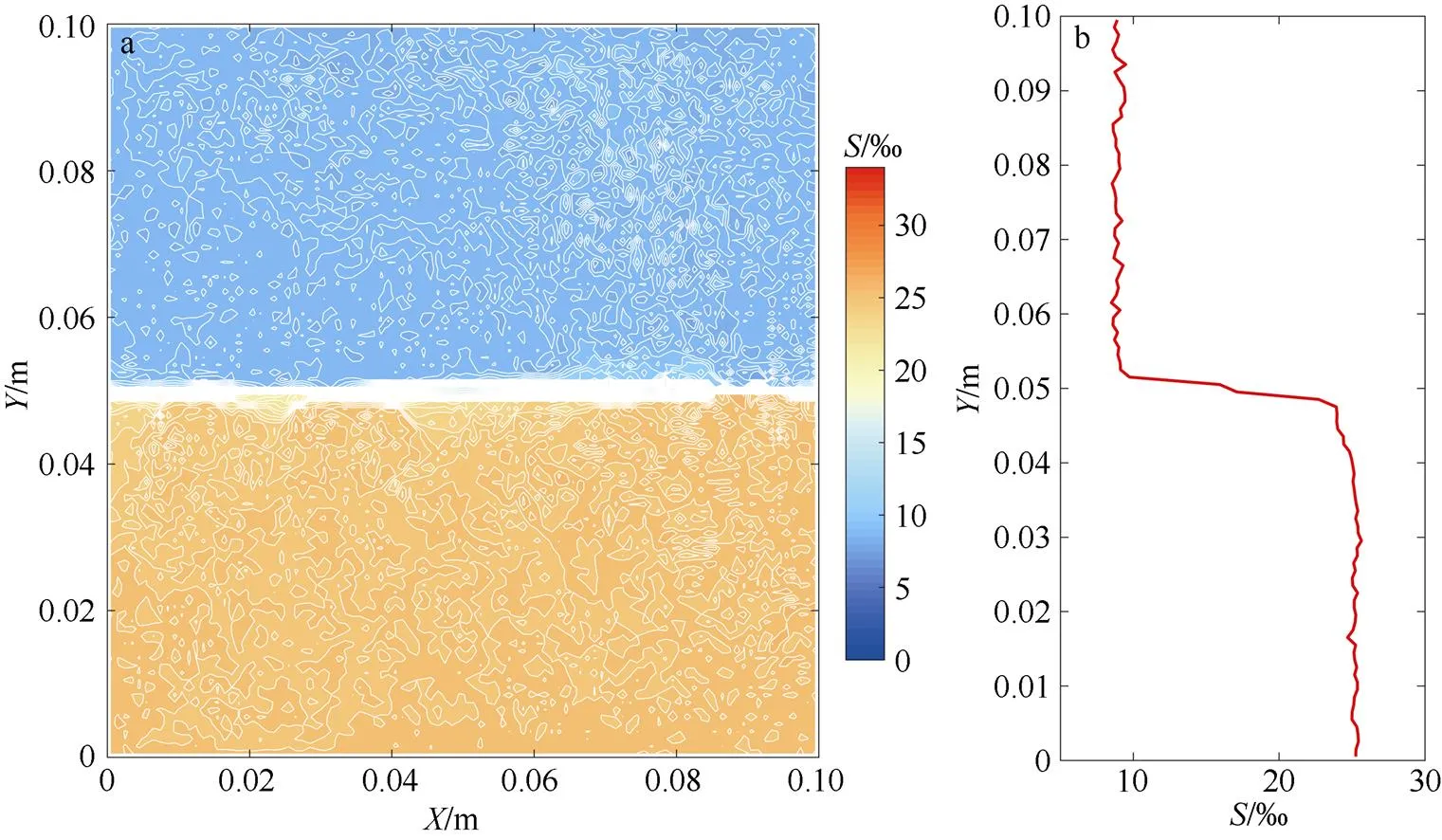
图6 扩散对流模拟4.811h后盐度状态图

a. 等值线图; b. 曲线图

Fig. 6 Same as Fig. 4, except after 4.811 h

在模拟过程中, 观察二维方腔系统温度的变化, 发现温度曲线的变化趋势与盐度曲线的趋势基本是一致的。万伟等(2014)在扩散对流的室内实验中也观察到了类似的温度台阶演化过程, 但由于缺少速度测量, 无法展现扩散对流的涡旋结构, 而本文的模拟工作可以弥补这些不足。观察二维方腔系统流场速度的变化, 流速场中不断伴随着涡旋的生成与消亡。选取4.811h时的速度分布矢量图, 如图7a所示, 在扩散交界面处流动较为微弱, 说明在扩散界面内部主要以分子扩散的形式输运物质, 以分子热传导的形式输运热量; 而在均匀的混合层内部涡旋较为明显, 说明主要以对流的形式输运物质和能量。选取17.106h时的速度矢量图, 如图7b所示, 此时整个系统的温度和盐度达到均匀稳定状态, 形成了一个大尺度的环流。

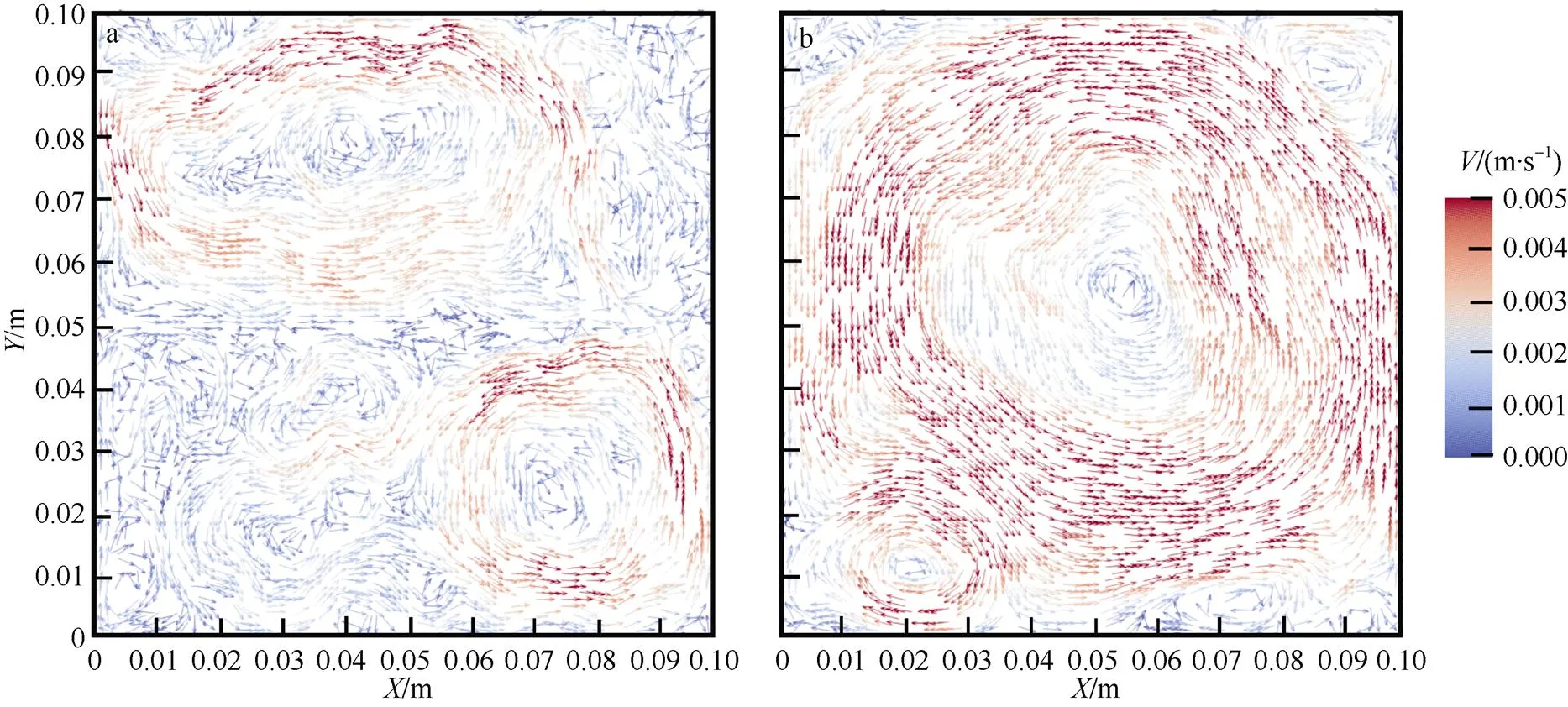
图7 流场速度分布矢量图

a. 4.811 h时; b. 17.106 h时

Fig. 7 Vector plot of simulated velocity field: (a) 4.811 h, and (b) 17.106 h

2.2 不同热流密度下对比讨论

本模拟在对二维方腔上下边界的加热和冷却设置时, 选取了不同的热流密度。具体设置情况如下。

情况①: 上下热流密度均为1000W·m–2;

情况②: 上下热流密度均为2200W·m–2;

情况③: 上下热流密度均为3000W·m–2;

情况④: 上冷却热流密度为1000W·m–2, 下加热热流密度为2000W·m–2。

我们关注不同工况下温盐台阶的数目随时间的变化规律, 模拟结果如图8所示。

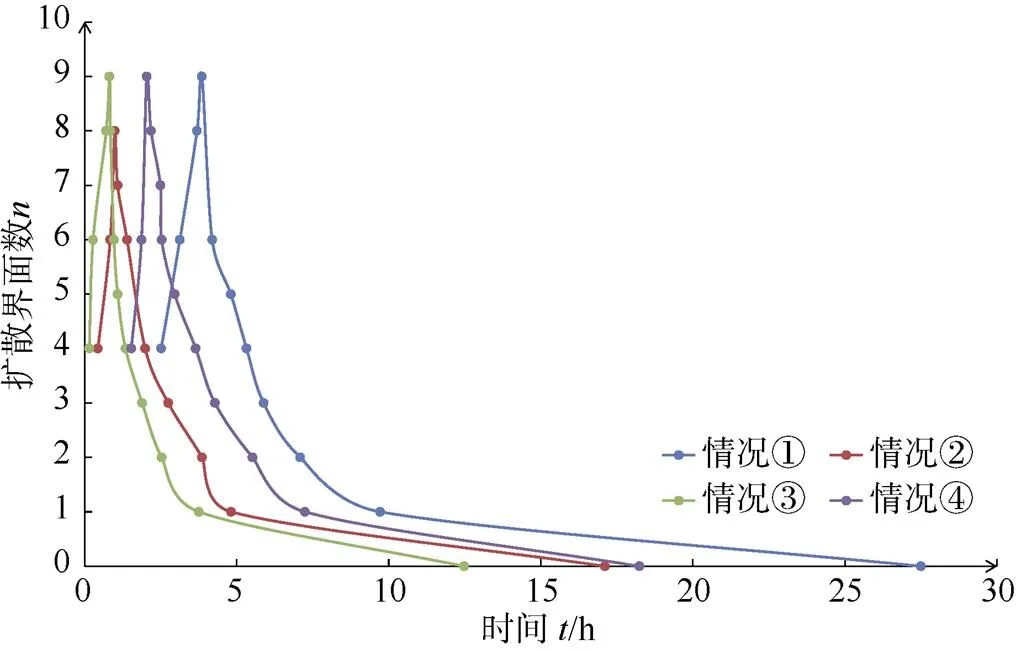
图8 不同热流密度下扩散对流温盐台阶结构模拟结果对比

情况①—③中的上下边界热流密度在数值上具有对称性。在图8中可以看出, 与情况②的模拟结果相比, 情况①出现相同扩散界面的时间明显增加, 说明台阶结构的生成及合并速率明显减慢; 情况③的台阶结构的生成及合并速率明显加快, 演变时间明显变短。由扩散界面的变化趋势可以看出, 在这3种情况下, 台阶结构的演变过程是类似的, 前期是台阶结构的增加, 后期是台阶结构的合并, 但台阶的数目及速率存在差异。

情况④中, 由于下边界的热流密度值比上边界更大, 扩散对流温盐台阶结构的对称性被打破。情况④与情况②相比, 在下边界加热热流密度接近, 上边界冷却热流密度差一倍的情况下, 情况②的曲线位于情况④曲线的左侧, 如图8所示, 表明情况②相同扩散界面出现的时间短, 演变速率较快。该现象说明了情况②中上边界较大的冷却热流密度对温盐台阶结构的演化具有一定的促进作用。但是这两种情况扩散界面数随时间的演化趋势是类似的, 并没有明显的不同。另外, 情况④在台阶演变过程中, 下方主稳定层的厚度一直大于上方主稳定层的厚度, 台阶结构不再是上下对称的形式, 如图9所示, 该现象是由于上下边界热流密度不同所致, 下边界较大的热流密度使得下方主稳定层具有较快的演变速率。

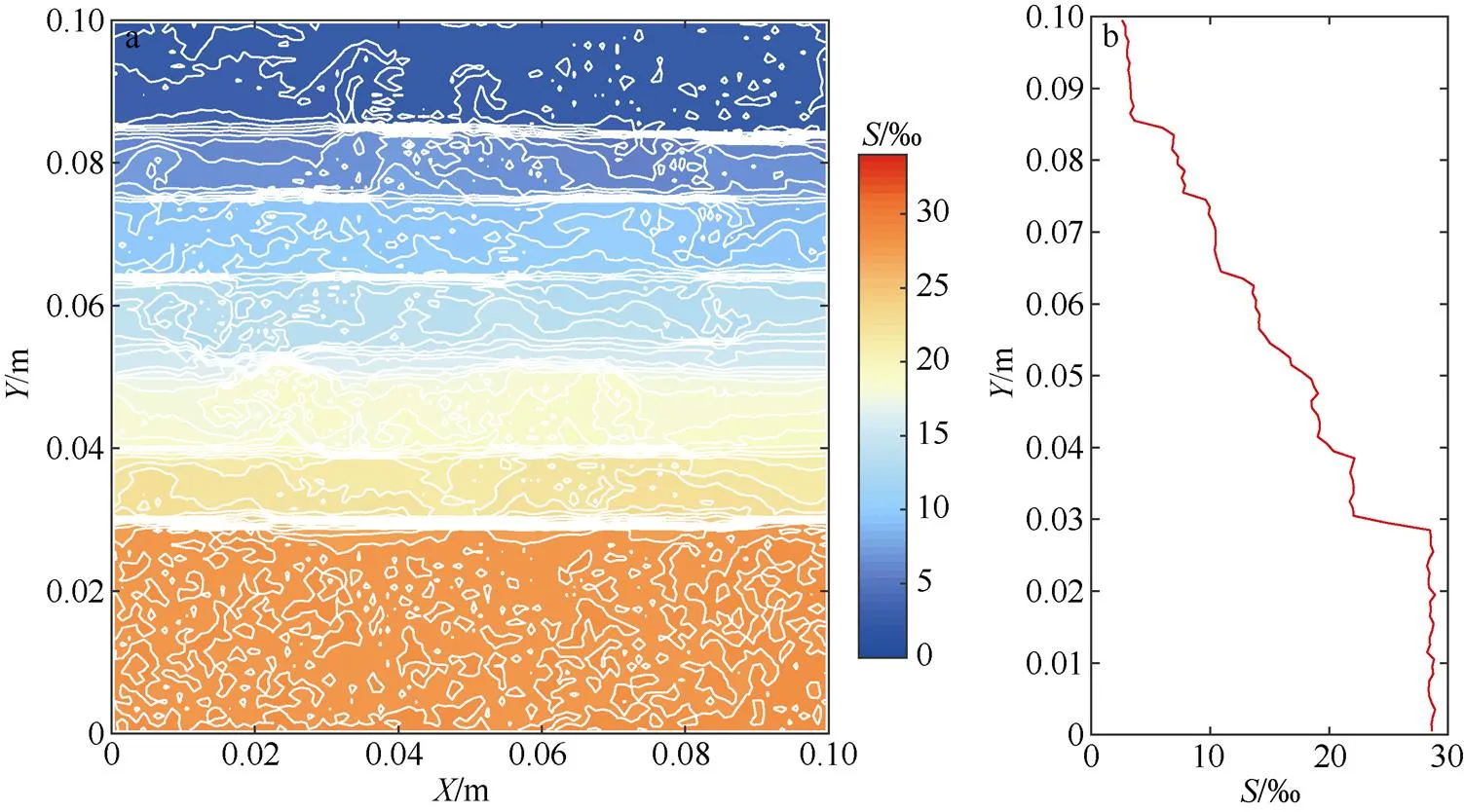
图9 情况④扩散对流模拟2.764h后盐度状态图

a. 等值线图; b. 曲线图

Fig. 9 Salinity distribution after 2.764 h in diffusive convection simulation of case 4: (a) contour plot, and (b) line plot

3 结论

本文对扩散对流现象进行了数值模拟, 模拟时采用线性层结的盐水系统, 底部加热, 顶部冷却。在扩散对流温盐台阶的演化过程中, 温度和盐度的变化趋势基本一致, 存在着温盐台阶的生成与合并。约在模拟开始的1h之前, 台阶的生成速率要大于台阶的合并速率, 表现为台阶数目的增多; 之后达到一个相对稳定的阶段, 接下来台阶结构不再生成, 只存在合并过程。约在1.5h之后, 次稳定层厚度逐渐减小, 直到消失, 在合并的过程中, 历时较长, 最终整个系统达到一个温度和盐度相对均匀稳定的状态, 形成一个大尺度的环流。

在整个温盐台阶结构的演变过程中, 温度和盐度曲线的变化趋势基本是一致的。对于流场中物质和能量的输运而言, 在扩散界面内部, 主要以分子扩散的形式输运物质, 以分子热传导的形式输运热量; 而在均匀的混合层内部主要以对流的形式输运物质和能量。

另外, 在不同热流密度情况下, 对扩散对流温盐台阶结构的演变过程进行了对比讨论, 分析了热流密度对温盐台阶结构形成的影响。模拟结果表明: 热流密度的变化主要是改变了温盐台阶结构的演变速率, 并不影响演变的趋势, 底部的加热和顶部的冷却都可以有效的加快其演变速率。

鲍征宇, 1989. 双扩散对流理论简介及国外研究现状[J]. 地质科技情报, 8(4): 35–42. BAO ZHENGYU, 1989. Brief double-diffusive convection theory and its recent development abroad[J]. Geological Science and Technology Information, 8(4): 35–42 (in Chinese with English abstract).

赖锡军, 2004. 温盐分层流的非结构网格数值模拟[D]. 南京: 河海大学. LAI XIJUN, 2004. Numerical simulation of stratified flows with combined temperature and salinity on unstructured grids[D]. Nanjing: Hohai University (in Chinese with English abstract).

卢玉华, 詹杰民, 2006. 三维方腔温盐双扩散的格子Boltzmann方法数值模拟[J]. 物理学报, 55(9): 4774–4782. LU YUHUA, ZHAN JIEMIN, 2006. Three-dimensional numerical simulation of thermosolutal convection in enclosures using lattice Boltzmann method[J]. Acta Physica Sinica, 55(9): 4774–4782 (in Chinese with English abstract).

屈玲, 2014. 海洋扩散对流温盐台阶机理及演化的研究[D]. 北京: 中国科学院大学. QU LING, 2014. The fundamental study of diffusive convection staircase and its evolution in the ocean[D]. Beijing: University of Chinese Academy of Sciences (in Chinese with English abstract).

万伟, 屈玲, 周生启, 2014. 双扩散对流中台阶结构的实验研究[J]. 力学学报, 46(2): 217–223. WAN WEI, QU LING, ZHOU SHENGQI, 2014. Laboratory studies on the staircase structure of double-diffusive convection[J]. Chinese Journal of Theoretical and Applied Mechanics, 46(2): 217–223 (in Chinese with English abstract).

邢元明, 杨磊, 管玉平, 2013. 海表扩散层中气体行为的分子动力学模拟[J]. 热带海洋学报, 32(2): 82–87. XING YUANMING, YANG LEI, GUAN YUPING, 2013. Molecular dynamics simulation of gas behaviors in seawater diffusive layer beneath the air-sea interface[J]. Journal of Tropical Oceanography, 32(2): 82–87 (in Chinese with English abstract).

詹杰民, 李毓湘, 2002. 温盐双扩散均衡场中的振荡现象[J]. 物理学报, 51(4): 828–834. ZHAN JIEMIN, LI YUXIANG, 2002. Oscillation phenomena in a thermohaline double-diffusive convection system[J]. Acta Physica Sinica, 51(4): 828–834 (in Chinese with English abstract).

郑珺婷, 詹杰民, 2002. 双扩散对流系统问题的研究进展[J]. 力学进展, 32(3): 415–424. ZHENG JUNTING, ZHAN JIEMIN, 2002. A review on double-diffusive convection[J]. Advances in Mechanics, 32(3): 415–424 (in Chinese with English abstract).

BEBIEVA Y, TIMMERMANS M L, 2016. An examination of double‐diffusive processes in a mesoscale eddy in the Arctic Ocean[J]. Journal of Geophysical Research: Oceans, 121(1): 457–475.

CARPENTER J R, SOMMER T, WÜEST A, 2012. Simulations of a double-diffusive interface in the diffusive convection regime[J]. Journal of Fluid Mechanics, 711: 411–436.

DURRAN D R, 1991. The third-order Adams-Bashforth method: An attractive alternative to leapfrog time differencing[J]. Monthly Weather Review, 119(3): 702–720.

FENG GUOLIN, CAO HONGXING, DONG WENJIE, et al, 2001. A new difference scheme with multi-time levels[J]. Chinese Physics, 10(11): 1004–1010.

GUO SHUANGXI, ZHOU SHENGQI, QU LING, et al, 2016. Laboratory experiments on diffusive convection layer thickness and its oceanographic implications[J]. Journal of Geophysical Research: Oceans, 121(10): 7517–7529.

GUTHRIE J D, FER I, MORISON J, 2015. Observational validation of the diffusive convection flux laws in the Amundsen Basin, Arctic Ocean[J]. Journal of Geophysical Research: Oceans, 120(12): 7880–7896.

GUTHRIE J D, FER I, MORISON J H, 2017. Thermohaline staircases in the Amundsen Basin: Possible disruption by shear and mixing[J]. Journal of Geophysical Research: Oceans, 122(10): 7767–7782.

HUPPERT H E, TURNER J S, 1972. Double-diffusive convection and its implications for the temperature and salinity structure of the ocean and Lake Vanda[J]. Journal of Physical Oceanography, 2(4): 456–461.

HUPPERT H E, LINDEN P F, 1979. On heating a stable salinity gradient from below[J]. Journal of Fluid Mechanics, 95(3): 431–464.

KELLEY D E, 1990. Fluxes through diffusive staircases: A new formulation[J]. Journal of Geophysical Research: Oceans, 95(C3): 3365–3371.

KELLEY D E, FERNANDO H J S, GARGETT A E, et al, 2003. The diffusive regime of double-diffusive convection[J]. Progress in Oceanography, 56(3–4): 461–481.

KIMURA S, NICHOLLS K W, VENABLES E, 2015. Estimation of ice shelf melt rate in the presence of a thermohaline staircase[J]. Journal of Physical Oceanography, 45(1): 133–148.

LEWIS W T, INCROPERA F P, VISKANTA R, 1982. Interferometric study of stable salinity gradients heated from below or cooled from above[J]. Journal of Fluid Mechanics, 116: 411–430.

MARMORINO G O, CALDWELL D R, 1976. Heat and salt transport through a diffusive thermohaline interface[J]. Deep Sea Research and Oceanographic Abstracts, 23(1): 59–67.

NEAL V T, NESHYBA S, DENNER W, 1969. Thermal stratification in the Arctic Ocean[J]. Science, 166(3903): 373–374.

SCHMITT R W, 1994. Double diffusion in oceanography[J]. Annual Review of Fluid Mechanics, 26: 255–285.

SHIBLEY N C, TIMMERMANS M L, CARPENTER J R, et al, 2017. Spatial variability of the Arctic Ocean's double‐diffusive staircase[J]. Journal of Geophysical Research: Oceans, 122(2): 980–994.

TURNER J S, 1965. The coupled turbulent transports of salt and and heat across a sharp density interface[J]. International Journal of Heat and Mass Transfer, 8(5): 759–767.

TURNER J S, STOMMEL H, 1964. A new case of convection in the presence of combined vertical salinity and temperature gradients[J]. Proceedings of the National Academy of Sciences of the United States of America, 52(1): 49–53.

TURNER J S, 1968. The behaviour of a stable salinity gradient heated from below[J]. Journal of Fluid Mechanics, 33(1): 183–200.

XIE LINGLING, LI MINGMING, LI MIN, 2015. Observational analysis of the double-diffusive convection in the deep Canada Basin[J]. Acta Oceanologica Sinica, 34(11): 71–79.

ZHOU SHENGQI, LU YUANZHENG, SONG XUELONG, et al, 2016. New layer thickness parameterization of diffusive convection in the ocean[J]. Dynamics of Atmospheres and Oceans, 73: 87–97.

Numerical simulation of diffusive convection staircase

XU Yan1, LIU Xiangquan1, 3, 4, SONG Rengang1, CEN Xianrong2, GUO Shuangxi2, ZHOU Shengqi2

1. College of Electronic, Communication and Physics, Shandong University of Science & Technology, Qingdao 266590, China; 2. State Key Laboratory of Tropical Oceanography (South China Sea Institute of Oceanology, Chinese Academy of Sciences), Guangzhou 510301, China; 3. State Key Laboratory of Integrated Optoelectronics, Institute of Semiconductors, Chinese Academy of Sciences, Beijing 100083, China; 4. College of Materials Science and Optoelectronic Technology, University of Chinese Academy of Sciences, Beijing 100049, China

Diffusive convection driven by temperature and salinity is a ubiquitous phenomenon in the mid and high latitudes of the ocean. Numerical simulation of diffusive convection can be used to study small-scale dynamic processes of the ocean. In this study, we analyze the formation mechanism of diffusive convection and establish a two-dimensional cavity model. The governing equation of the model is solved by the finite volume method, and the process of layering phenomenon is simulated numerically. The temporal evolution of temperature and salinity of the flow field is given, and the vortex structure of the velocity field is simulated. The processes of the formation and merging of diffusive convection staircases are analyzed, and a theoretical explanation for mass and energy transport processes is given. In addition, the diffusive convection under different heat flux density is discussed. It is found that the growth rate of diffusive convection staircases increases with the increase of heat flux density, and the cooling from the upper boundary plays an important role in accelerating its growth. The variation of heat flux density does not have a significant impact on the evolution of diffusive convection staircases.

diffusive convection; numerical simulation; salinity; temperature

2018-03-19;

2018-05-22. Editor: SUN Shujie

National Natural Science Foundation of China (11547037, 11604181, 41706029, 41776033); Natural Science Foundation of Guangdong Province (2016A030311042, 2016A030313155); Open Project Program of the State Key Laboratory of Tropical Oceanography (South China Sea Institute of Oceanology Chinese Academy of Sciences)(LTO1710)

P731.26

A

1009-5470(2019)01-0011-08

10.11978/2018028

2018-03-19；

2018-05-22。孙淑杰编辑

国家自然科学基金项目(11547037、11604181、41706029、41776033); 广东省自然科学基金项目(2016A030311042、2016A030313155); 热带海洋环境国家重点实验室(中国科学院南海海洋研究所)开放基金资助课题(LTO1710)

徐岩(1970—), 男, 山东省青岛市人, 教授, 从事凝聚态物理中的非线性现象和统计物理研究。E-mail: x1y5@163.com

岑显荣, 男, 博士, 主要从事海洋湍流混合的研究。E-mail: xrcen@scsio.ac.cn

CEN Xianrong. E-mail: xrcen@scsio.ac.cn