考虑灾后道路恢复情况下动态应急物资选址问题

孟燕萍， 申慢慢

(上海海事大学 物流研究中心，上海 201306)

0 引 言

自然灾害的发生，包括地震、洪涝、台风和沙尘暴等，往往伴随着人类生命和财产的巨大损失。2013年4月20日上午08：02，四川省雅安市芦山县发生7.0级地震，震中位于芦山县龙门乡，截止2013年5月1日，雅安地震共造成196人死亡，13 484人受伤(1 062人重伤)，失踪21人，累计受灾人数超过200万，累计经济损失高达1 693.58亿元[1]。

目前人类对自然灾害的发生只能预测，不能完全规避；故灾后救援应急等一系列活动就显得尤为重要。灾难发生后需要大量应急物资，包括救助伤员的医药用品、抢救被困人员的机械设备和满足灾民的日常生活用品等。灾后应急物资不同于一般物资，具有时效性、不确定性、弱经济性和非常规性等特征，而灾后道路恢复状况直接影响着救灾物资运输时效性。因此，考虑灾后道路恢复情况，不同道路恢复情况下对应不同应急救灾物资选址方案，可确保应急救灾物资有效、及时、合理的运送到受灾区，降低灾害造成的损失。

目前国内外学者在灾后应急物资选址问题上进行了深入研究。比如：S.L.HAKIMI[2-3]、C.TOREGAS等[4]、J.R.WEAVER等[5]分别针对应急选址问题将其分成3类来考虑，并对每类做出具体研究；J.DALAL等[6]通过建立飓风避难所的选址模型，进行算例分析，确定了避难所位置和容量，验证了模型实用性和有效性；C.G.RAWLS等[7]通过建立双层随机混合整数规划模型来研究应急物资分配选址问题；M.S.CANBOLAT等[8]通过建立随机模拟模型，确定了需求随机选址方案；S.DAVARI等[9]采用模拟退火算法求解选址问题，并提出了模糊最大覆盖问题；P.MURALI等[10]研究了应急物流选址距离因素和需求的不确定性，考虑容量限制的设施选址问题，建立了最大覆盖选址模型；王国利等[11]考虑了因意外事件导致设备瘫痪而造成的需求和供应不确定，并采用模糊理论方法建立了设施选址模型；詹沙磊等[12]考虑了多出救点、多受灾点和多应急物资的出救点选址问题，建立了多目标随机规划模型；张敏等[13]通过分析应急设施失效场景，建立最大覆盖选址模型来解决应急设施选址问题；陶莎等[14]考虑应急需求和物流网络均不确定情况，建立随机规划模型，并应用于应急物资配送点选址问题；陈洪凯[15]等研究公路受泥石流毁坏的程度及物资需求变化；P.MURALI等[10]考虑运输时间与需求的不确定性，建立了最大覆盖选址模型，并研究重大袭击事件发生后医疗设施选址问题。

这些学者多是以静态考虑设施选址问题，笔者则主要针对灾后不同时段道路恢复情况，对灾后应急物资选址进行了动态化研究。以最小化运输成本和灾民等待物资心理惩罚成本为目标，并权衡二次运输成本和灾民等待物资心理惩罚成本，提出多目标混合整数规划模型，基于不同道路恢复情况下选择最优应急物资选址方案，并以雅安地震为案例背景，验证了该模型的有效性和实用性。

1 问题分析

地震灾害发生后，需要及时向受灾区提供应急物资救援。但灾害发生后道路破坏及恢复情况不确定，使得灾后应急救灾物资运输难度加大，救灾情况更为复杂。根据灾后道路恢复情况合理分配应急物资选址，不仅能满足灾区对救援物资需求，而且能降低灾民等待物资的心理惩罚成本。

灾后道路恢复情况与救灾物资供给量密切相关，C.G.RAWLS等[7]以灾后72 h黄金救援时间为节点，给出了累计物资供应量，如图1。图1中：每12 h为一段，将灾后72 h分成了6段，每时段累计物资供应量不同，总体呈上升趋势。根据灾后道路恢复情况和累计物资供应量关系规律，可得出灾后道路恢复情况变化趋势，随着时间推移，灾后道路恢复情况呈上升趋势，如图2。动态化考虑应急物资选址是由灾后道路恢复情况所决定的。假设灾后某条被毁道路经修复后，某时段能正常通路，为满足最小化应急物资运输成本和灾民等待物资心理惩罚成本，需重新改变应急物资选址方案。同时，当选址方案变动，针对应急物资处理就会产生二次运输成本，即原应急物资选址点剩余物资需运送到新的应急物资选址点所产生的运输成本和新物资选址点设施建设固定成本。灾后道路恢复情况对灾民等待物资心理惩罚成本也有一定影响，新应急物资选址方案产生了二次运输成本，但能降低灾民等待物资心理惩罚成本。并非所有道路恢复情况变动都伴随着应急物资选址方案的变动，只有当灾民等待物资心理惩罚成本大于二次运输成本时，才会采取新的应急物资选址方案。

笔者考虑灾后道路恢复情况，以最小化应急物资运输成本和灾民等待物资心理惩罚成本为目标，建立多目标混合整数规划模型；并以雅安地震为例，实际分析了应急物资选址方案，验证了该模型的实用性和有效性。

图1 72 h物资累计供应量Fig. 1 72 h cumulative supply of materials

图2 灾后道路恢复程度Fig. 2 Degree of road rehabilitation after disaster

2 模型建立

2.1 符号定义

2.1.1 集 合

时段集合为T={1, 2, …,NT}，t∈T为其中一个时段；受灾点集合为D={1, 2, …,ND}，通过d∈D索引；供应点集合为S={1, 2, …,NS}，通过s∈S索引；道路集合为R={1, 2, …,NR}，通过r∈R索引。

2.1.2 参 数

2.1.3 决策变量

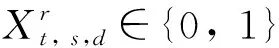
2.2 模 型

基于集合、参数和决策变量的定义，笔者给出了以最小化运输成本fc和灾民等待物资心理惩罚成本fpw为目标的模型，具体模型如式(1)～(11)：

Minimizef=fc+fpw

(1)

(2)

(3)

(4)

(5)

(6)

(7)

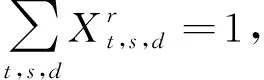
(8)

(9)

(10)

di≥0，i∈{1,2,…,15}

(11)

模型中：式(4)表示以灾后初始道路情况和道路恢复因子来量化灾后道路恢复情况；式(5)表示满足受灾点对受灾物资需求量，任意时段的救灾物资供应量须大于或等于需求量；式(6)表示受灾点缺货物资量是由总供应量减去总需求量决定的；式(7)表示供应点的总供应物资量不得超过供应点的物资容量；式(8)表示在任意时段内，只有一个供应点和一条道路满足受灾点的需求物资运输；式(9)表示任意时段内，总的物资运输量小于等于供应物资量；式(10)表示任意时段内物资运输量不为零；式(11)表示受灾点到供应点的道路距离大于零。

笔者基于以上分析，考虑到目标重要性和决策者的偏好问题，引入权重；为将目标函数的数量级差异统一化，引入统一量纲化处理。因此，为目标函数中运输成本和灾民等待物资心理惩罚成本赋予了相应的权重Wc和Ww，则目标函数模型如式(12)。

(12)

文中所建立的目标函数和约束条件考虑到灾民等待物资心理惩罚成本，考虑到受灾点需求物资被满足的约束条件，这样更符合实际。灾难应急物资更多考虑的是人道主义，人民生命安全需求大于一切。在实际救灾过程中，决策者宁愿花费高一点的成本也要满足灾民物资需求。笔者建立多目标混合整数规划模型，采用MATLAB求解，并得出最优解决方案。

3 算例分析

四川雅安受灾点根据道路距离芦山县的距离来判断道路恢复情况，以缩短运送物资距离为目的改变供应点，降低灾民等待物资心理惩罚成本。

笔者选取宝应县、芦山县和荥经县这3个受灾点；德阳市、成都市、眉山市、乐山市和资阳市这5供应点，供应点和受灾点经纬度如表1。根据实际经纬度的地理位置，为便于分析，转化成平面坐标(图3)。图3中：di表示供应点与受灾点的道路。统计分析供应点到受灾点的道路路线，灾害发生前这些道路处于完全通畅状态，见表2。

表1 受灾点和供应点的经纬度Table 1 Latitude and longitude of damage points and supply points

表2 供应点到受灾点的道路线Table 2 Road routes from supply points to disaster points

图3 供应点与受灾点之间道路线Fig. 3 Routes between supply points and disaster points

3.1 算例数据

表3 道路恢复状况下受灾点需求量Table 3 Demand of disaster-stricken areas under road restorationconditions

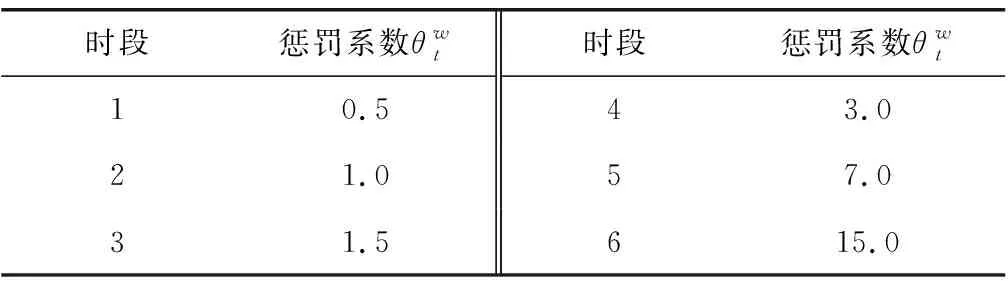
表4 各时段下灾民等待物资的心理惩罚系数Table 4 Psychological punishment coefficients of disaster victimswaiting for supplies at various time periods

表5 供应点的物资供应量Table 5 Material supply at supply points 万个

表6 受灾点到供应点的道路距离Table 6 The road distance from the disaster points to the supply points

表7 道路恢复等级Table 7 Road restoration level

3.2 算例分析

考虑到动态化分析道路恢复情况及应急物资选址问题，笔者根据实际情况假设了3种场景，并分析了算例结果。

3.2.1 场景1

灾害发生后，道路d4、d7、d8完全摧毁，在实际案例数据基础上，采用MATLAB算出最优解，得出最小运输成本fc=2 271.5和最小灾民等待物资心理惩罚成本fpw=780，确定了最佳供应点选址为德阳市、成都市和乐山市，使用道路为d1、d3、d14，如图4。

图4 供应点与受灾点之间道路线(场景1)Fig. 4 Road line between supply point and disaster point(scenario 1)

由图4可看出：在道路d4、d7、d8被摧毁的情况下，选出最优应急物资选址为d1、d3、d14，德阳市经过道路d1向受灾点宝应县供应救灾物资，成都市经过道路d3向受灾点芦山县供应救灾物资，乐山市经过道路d14向受灾点荥经县供应救灾物资。特别需要注意的是，由于处于道路完全摧毁状态，还没进入道路恢复阶段，故不存在二次运输成本。

3.2.2 场景2

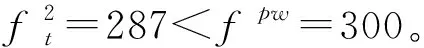
图5 供应点与受灾点之间道路线(场景2)Fig. 5 Road line between supply point and disaster point (scenario 2)

由图5可看出：d4、d7完全道路恢复，应急选址改变会产生二次运输成本，德阳市部分物资运输到成都市，资阳市部分物资运输到眉山市，降低了运输成本和灾民等待物资的心理惩罚成本。

3.2.3 场景3

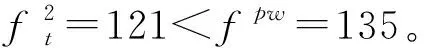
图6 供应点与受灾点之间道路线(场景3)Fig. 6 Road line between supply point and disaster point (scenario 3)

从图6可看出：d4、d7、d8道路完全恢复，应急选址由3个改变为2个(成都市和眉山市)，这其中产生了二次运输成本，德阳市部分物资运输到成都市，成都市、资阳市和乐山市的部分物资运输到眉山市。由结果来看，降低了运输成本和灾民等待物资的心理惩罚成本。

从以上3个场景分析得出：考虑道路恢复情况，根据路状及时改变应急物资供应更能节约救灾成本，提高灾民满意程度。在改变应急物资选址方面，会产生二次运输成本，这是由于原供应点与新供应点之间的运输，考虑道路质量高，因此单位道路运输成本大大下降(前文已给出单位二次物资运输成本)，权衡考虑灾民等待物资心理惩罚成本和二次运输成本，得出最优供应物资选址方案。

3.3 实验分析

基于以上结果，考虑模型中相关变量值和权重的影响，笔者设计了3种实验，并对实验进行分析。

3.3.1 实验1

从实验1得出：6个参数对运输成本fc和灾民等待物资心理惩罚成本fpw均有影响，随着需求量增加，导致运输成本增加和惩罚成本下降，这是因为满足灾民需求量，灾民满意度会提高，惩罚成本自然下降；供应量增加会带来运输成本和惩罚成本降低，因为供应量增加会出现单位运输成本较小的供应点，整体运输成本会降低；道路恢复因子逐渐增加，能够降低运输成本和惩罚成本，道路状况越好物资运送越快，因此会降低运输成本和惩罚成本；心理惩罚系数对运输成本影响不太明显，当心理惩罚系数越高时，惩罚成本也就越高；单位运输成本对惩罚成本影响较小，单位运输成本越高，则运输成本就越高；二次运输成本对运输成本和惩罚成本影响较明显，成正相关。

表8 6个参数的敏感性分析Table 8 Sensitivity analysis of six parameters

3.3.2 实验2

对运输成本fc和灾民等待物资心理惩罚成本fpw进行Pareto分析。实验中对权重Wc在(0,1)范围内以0.01的梯度变化进行松弛，Ww=1-Wc，对目标函数进行求解，绘制出Pareto分析图，如图7。

图7 运输成本和灾民等待物资心理惩罚成本Pareto图Fig. 7 Pareto diagram of transportation costs and the psychological penalty costs of disaster victims waiting for supplies

3.3.3 实验3

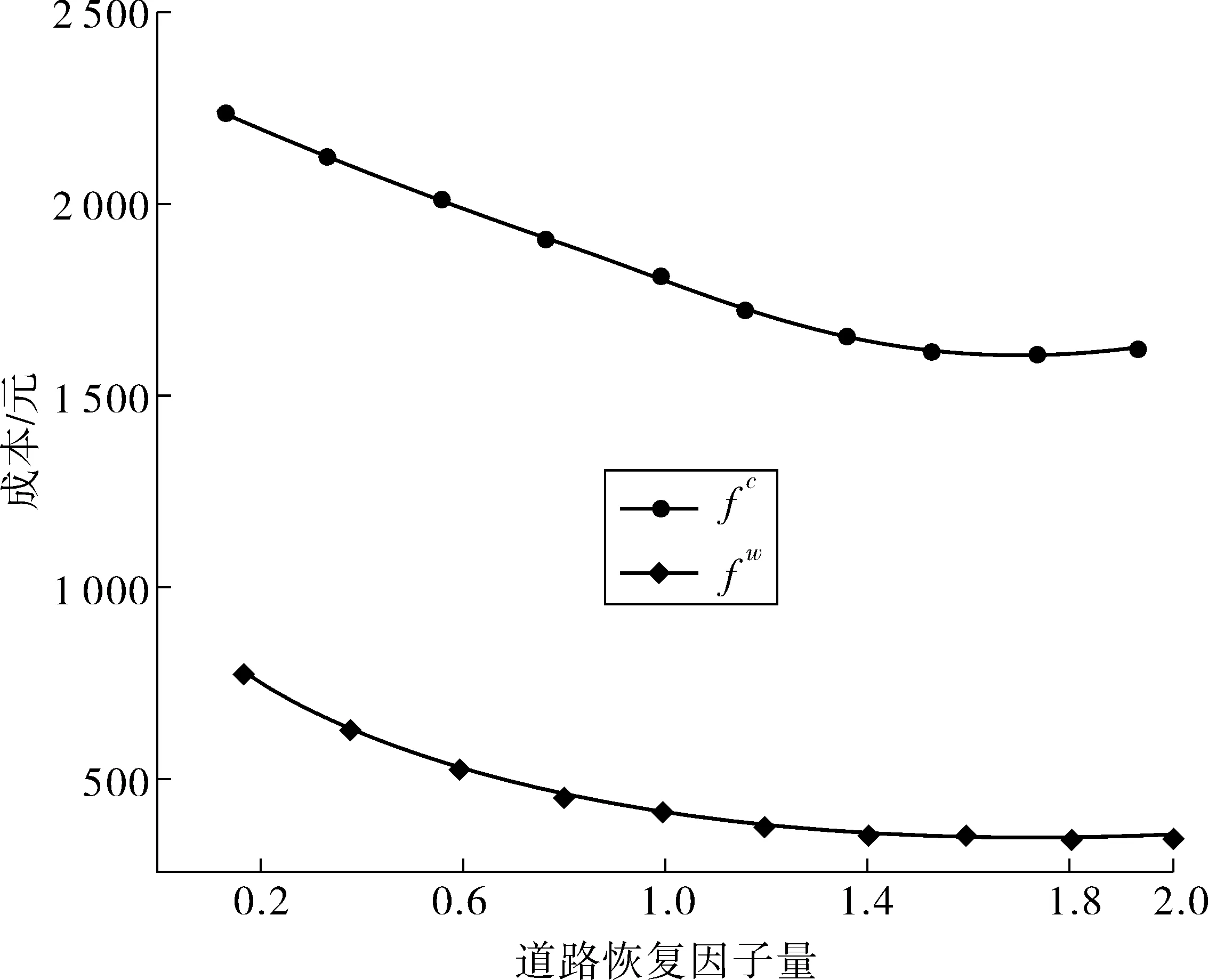
图8 道路恢复因子对实验结果的影响Fig. 8 Effect of road recovery factor on experiment results

通过图7、8可得出：通过Pareto分析，运输成本fc与灾民等待物资心理惩罚成本fpw两者成负相关，随着运输成本增加，灾民等待物资心理惩罚成本减少，考虑到实际灾难场景不难理解，运输成本提高，运输效率也会随之提高，从物资供应点运送物资到灾区花费的时间就少，应急物资能够快速运送到灾民手中，灾民等待物资的惩罚成本就会相应减少；道路恢复程度对实验结果均有影响，不同阶段下道路恢复程度不同，随着道路恢复因子数值增大，运输成本和灾民等待物资心理惩罚成本都会降低，其中惩罚成本的变化会更加明显。

4 结 论

笔者研究了灾后道路恢复情况下应急物资选址问题。以最小化物资运输成本和灾民等待物资心理惩罚成本为目标，建立多目标混合整数规划模型，并以雅安地震为实际案例验证模型的有效性。笔者根据道路恢复等级权衡灾民等待物资心理惩罚成本和二次运输成本，当惩罚成本大于二次运输成本就会改变选址方案，重新规划出最优方案。通过雅安地震的3个场景分析得出，道路恢复情况不同，物资选址方案也不同，考虑道路恢复情况，权衡二次运输成本和灾民等待物资心理惩罚成本有利于降低物资运输成本和灾民等待物资的心理惩罚成本，对实际灾后工作有很大帮助。

笔者通过研究3个实验得出的：① 在物资选址方面，考虑灾后道路恢复等级能够选出最佳的选址方案；权衡考虑灾民等待物资心理惩罚成本和二次运输成本更加符合实际，灾难发生，出于人道主义，灾民的利益大于一切，把灾民的利益和二次运输成本量化比较，不仅能够满足灾民，同时也降低经济成本；② 物资运输成本和灾民等待物资心理惩罚成本在一定范围内成负相关，当超过界限，两者之间的关系是正相关，因为当灾后道路完全恢复，灾民等待物资的心理惩罚成本几乎很小，这时物资运输成本也会因为路况和物资供应量而变得很小。