基于群层次分析法的雷达导引头抗干扰性能评估

臧翰林，李艳玲

(火箭军工程大学，陕西 西安 710025)

0 引言

近年来，雷达技术、体制得到不断提升，相应地，干扰装备和干扰技术也在不断升级换代，雷达干扰模式呈现出自适应、多元化等特点，雷达导引头面临着十分复杂的战场环境，存在很多不确定性因素，对其抗干扰性能进行有效地评估对于决策者的决策有重要的参考价值。由于实验成本昂贵，雷达导引头外场实测数据获取十分困难，仿真实验也不能够全面地反映雷达导引头的真实作战环境，使得通过实验直观评价雷达导引头抗干扰性能就不易实现。近年来，通过合适的评估方法对雷达导引头进行评估是一个普遍的思路。

目前常用的雷达导引头抗干扰性能评估方法有主成分分析法[1]、神经网络法[2]以及层次分析法等。主成分分析法的结果依赖于原始变量的结果；神经网络法虽然具有逼真的非线性的优势，但是对数据的准确性和数量要求较高，而雷达导引头数据的获得较难，难以进行有效的定量评估；层次分析法在实际应用中不需要复杂的对抗试验，可以节省成本，且具有定性和定量相结合的优势，是一种适合雷达导引头抗干扰性能评估的方法，但层次分析法依赖单个专家的评价结果，专家的主观判断、个人偏好对决策结果的影响很大。雷达导引头结构复杂，抗干扰性能指标具有多样化、不确定性的特点，考虑到领域内的专家知识结构具有方向性、不完备性特点，利用单个专家进行决策会导致决策结果片面化，很难得到准确、完备的评估结果。本文针对此问题，提出了基于群层次分析法(GAHP)的雷达导引头抗干扰性能评估方法。

1 雷达导引头抗干扰性能指标分析

指标的选取对于雷达导引头抗干扰性能评估具有十分重要的作用，简洁、全面的指标体系既能够降低评估难度，又能使评估结果更加可信。

雷达导引头抗干扰性能指标的选取主要有功率准则、信息准则、概率准则等，然而单一准则很难全面地反应导引头的抗干扰性能，因此本文结合不同的指标选取准则，分别从雷达固有抗干扰能力、抗压制式干扰能力和抗欺骗式干扰能力三个方面考虑，建立指标体系如图1所示。

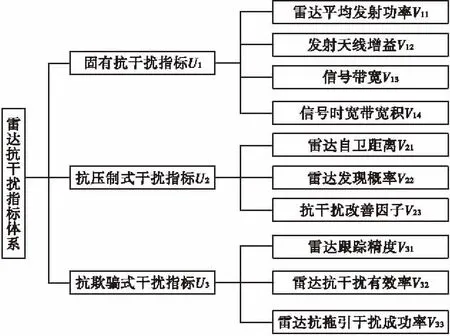
图1 雷达导引头抗干扰能力指标Fig.1 Anti-jamming capability index of radar seeker

1.1 抗压制式干扰能力指标

1)雷达自卫距离

雷达的自卫距离又称烧穿距离，是在受到压制式干扰时，雷达的最大作用距离，记：

(1)

可以看出雷达的自卫距离与雷达有效照射目标能量Ee成正比，与雷达在方位角上的波束宽度Δθs和俯仰角上的波束宽度Δαs成反比。

2)雷达发现概率Pd

雷达发现概率是指干扰信号的功率超过雷达能够正常监测时阈值的概率。当Pd达到对应型号雷达的发现概率阈值时，则能够监测目标，Pd的隶属度函数可表示为：

(2)

3)抗干扰改善因子EIF

EIF是一种用来衡量雷达导引头采用抗干扰措施后抗干扰能力的指标。抗干扰改善因子是指接收机在有无抗干扰措施的情况下，雷达系统输出的信干比之间的比值。表示如下：

(3)

式(3)中，(S/J)k表示采取抗干扰措施后的雷达输出信干比 ，(S/J)o表示未采取抗干扰措施雷达输出信号比。

1.2 抗欺骗式干扰能力指标

1)雷达跟踪精度

跟踪精度是跟踪雷达的主要性能指标，其隶属度函数可表示为：

(4)

2)雷达抗干扰有效率

雷达在面临欺骗式干扰的情况下，未受到欺骗的概率即为抗干扰有效率。

3)抗拖引干扰成功率PA-r

拖引干扰是指使雷达目标航迹产生误差，从而无法跟踪目标。距离拖引的成功率越高，则产生的误差越大，抗干扰性能越差。

2 基于群层次分析法综合评估模型

本文进行评估时，主要对群层次分析法的以下两个问题进行了创新：专家意见的表达方式和专家赋权问题。在评估过程中，专家的决策信息是评估结果是否符合事实的前提，目前，专家的决策信息大多是通过1～9标度法给出，但是考虑到专家知识、经验的不同，在专家打分时并非全部专家都可以给出确定的评价结果，可能产生犹豫不决的情况，因此本文用区间数表示专家决策信息的不确定性，提出将区间数[3]和1～9标度法相结合的思路，较好地融合不同专家的决策信息；在专家赋权问题上，赋权质量的好坏将直接影响着评估的结果，目前的方法主要有主观法[4]、客观法[5-7]和主客观组合法[7-8]等，这些方法要么过于复杂，要么真实度和客观度不够，本文针对上述两种专家意见表达方式分别采用基于决策信息一致性和灰度关联法给专家赋权，使评估结果更加合理和有效，具体的评估流程如图2所示。

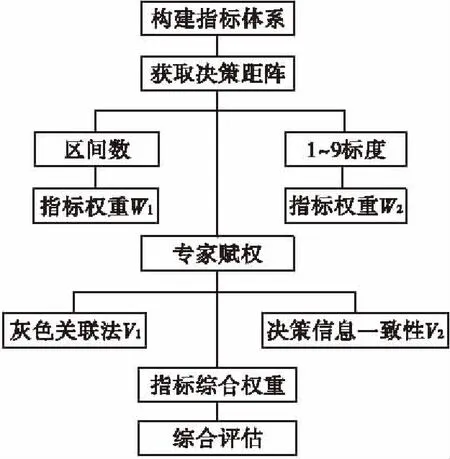
图2 群层次分析法评估流程图Fig.2 Group AHP evaluation flow chart

2.1 区间数和1～9标度法

如何更加合理地获得专家决策信息是评估的基础。1～9标度法是一种简单又实用的标度方法，专家通过两两比较的方法对指标的重要程度进行打分，构建决策矩阵，具体标度准则如表1所示。

表1 1～9标度表

利用区间数获取专家决策信息的原理类似于1～9标度法，不同的是在专家打分时采用区间数的形式来表示专家的不确定性。记a=[aL,aU]，b=[bL,bU]分别为两个区间数，则区间数间的运算规则如下：

1)a±b=[aL±bL,aU±bU]

2)ka=[kaL,kaU]

2.2 专家赋权

在评估过程中，由于各位专家研究方向和经验的不完全相同，加上专家自身的偏好等因素的影响，使得决策结果可能差异很大，所以如何合理地给专家赋权是群决策研究的重点。

本文针对两种专家决策信息获取方式分别采用基于灰色关联法和专家决策信息一致性的方法来确定专家的权重，有效地改善了以往专家赋权时偏主观性的缺点。

2.2.1灰色关联法

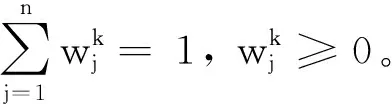
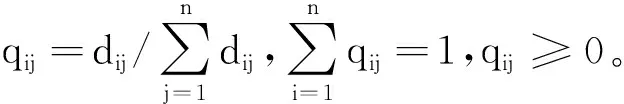
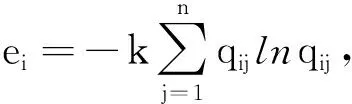
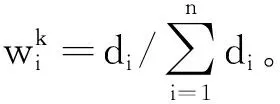
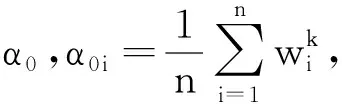
定义2.1 被比较序列与参考序列的灰色关联系数为

(5)

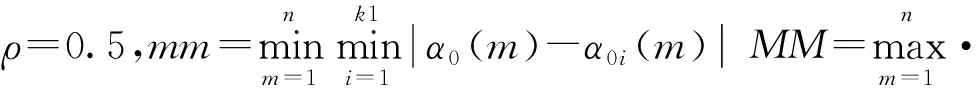
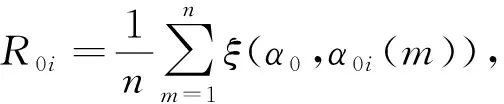
2.2.2基于专家决策信息的专家赋权

确定因素集，邀请K2名专家对每个指标按照确定数1～9标度法打分，得到判断矩阵Ak2。单独考虑每个专家给出的判断矩阵Ak2，求指标权重Wk2，具体如下：

1)判断矩阵Ak2中每行元素相乘，然后开n次方根得到

2)归一化后求得由专家Jk2得到的指标权重向量Wk2。

基于专家决策信息的一致性确定专家权重时，主要从专家决策结果和判断矩阵来考虑。用CR表示Ak的一致性，CR越小，则认为该专家的评判越合理，所以赋予该专家较高的权重。对于专家决策结果的一致性，可以比较由专家Jk与其他专家得到的指标权重的差值，差值越小，说明决策结果越趋向一致群体意见，则该专家权重应较高。定义专家Jk与由其他专家得到的指标权重差值为Dk，且

(6)

专家客观权重模型为：

(7)

引入Lagrange函数求解上述模型：

分别对vk和θ求导得到：

(8)

从而解得专家的客观权重：

(9)

进而得到专家客观权重向量V2。

2.3 指标赋权

由前面两种方法分别可以得到两组专家权重向量V1、V2，由指标权重向量Wk1、Wk2构成矩阵W1=(W1,W2,…,WK1)、W2=(W1,W2,…,WK2)，则两种方法分别得到的指标综合权重是G1=V1·W1T、G2=V2·W2T，则指标的组合权重为Q=0.5G1+0.5G2。

3 仿真算例

首先邀请6位相关领域的专家对雷达固有抗干扰能力指标进行评估打分，由于各专家的知识水平及经验等方面存在差异，有三位专家能够给出确定评估信息，另外三位专家存在犹豫不决的情况，因此在获取专家决策信息时前三位专家采用区间数法，后三位专家采用1～9标度法，决策矩阵如下所示：

3.1 专家赋权

针对不同的专家意见获取方式需要采用不同的方法确定专家权重，本文针对上述两种方法分别了采用基于灰色关联法和专家决策信息一致性的方法来确定专家权重。

3.1.1灰色关联法

针对区间数决策矩阵，根据2.2.1中方法可以得到由各个专家得到的指标权重向量作为被比较序列：

W11=α1=(0.329 6,0.329 6,0.134 1,0.206 8)，

W12=α2=(0.135 6,0.205 7,0.334 2,0.324 5)，

W13=α3=(0.217 2,0.177 5,0.255 1,0.350 2)。

从而可以得到专家群体参考序列为：

α0=(0.227 5,0.237 6,0.241 1,0.293 8)

根据定义2.1，则各专家与理想方案的关联系数为：

ξ(α0,α01)=(0.410 0,0.438 5,0.397 5,0.454 1)，
ξ(α0,α02)=(0.438 8,0.747 1,0.440 6,0.757 7)，
ξ(α0,α03)=(1,0.561 6,0.945 2,0.580 5)。

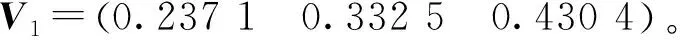
3.1.2专家决策信息一致性

根据确定数决策矩阵，利用2.2.2中提到的方法计算后三位专家的权重，具体方法如下：

步骤1 计算由每个专家得到的指标权重：

W21=(0.388 9,0.388 9,0.068 7,0.153 5)，
W22=(0.467 3,0.277 2,0.016 1,0.095 4)，
W23=(0.072 6,0.473 0,0.170 0,0.284 4)。

步骤2 进行一致性检验。

在计算指标权重Wk的同时可以得到判断矩阵的最大特征值分别是λ1=4.043 5，λ2=4.031，λ3=4.051 1。

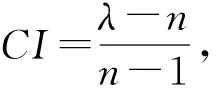
步骤3 计算每个专家的权重vk。

首先计算Dk。根据公式(6)计算得到D1=0.355 88，D2=0.528 78D2=0.528 78，D3=0.747 74。利用公式(9)求得专家的权重向量V2=(0.460 1 0.316 7 0.223 2)。

3.2 综合评估

由前面可以得到的专家权重向量V1、V2和由指标权重向量W1k、W2k构成的矩阵W1=(W1,W2,…,W1K)、W2=(W1,W2,…,W2K)，按照2.3节中计算方法可得到由两种方法分别确定的指标综合权重分别为G1=(0.343 1, 0.372 3, 0.099 7, 0.164 9)，G2=(0.283 1, 0.325 5, 0.181 3, 0.210 1)。则组合权重为Q=(0.313 1 0.348 9 0.140 5 0.187 5)。

采用本文与文献[9]提出的层次分析法求解的指标权重如表2所示，两种方法得到的指标权重排序一致，但是采用本文方法得到的指标权重分散性较强，能够更好地区分属性的重要程度，体现了模型的先进性和合理性。

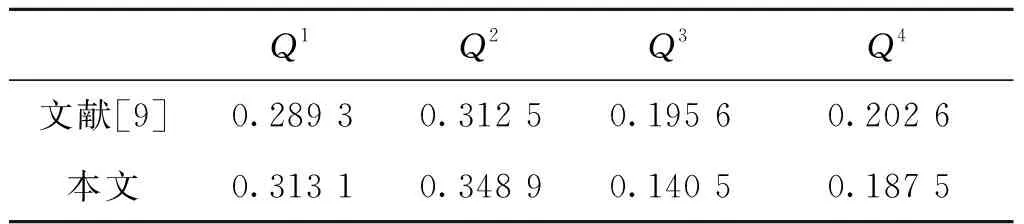
表2 两种方法得到的指标权重

雷达指标数据的获取主要是通过文献[10]和仿真计算得到。由于本文的重点是对传统的层次分析法进行改进，因此本文雷达导引头的指标数据直接引用文献[10]中的数据，处理后的数据如表3所示。

根据三种型号雷达的指标数据和指标权重，通过线性加权的计算方法得到的评估值对应PAC-1、SA-10、响尾蛇三种型号雷达分别为0.461 2，0.497 2，0.146 4。

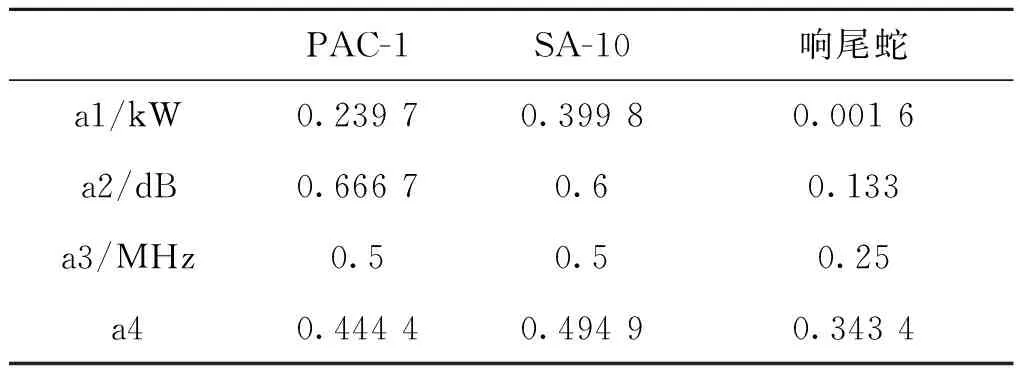
表3 模糊处理后的雷达数据

对于雷达抗压制式干扰性能和抗欺骗式干扰性能，可按照相同的步骤进行评估，分别给U2、U2、U3分配权重为(0.4， 0.3 ，0.3)，则按照线性加权的方法可算得三种型号雷达的最终评估值分别为0.531 4,0.506 9,0.223 4。从定量评估结果来看，PAC-1雷达的抗干扰性能比SA-10好，响尾蛇雷达的抗干扰性能最差。

4 结论

本文提出了基于群层次分析法的雷达导引头抗干扰性能评估。该方法将群决策和层次分析法结合，并且改进了传统单一的专家决策信息获取方式，采用了1～9标度和区间数相结合的方法来融合专家意见，并分别基于专家决策信息一致性和灰色关联法给专家赋权，使专家意见的集结更加具有客观性。通过实例验证，与传统的方法相比，利用该方法能够更加分散地表现指标相对重要程度，从而降低评估结果的模糊性，证明了模型具有先进性和实用价值。