基于Euler变换的非圆信号稀疏重构阵列测向方法

谭伟杰，冯西安，张肖璞

(西北工业大学航海学院，陕西 西安 710072)

0 引言

波达方位估计是阵列信号处理中的重要研究内容，已经广泛应用于雷达、声呐、通信、导航、射电天文、地震探测以及医学等各个领域中[1]。而低信噪比，少快拍条件下的波达方位估计一直是阵列信号处理中的一个难点。传统的信号处理算法大多只利用了信号的二阶相关统计信息，而非圆信号处理算法则同时利用信号的二阶相关和共轭相关统计信息，提高了信息利用率，所以利用信号的非圆特性来提高方位估计在该条件下的性能是一个有效的途径。在水下通信中最常用的调制方式一般采用二进制移相键控(Binary Phase Shift Keying，BPSK)[2]，该调制信号是一种典型的非圆信号，可以利用其椭圆协方差矩阵不为零的特征，增加接收矩阵数据维数，扩展阵列孔径，从而提高估计精度和解决欠定条件下的估计问题。1998年，Galy首次提出将非圆信号特征与阵列信号处理相结合，提出了非圆MUSIC (Non-circular MUSIC，NC-MUSIC) 来估计非圆信号的目标方位，并详细研究了非圆信号的特征[3]。2001年，Charge等人提出了非圆求根MUSIC (Non-Circular Root MUSIC, NC-Root-MUSIC)，用多项式求根代替NC-MUSIC中的谱峰搜索，大大降低了计算量[4-5]。2003年，Zoubir等人提出了非圆ESPRIT(Non-Circular ESPRIT， NC-ESPRIT)，在低信噪比情况下优于ESPRIT，并且能够解决欠定条件下的目标方位估计问题[6]。2004年，Tayem等利用阵列接收信号及其部分共轭信息，构造出具有旋转不变结构的两个均匀线列阵，提出了共轭ESPRIT(Conjugate ESPRIT，C-ESPRIT)[7]。这些算法均是在复数域进行的，计算量较传统子空间方法大。同年，Haardt等将空间平滑技术，将酉ESPRIT算法扩展到非圆信号的测向问题中，提出了非圆酉ESPRIT(Non-Circular Unitary ESPRIT， NC-U-ESPRIT)[8]。汪晋宽等人提出一种共轭酉ESPRIT (Conjugate Unitary ESPRIT，CU-ESPRIT)[9]，该方法构造了一个具有2M—1个阵元的虚拟阵列，提高了目标估计的个数。这些算法利用酉变换(Unitary Transformation)将复运算转换为实运算，在提高分辨率的同时，来降低计算量。郑春弟提出了应用Euler变换的实值MUSIC类和ESPRIT类非圆信号DOA估计算法[10-11]，这类算法利用了信号的非圆特性，通过欧拉变换构造出阵列接收数据的正弦部分和余弦部分，从而将复数运算转换为实数运算，该方法利用非圆信号的特征将数据转换为实数运算，使得计算量大为降低，并且通过数据拼接提高了虚拟孔径，提升了估计性能。

基于非圆信号特征的子空间类方法，虽然利用了非圆信号的特征，扩展了阵列孔径，但是在小快拍，低信噪比情况下性能大打折扣，尤其是在相干情况下，需要通过平滑处理来提高分辨性能，其代价是牺牲阵列孔径。本文针对在小快拍，低信噪比情况下，基于非圆信号特征的子空间类方法分辨精度不高的问题，结合Euler变换与稀疏信号重构方法，提出了基于Euler变换的非圆信号稀疏重构阵列测向方法。

1 非圆信号阵列模型

考虑包含有M个阵元的均匀线性阵列。假设有K个窄带目标信号分别从远场θ1,θ2,…,θK方位照射到阵列。这里假定目标信号为非圆信号，信号可以是相关的，甚至是相干的。不同时间快拍的信号表示为sk(t)，t=1,2,…,T，k=1,2,…,K。那么该阵列接收的信号矢量可以表示为：

(1)

2 基于Euler变换的实值稀疏重构DOA算法

2.1 欧拉数据变换

传统上的实值化通常采用Unitary变换[12]，该变换是将复数数据转化为实数数据的一个重要方法。与之前不同，这里利用非圆信号的特点通过欧拉变换来将数据从复数数据转化为实数数据，从而扩展阵列的虚拟孔径。

xR=(x(t)+x*(t))/2

(2)

根据欧拉公式，这里不考虑信号附加相位的影响，那么第i个阵元上的接收信号可以表示为：

(3)

该式可以改写为：

xR(t)=AR(θ)s(t)+nR(t)

(4)

式(4)中，

AR(θ)∈M×K,nR=Re(n)，Re(·)表示取实部。

进一步可以得到

xI(t)=(x(t)-x*(t))/2j

(5)

同理，

(6)

该式可以写为：

xI(t)=AI(θ)s(t)+nI(t)

(7)

式(7)中，

AI(θ)∈M×K,nI=Im(n)，Im(·)表示取实部。

令，

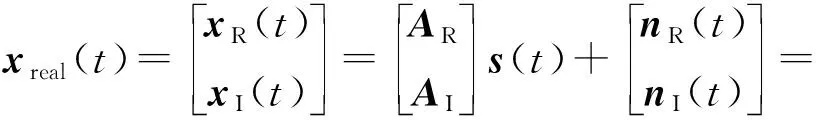
(8)

式(8)中，Areal(θ)∈2M×K，AR(θ)∈M×K，AI(θ)∈M×K，nR∈M×1，nI∈M×1。

可以看出，利用非圆信号的特点后，通过欧拉公式得到一个新的维数为2M×1的等价阵列，相当于扩展了阵列孔径。此时数据转化为实数运算，已有的方法是在此基础上基于子空间类的方法，如Euler MUSIC、Euler ESPRIT，虽然也利用了非圆特性，但不能直接处理相干信号，这里采用稀疏表示的方法来求解，可以在小快拍、低信噪比下以及相干源情况下得到更好的分辨效果。考虑到多个时间快拍，公式(8)表示为矩阵形式：

Xr=ArealS+Nr

其中，Xr=[xreal(1),…,xreal(T)]，S,Nr采用和Xr同样的构造方式。

2.2 基于实值稀疏信号重构的DOA估计

定义一个过完备的导向矢量字典

Φ=[a(θ1),a(θ2),…,a(θQ)]∈C2M×Q

(9)

其中，areal(θl)=[1,cos(2πd2/λsin(θl)),…,cos(2πdM/λsin(θl)),0,sin(2πd2/λsin(θl)),…,sin(2πdM/λsin(θl))]是所有可能出现目标的方向阵列流行向量。Areal⊂Φ，Q为离散化的网格数，Q≫max(M,K)。基于这种定义，Φ是被预先确定并不依赖于真实方位的过完备阵列流行矩阵。假设真实目标的方位(θ1，θ2，…，θk)都包含于(或者非常接近于)过完备词典(θ1,θ2,…,θQ)中，式(8)的阵列信号处理模型可以改写为:

xreal(t)=Φs(t)+n(t)

(10)

式(10)中，s(t)=[s1(t),…,sQ(t)]T∈CQ×1是阵列接收到的信号的扩展，只有当θq=θk时，sq(t)=sk(t)，其他情况下sq(t)均为0。由此可见，式(10)的信号模型是稀疏的，此时目标的方位估计就转变为对s(t)的非零位置估计的问题。式(10)是一个典型欠定线性方程，恢复s(t)是一个典型的稀疏信号重构问题。由Donoho等的压缩感知理论，在无噪声情况及Φ满足一定条件下，s(t)可以通过l0范数最小化完全重构：

(11)

在有噪声情况下，s(t)可以通过l0范数最小化完全重构：

(12)

但是上式是一个NP难问题，是非凸的，现有的优化算法很难有效求解。可以通过松弛条件将采用l1范数来逼近l0范数，此时问题转化为：

(13)

式(13)中，ε是与噪声水平相关的参数。该问题可以采用内点法来求解。但是当快拍数很大时，求解上述问题的计算维度将大大增加，为了降低运算复杂度，减小计算量，采用奇异值分解来降低数据处理维度。

2.3 基于奇异值分解的实值稀疏信号重构DOA估计

对Xr进行奇异值分解[13]

(14)

这里Us∈C2M×K，Vs∈CN×K对应K个最大奇异值对应的奇异值特征向量，为得出维度减低的2M×K维信号空间，引入了新的矩阵

(15)

式(15)中，SSV=SVs，NSV=NrVs。

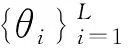
(16)

(17)

3 仿真与分析

本节对提出的基于Euler变换的非圆信号稀疏重构阵列测向方法进行数值仿真。在非相干非圆信号和相干非圆信号情况下，将本文提出的方法和MUSIC、NC-MUSIC方法测向性能进行比较。

仿真中，阵列是阵元数目为8，阵元间距为半波长的均匀线列阵。目标的信号波形为非圆信号，采用BPSK 调制信号，噪声为加性高斯白噪声。

实验1 非相干源下的测向能力比较

两个非相干目标源的方位为 [-2°,2°]，信噪比为0 dB，快拍数为20。图1 是在信噪比为0 dB情况下稀疏重构方法以及MUSIC 和NC-MUSIC方法的空间谱图。图2是信噪比从-10 dB到25 dB变化时，RMSE与信噪比关系曲线，每个曲线通过200次蒙特卡洛实验得到。

图1 非相干目标的邻近目标归一化空间谱比较Fig.1 Comparison of normalized spatial spectra of uncorrelated closely targets

图2 非相干目标条件下RMSE与SNR的关系曲线Fig.2 RMSE versus SNR for uncorrelated targets

由图1可知，采用稀疏重构的方法可以在低信噪比条件下分辨空间相近目标，而传统的MUSIC方法和NC-MUSIC方法在低信噪比条件下不具有分辨近空间目标的能力，主要原因在于一方面是非圆特性的利用提高了阵列孔径，稀疏重构方法能够在测量数较少的情况下获得较好的信号重构，从而获得较好的目标测向性能。由图2可以看出，在低信噪比情况下，基于欧拉变换的稀疏重构方位估计方法的最小均方误差远远小于传统的NC-MUSIC和MUSIC，表明了其在低信噪比、小快拍条件下的优越性。

实验2 非相干源下的测向能力比较

两个相干目标源的方位为 [-4°,4°]，信噪比为0 dB，快拍数为20。图3是在信噪比为0 dB情况下稀疏重构方法以及MUSIC 和NC-MUSIC方法的空间谱图。图4是信噪比从-10 dB到25 dB变化时，每个信噪比做200次蒙特卡洛实验得到的最小均方误差和信噪比的关系图。

由图3可知，采用稀疏重构的方法可以在低信噪比条件下分辨相干非圆信号近空间目标，而传统的MUSIC方法和NC-MUSIC方法不具有在相干条件下的分辨目标的能力，其原因在于子空间类方法需要利用协方差矩阵，目标的相干性使得协方差矩阵降秩，无法直接区分出信号子空间和噪声子空间，必须使用空间平滑预处理才能分辨出信号。由图4可以看出，基于欧拉变换的稀疏DOA估计方法随着信噪比的增加均方根误差逐渐减小，其具有相干信号分辨的能力。

实验3 欠定条件下的目标方位估计性能

考虑阵元数目为4，5个相干非圆信号，目标的方位分别为[-40°,-20°,0°,20°,40°]，信噪比为0 dB，快拍数为20，验证所提方法在欠定条件下目标方位估计的性能。 图5比较了在相干非圆信号情况下所提方法和NC-MUSIC方法的空间谱。

图3 邻近相干目标的归一化空间谱比较Fig.3 Comparison of normalized spatial spectra of coherent closely targets

图4 相干目标条件下RMSE与SNR的关系曲线Fig.4 RMSE versus SNR for coherent targets

图5 欠定条件下多个非圆目标的不同方法归一化功率谱比较Fig.5 Comparison of normalized spatial spectra of multiple coherent closely targets

由图5可以看出，在非圆信号目标个数大于阵元个数的情况下，NC-MUSIC和本文提出的方法都能分辨出目标，但是本文提出的方法谱线峰值更明显，具有更高的分辨能力，性能更优，说明其在欠定条件下具有高分辨性能。

4 结论

本文提出了基于Euler变换的非圆信号稀疏重构阵列测向方法。该方法利用非圆信号的特征，采用Euler变换将复数据转化为实数据，通过数据拼接来扩展阵列孔径，采用奇异值分解来降低数据维度，利用目标方位信息的空域稀疏性，通过离散化空间方位网格来构建实数域的空域字典集，将目标方位估计问题转换为一稀疏信号重构问题，最终通过实值稀疏信号重构方法来估计目标方位。 数值仿真验证表明，在低信噪比以及少快拍情况下，无论是对于非相干信号或者相干信号，与传统方法相比，所提方法皆表现出良好的估计精度，且该方法可以应用于欠定情况下非圆信号的目标方位估计。该方法的不足之处是所提方法是在精确补偿传输延迟而产生的复相移的前提下，下一步将考虑联合估计复相移和目标方位。