融合帧间相关性的能量检测方法
曾晓宇,矫文成,孙慧贤
(陆军工程大学石家庄校区,河北 石家庄 050003)
0 引言
由于当前的固定频谱分配策略,频谱资源利用率十分低下,如何高效提高频谱利用率的问题受到人们广泛关注。
为解决上述问题,人们提出了认知无线电的概念[1]。认知无线电的核心和基础是频谱感知技术[2],频谱感知主要的功能是探测可用频率或频谱空洞。同时,频谱感知还应该具有实时探测授权用户状态的能力,从而避免非授权用户干扰主用户。
常用的频谱感知算法有能量检测[3],匹配滤波检测[4]和循环特征量检测[5]三种。由于能量检测实现简单并且不需要任何的信号先验信息,所以能量检测被广泛应用于认知无线电系统中。但是当信号的信噪比降低时,能量检测的检测性能会降低。同时,真实环境中的噪声不确定性,也会恶化能量检测的检测性能。为了解决该问题,文献[6]提出了双门限能量检测方法,但是在单用户检测下的检测性能仍不够理想。文献[7]提出了多个用户协同感知的方法,能有效提高检测性能,但要求用户间具有较高的信息的互传能力。文献[8]将本地判决分为硬判决与软判决,仅当软判决时才使用协同感知的方法,降低了对多用户间信息吞吐量的要求。文献[9]利用信道占用的马尔科夫性,提出了一种动态双门限检测策略,在增加频谱感知精度的同时还降低了认知用户的感知时间。
上述文献中对能量检测的研究,对检测性能的提升都要基于多用户下的协作感知,对单一用户的检测性能无法产生实质上的提升。本文着眼于单体用户,针对低信噪比下,不确定噪声降低检测性能的问题,提出了一种融合帧间相关性的能量检测方法。
1 能量检测
1.1 能量检测模型
能量检测是一种常用的简单有效的频谱感知方法,它通过计算接收的信号能量,与预设门限值进行比较,来判断信道状态。
频谱感知是一个二元假设检验问题,其表达式为:
(1)
式(1)中,H0表示主用户不存在,信道处于空闲状态;H1表示主用户存在,信道处于占用状态;y(k)表示主用户实际接收到的信号;n(k)表示主用户接收到的噪声信号;s(k)表示主用户接收到的主用户信号。
检验统计量为:
(2)
式(2)中,T表示接收到的信号能量;N表示检测时信号的抽样数目。
在AWGN信道下,检验统计量服从以下分布:
(3)
当采样点数N足够大时,根据中心极限定理,卡方分布可以近似为高斯分布。因此,检验统计量的分布形式改变为:
(4)
1.2 单门限判决
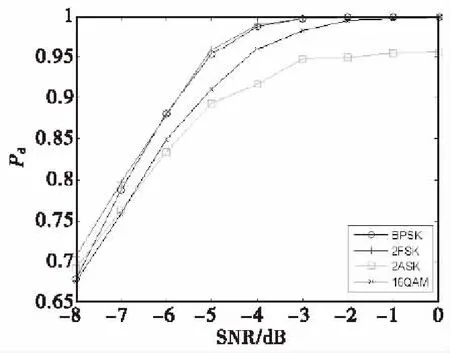
传统单门限判决会设置一个门限值Vth:当检验统计量T>Vth时,判定主用户存在,信道处于占用状态;当T 检测概率与虚警概率是评估检测性能的两个重要参数,在判决门限Vth给定的情况下,其计算公式为: (5) (6) 式(5)、式(6)中,Pd表示检测概率,即主用户存在时,判决结果为信道占用的概率;Pf表示虚警概率,即主用户不存在时,判决结果为信道占用的概率。 根据恒虚警概率的原则,可以反推得到判决门限值: (7) 单门限判决情况下,假设了接收端的的噪声功率是理想恒定不变的。然而,在真实环境中的噪声除了包括高斯白噪声之外,可能还包括一些其他干扰噪声,噪声功率是随着时间和相对位置在一定范围内变化的,即噪声存在不确定性[10]。 噪声不确定性区间的模型为: (8) 噪声的不确定性会恶化能量检测的检测性能。图1(a)显示了固定Pf=0.1时,Pd随着SNR的变化曲线。可以看出在SNR≤-2 dB时,噪声的不确定性的存在会明显降低检测概率。图1(b)显示了固定SNR=-6 dB时,Pd随Pf的变化曲线。可以看出在同等Pf下,噪声不确定时的检测概率,远低于理想噪声下的检测概率。 图1 噪声不确定性对能量检测的影响Fig.1 Influence of noise uncertainty on energy detection 由于噪声不确定性的存在会恶化能量检测性能的,为了提升检测概率,需要引进额外的参数来辅助判决。本文通过分析不同帧接收信号之间的相关性,辅助能量检测进行判决,以提高在噪声不确定下的检测性能。 相关检测是基于信号和噪声的统计特性进行检测的一门技术,通过计算信号间的相关函数来进行相似度判定。由于不同时刻的信号之间在频率、相位、波形以及调制方式上会具有一定的人为相似性,而不同时刻的噪声是独立随机的,所以统计上信号间相关函数的峰值会大于噪声间相关函数的峰值。这一特性即使在噪声存在不确定性时也存在,所以可以通过相关函数来辅助判决,以提高检测概率。 两个信号间的相关函数的定义为[11]: (9) 式(9)中,y1和y2分别为两个不同时刻的接收信号。 选取统计量为max{R(x)},噪声不确定度上界A=2,信噪比SNR=-6,以主用户采用BPSK调制为例。图2给出了通过10 000次蒙特卡罗仿真得到的统计量的分布关系,其中,横坐标参数Rmax代表统计量max{R(x)}的值,纵坐标number代表取得某max{R(x)}个数,曲线为仿真数据拟合的正态曲线。图2(a)为主用户存在时max{R(x)}的分布,图2(b)为主用户不存在时max{R(x)}分布。对比仿真数据与拟合曲线,两种情况下的仿真数据都近似于正态分布,但主用户存在时分布的均值(约100)要明显大于主用户不存在时的均值约(75)。说明使用相关函数峰值的方法具有可行性。 图2 相关统计量的分布Fig.2 Distribution of related statistics 图3所示为融合帧间相关的能量检测的判决方案。其中t1时刻是t2时刻之前并且判决结果为主用户存在的某时刻,融合判决采用or准则。 图3 融合帧间相关的能量检测Fig.3 Energy detection fused with interframe correlation 方法实现步骤流程如图4所示,由于使用的是or融合准则,考虑到降低复杂度与计算量的问题,采用顺序逻辑流程:先直接进行能量检测,当判决结果为主用户不存在时,再融合帧间相关信息进行结果修正。 在已经获得环境参数情况下,根据需求的虚警概率,利用式(7)可以得到能量检测量的门限值Vth,利用图2(b)中主用户不存在时相关统计量的分布规律,可以得到相关检测量的门限值λ。当max{R(x)}>λ或T>Vth时,判定主用户存在;当max{R(x)}<λ且T 图4 融合帧间相关的能量检测的步骤流程Fig.4 Step flow of energy detection fused with interframe correlation 为了验证融合帧间相关性的能量检测算法性能,分别做了3组实验。待检测信号BPSK、2FSK、2ASK与16QAM信号,码元速率为20 MB/s,载波频率fc为80 MHz(2FSK信号载波fc1=80 MHz,fc2=40 MHz)。 图5为考虑噪声不确定度存在的情况(不确定性上限A=1),融合帧间相关性的能量检测方法和能量检测方法检测概率Pd与信噪比SNR的关系。待检测信号为BPSK信号,假设虚警概率分别为0.025,0.05和0.1。进行5 000次蒙特卡罗仿真随机仿真,从图中可以看出,虚警概率为0.1时,直接进行能量检测,当信噪比下降到-4.7 dB以下就不能满足检测概率90%以上;而融合帧间相关性后,在信噪比为不低于-5.7 dB时,仍具有90%以上的检测概率。通过对比,融合帧间相关性的能量检测相较于直接能量检测,检测概率有了一定的提高。 图5 融合帧间相关性的能量检测和能量检测在不同虚警概率下的检测概率对比Fig.5 Comparison of detection probability of energy detection and energy detection fused with interframe correlation under different false alarm probabilities 图6对比了本文方法与文献[7]中双门限协作感知方法的性能。选取信号为BPSK信号,固定虚警概率为0.01。从图中可以看出,在用户数同为1时,本文方法的检测概率要明显高于文献[7]方法的检测概率;本文方法在用户数为1时的检测概率接近文献[7]方法在用户数为2时的检测概率,但明显低于文献[7]方法在用户数为3时的检测概率。说明本文方法在不增加感知用户数量时,能达到提高检测概率的目的,但检测概率提升的程度不及直接增加感知用户数量。 图6 融合帧间相关性的能量检测和双门限能量检测概率对比Fig.6 Comparison of detection probability of energy detection fused with interframe correlation and double-threshold energy detection 图7展示了融合帧间相关性的能量检测对不同调制信号的检测概率。选取调制信号种类为BPSK、2FSK、2ASK和16QAM,虚警概率设定为0.1,蒙特卡罗仿真次数为5 000次。结果表明:对BPSK与2FSK信号,信噪比为5.7 dB左右时仍能保持检测概率不低于90%;但对2ASK与16QAM信号,同等信噪比下,检测概率分别下降至85%与86%。产生这种差异的原因在于选取作相关的帧时刻是随机的,所以相关统计量max{R(x)}的取值也具有随机性。从统计规律上看,角度调制信号的相关统计量分布相对集中,而幅度调制信号相关统计量分布相对分散,说明相关统计法对不同帧信号幅度差异的敏感性要高于相位差异的敏感性,所以在同等虚警概率下,角度调制信号(BPSK与2FSK)的检测性能要高于幅度调制信号(2ASK)的检测性能。而16QAM信号融合了角度调制与幅度调制,其检测的检测性能介于两者之间,与仿真结论相符。综上,融合帧间相关性的能量检测对角度调制的适应性高于对幅度调制的适应性。 图7 融合帧间相关性的能量检测对不同调制信号的检测概率Fig.7 Detection probability of energy detection fused with interframe correlation on different modulated signals 本文提出一种融合帧间相关性的能量检测方法。该方法在不增加感知用户的前提下,通过增加相关统计量参数,以不同帧间的相关性辅助能量判决,来解决当信噪比较低、噪声存在不确定性时,能量检测性能下降问题。仿真表明,本文方法与直接进行能量检测方法相比,在虚警概率等于0.1,检测概率不低于90%时,所需的信噪比降低了约1 dB。同时,本文方法下单一用户的检测性能,可以接近用户数为2时的双门限协作感知性能。但是,本文方法对幅度调制信号的适应性较差而对角度调制信号的适应性较好。
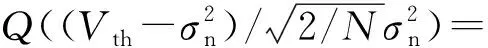
1.3 噪声不确定度

2 融合帧间相关性的能量检测
2.1 相关检测


2.2 融合方案

2.3 步骤流程

3 仿真分析


4 结论

