基于Partial FFT的间歇采样转发干扰抑制方法

李 欣，王春阳，包 磊，付孝龙

(空军工程大学防空反导学院，陕西 西安 710051)

0 引言

间歇采样转发干扰(Interrupted Sampling Repeater Jamming ,ISRJ)以数字射频存储器(DRFM)为基础，通过对线性调频(Linear Frequency Modulation, LFM)信号交替进行存储和转发，能够形成密集的假目标干扰，不仅解决了干扰机干扰大时宽信号时存在的收发隔离问题，也降低了对存储带宽的要求，在针对LFM信号的干扰中得到了广泛的研究和应用[1-2]。

国内外公开文献中针对LFM信号的间歇采样转发干扰进行了大量的研究，先后提出了固定周期间歇采样干扰、参差周期间歇采样干扰、间歇采样循环转发干扰、间歇采样移频转发干扰等，这些干扰样式都是采取“存储-转发-存储-转发”模式工作，区别在于存储的周期和转发时的调制方式不同。文献[3]研究了间歇采样转发干扰的数学原理，并分析了干扰参数对干扰效果的影响。文献[4]以最小错误概率准则下的检测代价为指标，研究了转发频率、占空比和转发功率这三个关键干扰参数对CFAR检测代价的影响。文献[5—10]分别研究了不同干扰参数对间歇采样转发干扰效果的影响以及间歇采样转发干扰在干扰不同体制的雷达中的应用。对于间歇采样转发干扰的对抗技术，文献[11—12]根据间歇采样转发干扰与雷达信号在时频域特征的差异，分别提出了间歇采样转发干扰识别方法，为干扰对抗提供了有效的参考信息。文献[13]根据间歇采样转发干扰信号的时域不连续性，提出了一种基于带通滤波的干扰抑制方法，但是该方法在噪声较大时，难以准确构建带通滤波器。

总体而言，由于间歇采样转发干扰与雷达信号的高度相关性，极大地增加了干扰对抗的难度，因此针对间歇采样转发干扰对抗技术，仍然有待进一步的研究。本文针对间歇采样转发干扰的对抗问题，参考OFDM通信系统Partial FFT解调算法，将Partial FFT算法的分段处理的思想引入雷达干扰对抗中，提出了基于Partial FFT的间歇采样转发干扰对抗方法。

1 干扰信号的作用原理和时频特性

设雷达发射线性调频信号，可表示为：

(1)

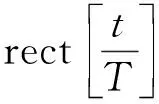
设脉冲压缩参考信号为rref(t)，则回波信号经过脉冲压缩后，可表示为：

(2)

根据间歇采样转发干扰的干扰原理，其干扰过程分为采样阶段和转发阶段，其基本原理如图1所示。间歇采样转发干扰是按照一定周期来进行信号采样和干扰的，在一个干扰周期的起始时间，干扰机首先对一段雷达信号进行采样和存储，之后将前一段时间存储的信号进行多次转发，直到下一周期的采样过程开始。

其信号模型可表示为：

(3)

从间歇采样转发干扰的原理可以发现，该干扰可以看作一个固定周期间歇采样转发干扰的多次延时转发，p(t)的傅里叶级数可表示为：

(4)

式(4)中，fs=1/TS

采样后的干扰信号可表示为：

(5)

从式(5)可以发现，间歇采样干扰信号相当于多个移频干扰信号的加权叠加，移频量为±nfs，与采样脉冲的重复频率有关。

干扰信号经过脉冲压缩后的输出为：

(6)

则间歇采样转发干扰的脉冲压缩输出为：

(7)

根据间歇采样转发干扰的干扰原理，将干扰信号与雷达信号进行对比可发现，在任意子脉冲内，干扰信号与雷达信号的子频带都是不重叠的，干扰和信号的瞬时频率随时间变化规律如图2所示。

从图2可以发现，干扰信号和雷达信号具有不同的时频变化特性，并且两者在任意时刻的瞬时频率都是不同的，这一时频分布特性的差异，为干扰的抑制提供了理论支撑。但是由于间歇采样转发干扰的采样和转发都是在一个雷达脉宽内进行，由此导致信号的线性时频分辨率变差，从而无法利用时频分布的差异实现干扰抑制，而非线性时频变换则存在交叉项，并且通常干扰的功率都强于雷达信号的功率，在时频平面内难以有效提取雷达信号的参数。单纯利用时频分析，难以有效实现对间歇采样转发干扰的对抗，必须针对线性调频信号和间歇采样转发干扰的特点研究新的方法。

2 基于Partial FFT的干扰对抗方法

2.1 信号的分段表示及其频谱

Partial FFT算法是由Yerramalli等人所提出的，一种抑制时变信道OFDM通信系统中的载波间干扰(Inter-Carrier Interference, ICI)的解调算法[14-16]。该算法将一个持续时间为T的信号等分为互不重复的L段，对每段信号补零后做FFT处理，之后对每一个分段的FFT结果乘上一个加权因子后再进行相加，通过选择合适的加权因子即可实现对OFDM通信系统中由多普勒频率所引起的信道时变的有效补偿，从而解调出载波中所携带的信息，并降低ICI。在OFDM通信系统中，由于时变信道的信道参数是未知的，所以通常采用自适应滤波器来估计加权因子。

在OFDM通信系统中，Partial FFT解调的算法处理流程如图3所示[15-16]。

在雷达电子对抗中，雷达接收机接收到回波和干扰的混合信号，可表示为：

s(t)=r(t)+kj(t)

(8)

式(8)中，k表示干信比对应的电压比。

根据Partial FFT的原理，将接收到的混合信号等分为L段，则第l段混合信号可表示为：

(9)

对每一段信号补零后分别做FFT，则第l段雷达信号频谱可表示为：

(10)

根据干扰的原理，可知干扰信号是由采样所得到的雷达信号复制而来，因此每一段干扰信号均与原雷达信号的某一分段相对应，两者之间相差一个固定的延时，该延时量的大小是采样脉宽的整数倍。为了讨论方便，假设Partial FFT的分段数是N(M+1)的整数倍，即不会出现同一分段中包含两个干扰脉冲的分量，则第l段干扰信号的频谱可表示为：

(11)

式(11)中，i=1，2，…，N。

从式(11)可以看出，干扰信号的每一个分段都有与之对应的信号分段，并且第l段雷达信号和第l段干扰信号的中心频率之差为：

Δf=mKτ,m=1,2,…，M

(12)

对于分段后的接收信号，由于干扰信号是通过多次采样转发形成，因此大部分分段是由回波信号和干扰信号叠加而成，对于这些分段，需要根据干扰信号分段与回波信号分段在频率特性上的差异，设计滤波器实现干扰的抑制。

2.2 干扰抑制滤波器的设计

由于第l段雷达信号和第l段干扰信号相差一个固定的频率，因此分段后的信号模型与OFDM系统中，载波间干扰的模型具有相似性，即由于频率的偏移而引入的干扰，区别之处在于OFDM系统中，载波间干扰是由信道时变所引起的，而雷达干扰中，该频偏则是干扰机通过控制转发时间而产生的。在OFDM系统中，通过对每一分段计算加权因子，从而补偿掉时变信道所引起的多普勒频偏，但在雷达抗干扰中，可以对每一段设计特殊的滤波器实现对干扰的抑制，此时，干扰抑制滤波器可类比为Partial FFT中的加权因子。

根据滤波器设计目标的不同可将滤波器分为信号输出最大滤波器、干扰输出最小滤波器和信干比输出最大滤波器，在主瓣干扰条件下，进入接收机的干扰功率较强，为了保证抗干扰的效果，这里以输出信干比作为评价准则来设计滤波器。线性调频信号经过分段后，每段信号的时宽带宽积为：

(13)

根据线性调频信号的性质，当时宽带宽积减小时，其频谱将会展宽，因此在设计干扰抑制滤波器的时候，必须考虑分段后信号频谱的变化和信号的脉冲压缩。

对第l段接收信号，设滤波器的传递函数为Hl(f)，脉冲响应为hl(t)，以第m次转发脉冲为例，则第l段信号的输出信干比可表示为：

(14)

雷达接收信号后续要进行脉冲压缩处理，其中频谱的幅度特性决定脉压后的幅度，而频谱的相位特性决定脉压后输出峰值所在的位置。间歇采样转发干扰主要干扰雷达的测距功能，所以干扰抑制滤波器应当具有不随频率变化的相频曲线，避免引入额外的相位，影响脉压后的距离测量。因此干扰抑制滤波器应当具有不随频率变化的相频曲线，避免引入额外的相位，影响脉冲压缩的结果。根据第l段接收信号的频谱特性，这里以|Rl(f)|作为滤波器的传递函数来实现干扰抑制，由于|Rl(f)|不能直接得到，可以对雷达进行脉冲压缩时的参考信号作同样的分段处理，选取对应的频谱作为传递函数，该频谱具有与|Rl(f)|相同的幅频特性。选取|Rl(f)|作为滤波器传递函数基于以下考虑：1)|Rl(f)|的相频特性恒等于0，并且具有与信号相同的幅频特性曲线，能够最大限度减小对雷达信号的影响；2)由于|Rl(f)|与|Jl(f)|的峰值不在一个频点，可以利用其幅频特性削弱干扰的能量。

(15)

则干扰抑制滤波器的传递函数为：

(16)

根据第l段雷达信号和干扰信号的频谱，可以得出经过滤波后的信号和干扰的频谱为:

(17)

(18)

从式(17)和式(18)可以发现，由于传递函数的幅频特性与雷达信号相同，并且相频特性恒等于0，因此对信号没有影响，而由于干扰信号的峰值与传递函数错开，因此经过滤波器后，干扰的能量被削弱，但是由于分段后频谱的展宽效应，传递函数与干扰信号频谱仍有重叠的地方，因此滤波只能削弱，而不能完全消除干扰。

经过滤波后，削弱了干扰的能量，之后可利用Partial FFT的线性特性，对每一分段分别进行匹配滤波，可以利用匹配滤波函数的幅频和相频特性进一步抑制干扰。根据脉冲压缩的原理，雷达信号的第l段与参考信号的第L-l+1段相互匹配，则对应的参考信号的频谱可表示为：

(19)

式(19)，中t0表示匹配滤波器的固有延时。

因此第l段雷达信号和干扰信号的输出频谱为：

(20)

(21)

第l段接收信号输出的频谱为：

Sl-pc(f)=Rl-pc(f)+kJl-pc(f)

(22)

求和后的时域波形为：

(23)

整个方法的流程为：

1)根据接收信号的时间分布特性进行分段；

2)对分段后的信号补零并做FFT处理；

3)根据参考信号的特性分别计算每一段对应的干扰抑制滤波器；

4)利用干扰抑制滤波器对每一分段信号进行滤波处理；

5)对滤波后的信号分段进行脉冲压缩并求和。

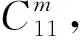
(24)

根据雷达检测的原理和检测代价的定义，大于检测门限的假目标数目越多，则造成的检测代价越高，因此根据干扰抑制前后检测代价的对比可以看出该方法的抗干扰效果。

3 仿真分析

设雷达信号的脉冲宽度为T=100 μs,起始频率f0=0 Hz，调频斜率K=6×1010Hz/s，对应带宽为B=6 MHz，采样脉宽τ=4 μs,采样周期Ts=20 μs不变，转发次数为M=4, 当JSR=20 dB，SNR=0 dB时，脉冲压缩前后的波形如图4所示。

从脉冲压缩的结果可以发现，经过脉冲压缩后，干扰信号能够在真实目标附近形成密集的假目标，并且由于主假目标和次假目标的相互混叠，使假目标的幅度分布表现出近似随机的特性，增加了雷达检测目标的难度。

经过Partial FFT处理后，干扰抑制效果如图5所示。

从图5的仿真结果可以看出，经过滤波和Partial FFT处理，消除了主假目标的干扰，仅保留了部分次假目标，并且剩余的假目标都分布在真实目标附近很小的一个范围内。与采取抗干扰处理之前，图4(b)的脉冲压缩结果相比，对应位置处的假目标幅度下降了5～10 dB，表明该方法可以获得5～10 dB的抗干扰处理增益，有利于目标的检测。

根据线性调频信号的参数，以2/B作为检测单元的宽度，检测单元两侧保护单元数为1，参考单元数为16(即左右各8个)，采用单元平均恒虚警检测，虚警概率为Pfa=10-6，信噪比为SNR=0 dB，则干扰抑制前后的检测门限如图6所示。

假设已知目标位于100 μs处，根据3.2节定义的检测代价，每个SNR和JSR条件下蒙特卡洛仿真1 000次，得到干扰抑制前后的检测代价曲线如图7所示。

根据检测代价的变化曲线可以得出如下结论:

1)经过Partial FFT抗干扰处理后，显著降低了检测代价，表明该方法能够有效减少假目标的数目；

2)进行Partial FFT处理时，增加分段数目可以降低输出信号的检测代价，对抗干扰有利；

3)噪声对抗干扰效果几乎无影响，表现为干扰抑制之后的检测代价基本无影响，这是由于脉冲压缩本身就具有抑制非相关噪声的能力；

4)干信比的增加对抗干扰效果有较为显著的影响，表现为干扰抑制之后，检测代价仍然表现出随干信比增大而增大的现象，这是由于干扰功率的增大，导致干扰抑制后遗留的假目标强度增加。

4 结论

本文提出了基于Partial FFT的间歇采样转发干扰的抑制方法。该方法借鉴OFDM通信系统中抑制载波间干扰的Partial FFT解调算法的思想，在分析间歇采样转发干扰与载波间干扰的信号模型的相似性的基础上，对雷达接收到的回波和干扰的混合信号进行分段滤波处理，实现了对干扰的抑制。

仿真结果表明，该方法对间歇采样转发干扰能够获得5～10 dB的处理增益，应用该方法进行抗干扰处理后，检测代价有了明显的下降，表明该方法对间歇采样转发干扰具有一定的对抗能力。但是，该方法只能部分抑制干扰信号，经过抗干扰处理后，仍然存在剩余的干扰信号，如何进一步提高该方法对间歇采样转发干扰的对抗能力还需要进一步的研究。