基于市场细分的集装箱海运动态定价模型

任斐

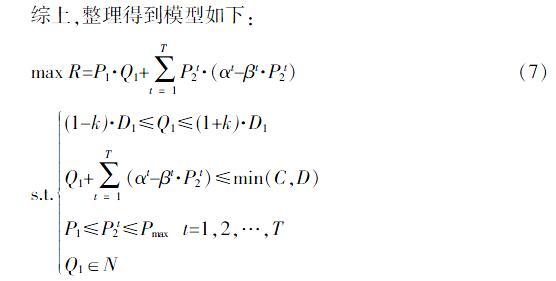
[摘    要] 动态定价在民航和铁路货物运输领域中，已经获得了广泛的的应用研究。文章以海上集装箱运输市场为研究对象，从集装箱海运经营人的角度，基于市场细分和收益管理理论，构建集装箱海运市场动态定价模型，并通过算例对模型进行验证。

[关键词] 动态定价;集装箱运输;收益管理

doi ： 10 . 3969 / j . issn . 1673 - 0194 . 2019. 23. 056

[中图分类号] U169.6;F252.4    [文献标识码]  A      [文章编号]  1673 - 0194（2019）23- 0131- 03

1      引    言

对于集装箱海运经营者来说，运费是其主要营业收入，定价决策的有效性是其企业“生死存亡”的关键。运价和需求之间是反比关系，提高运价将带来需求的减少，反之亦然。如何找到二者之间的平衡点，确定适合的运价，使海运经营者的利益最大化，是集装箱海运企业最关心的问题。

民航客運和铁路货运领域中，已有对动态定价理论动应用的比较熬深入的研究，取得了较好的经济效果。所谓动态定价，就是指企业根据市场需求和自身供应能力，以不同的价格将同一产品在地销售给不同的消费者或不同的细分市场，以实现收益最大化的定价策略。

动态定价的应用有一定的前提条件，比如产品的易逝性，生产能力相对固定，市场供给有上限、客户需求存在差异;需求随时间和价格变化呈现波动性等等。集装箱运输市场恰好也具备这些条件，动态定价方法在集装箱海运市场同样适用。

本文兼顾市场细分和动态定价，从集装箱海运经营人的角度，考虑不同市场的实际营销特点，提出基于市场细分集装箱海运动态定价模型。

2      问题描述

集装箱海运市场上，货主根据其所能提供运输需求在数量和持续性上有很大差别。具有一定规模的生产加工和贸易企业，以及货代企业，在一定时期内具有持续稳定的大量货运需求，是航运企业的“大客户”;针对这部分客户，航运企业通过与之签订运输协议的形式，以优惠的价格换的可靠、充分的货源，从而保证企业的运费收入，这类市场可称之为“协议市场”。

除此之外，市场上还广泛存在零散的少量货运需求，这类“散户”的需求不稳定，数量少，对运价水平和开航时间非常敏感，航运企业需要提供恰当的运价争取货源。

协议市场运价较低且在协议期内相对固定，是航运企业生存运营的基本保障;而自由市场才是航运企业利润的突破口。另外自由市场上，那些临近信用证装运截止日期的需求更注重即时发运，对运价的承受能力较强。基于这一经济现象，可以对自由市场各航次销售期划分为若干时段，采取分时段的动态定价策略。

针对某一航线上，两个港口间的运输业务，以航运企业改航次上的舱位容量为约束，考虑如何分配协议市场与自由市场的舱位方案以及自由市场的不同时段的动态价格，使得航运企业在两个市场上的总收益最大。

3      模型构建

3.1   符号和参数说明

Q1—协议市场实际分配到的舱位（运量），是决策变量;

P1—协议运价，通过销售协议确定;

D1—协议市场的需求;

t—第t个销售时段;

T—自由市场的销售个数;

P2t—自由市场第t销售时段的运价，是决策变量;

Pmax—自由市场运价上限，可以根据历史数据设定;

Q2t—第t时段的分配的舱位（运量）;

根据相关研究成果，海运运价和运量之间存在一定的函数关系，通常讲这种函数关系表述为线性函数，即

Q2t=αt-βt·P2t，t=1，2，…，T（1）

其中，α，β为系数，需要通过历史数据统计分析获得。

R—航运企业的航次总收益，是模型的目标函数;

C—航运企业的舱位容量;

D—航运企业能够获得的总需求预期，可以通过企业历史运量统计获得。

3.2模型构建

航运企业在两个市场获得的总收益R为协议市场运费收益和自由市场各时段收益的综合，即

R=P1·Q1+■P·Q2t（2）

将（1）式代入（2）式，得到本模型的目标函数为：

maxR=P1·Q1+■P2t·（αt-βt·P2t）（3）

假设协议市场的需求相对稳定，每航次的实际运输需求与协议合同中约定的协议运量相当，在一定的范围内上下波动。设波动幅度为k，k取值范围为0到1之间的有理数。则有第一个约束条件，见式（3），表示协议市场获得的舱位要符合运输需求范围。

（1-k）·D1≤Q1≤（1+k）·D1（3）

在航运淡季，或运力供给大于运输需求的情况下，船舶达不到满载;而在旺季，或运力供给小于运输需求的情况下，将出现爆仓。所以，航运企业两个市场上的运量（分配的舱位）之和的上限，应为航线舱容和市场运输总量中的较小值。于是得到第二个约束条件，见式（4）。

Q1+■（αt-βt·P2t）≤min（C，D）（4）

此外，自由市场的运价应高于协议运价，而低于一定的价格水平，因为时间中的市场运价不可能无限提高，基于竞争，运价提升到一定高度后，货主就回转向其他航运企业订舱了。为了简化计算，尽快收敛，在这里，对自由市场的运价设置在一个合理范围内。于是，得到第三个约束条件，见式（5）。

P1≤P2t≤Pmax       t=1，2，…，T（5）

最后一个约束条件，见式（6），表示决策变量Q2t因为正整数。

Q1∈N（6）

综上，整理得到模型如下：

max R=P1·Q1+■P2t·（αt-βt·P2t）（7）

s.t.（1-k）·D1≤Q1≤（1+k）·D1Q1+■（αt-βt·P2t）≤min（C，D）P1≤P2t≤Pmax   t=1，2，…，TQ1∈N

4      模型求解

上述模型并不复杂，其中的相关参数都可以通过历史数据统计获得，利用Lingo、Matlab等軟件自带的工具包就可以进行求解。

5      算例分析

以某航运企业上海到鹿特丹的运营数据为例。每个航次的舱位容量（C）平均为1 533TEU，当前的市场价格上限取值（Pmax）为USD2 400/TEU，根据航运企业以往各航次的总运量，通过统计方法预测出当前市场总需求（D）为1 299TEU。协议需求（D1）为935TEU，平均协议价格（P1）为USD 1 600/TEU，需求变化幅度（k）设为5%。

结合集装箱班轮特点，销售期通常为7天，可以分为三个销售时段，即令T取3。通过这三个销售时段内各自运价和运量数据，可以得到需求和价格函数中的系数α为（406，224，98），β为（0.114，0.057，0.023）。

上述参数代入模型中，对模型求解。得到采用动态定价策略下，协议市场分配得到的舱位Q1为981TEU，自由市场三个销售时段的运价P2=（2 017，2 204，2 427），获得的航次总收益为2 244 633USD。而传统运营和定价模式下的航次总收益为而USD2 230 188，明显低于采用动态定价策略的收益。具体结果如表1所示。

值得注意的是，动态定价策略下为协议市场分配的舱位数已经达到允许的上限，说明客户对运价敏感度较大，运价提高带来的需求下降很显著，要靠更低的运价吸引客户，这与当前航运不景气的现状非常吻合。

由此可见，航运企业基于市场细分，采用分时段的动态定价策略能够有效地提高运营收入。

6      结    语

本文建立的模型打破了传统研究思路，协议市场在舱位分配上的优先权，将自由市场与协议市场的舱位分配和定价策略合并在一个模型中，进行统筹协调，避免机会成本损失。通过算例验证了本文提出的模型的可操作性和有效性。

但本模型只考虑单航次点对点的运输业务，今后的研究可以将研究范围扩大到多点间的集装箱运输业务等。

主要参考文献

[1]计明军，闫妍，祝慧灵. 海铁联运铁路集装箱定价与运营优化[J].中国管理科学，2018（7）.

[2]刘迪，杨华龙，张燕. 多节点集装箱海铁联运动态定价决策[J].系统工程理论与实践，2014，34（1）.

[3]徐光华，丁一，林国龙，等. 沿海捎带集装箱舱位分配与动态定价模型[J].上海海事大学学报，2015（6）.

[4]李冰州. 集装箱班轮二维收益管理在线动态定价策略[J].管理科学学报，2012（8）.

[5]张小强，刘丹，陈兵，等.竞争环境下铁路集装箱班列动态定价与开行决策研究[J].铁道学报，2016，39（2）.