基于凸组合的列文伯格-马夸尔特算法
王贵峰
(亳州职业技术学院,安徽 亳州 236800)
0 引 言
非光滑约束方程组问题在实际经济、工程领域中有着广泛的应用.如在经济学中供应链问题、工程中最优控制及交通平衡等非线性互补问题均可以通过一定的方法转化非光滑约束方程组问题. 非精确列文伯格-马夸尔特算法是一种有效的求解非光滑(连续可微)约束方程组的算法.在局部误差界条件下,文献[1-4]证明了非精确列文伯格-马夸尔特算法超线性收敛.针对非光滑约束方程组的求解问题,文献[5]给出一种精确光滑化列文伯格-马夸尔特算法,该算法具有较好的计算效果.但是,由于该算法在求解约束方程组受初始点和单一形式的步长影响的问题,本文采取凸组合技术(convex combination skill),将L1范数和L2范数并联使用,同时为了进一步改善L-M算法的性能,对已有的步长做出改进,提出一种新的CMLM算法,该算法每步迭代中,可以根据实际情况调整步长,并只需求解一个线性方程组.该算法全局收敛,并在局部误差界条件下,局部二次收敛.实验数据表明,该算法具有良好的计算效果.
1 模型和光滑化函数
考虑非光滑约束方程组
F(x)=0s.t.x∈X,
(1)
其中X={x∈Rn|h(x)≤0},F:X→Rp和h:Rn→Rm均为局部L—连续函数.
题(1)可等价转化成如下无约束方程组
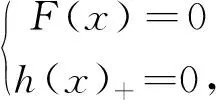
(2)

考虑下列方程组
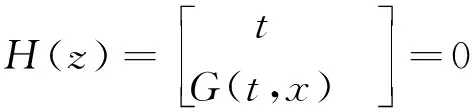
(3)

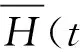
有复合函数性质知,H(·)在R+×Rn上局部L—连续且强半光滑.

z=(t,x)|‖(t,x)-(0,x*)‖≤b2,t≥0
,使得对任意z∈N((0,x*),b2),有c1‖H(z)‖≥dist(z,Z*).
2 一个光滑化的列文伯格-马夸尔特算法

β0=β(z0)∶=γmin
1,‖▽Ψz0‖2
(4)
和

(5)
可知,数列{βk}单调递减,且对任意的z0∈R++×Rn,均有>β0.为了使tk>0恒成立,令.求下列方程的解
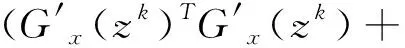
(6)
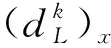
算法

步骤 2 如‖H(zk)‖≤10-6,则终止程序.否则,令αk=min{1,tk/|▽tΨ(zk)|},并由(4)-(5)计算βk.
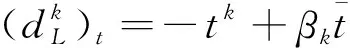
步骤5 如果‖H(zk)‖2>‖H(zk)‖,令δ=0.1+rand*0.1;否则,令δ=0.9+rand*0.1.

对于算法1,有如下定理.
定理1 对任何正整数k≥0,若tk∈R++满足tk≥βk成立,则算法1产生的序列{zk=(tk,xk)},且满足tk∈R++和tk≥βk.
3 收敛性结果
本节将对算法1的收敛性进行分析,设对任意正整数k,均有‖▽Ψ(zk)‖≠0.则算法1 产生无穷序列{zk}.下面给出算法1的收敛性.

现在,我们对算法1的局部收敛性质进行研究.设z*∈Z*是{zk}的一个聚点.有以下定理:

4 数值实验
我们用该算法解带约束非线性互补问题以验证算法1的实用性.非线性互补问题的形式如:求x*∈X={x∈Rn|h(x)≤0},使得x*≥0,P(x*)≥0,(x*)TP(x*)=0,其中P(x)和h(x)函数如以下各问题
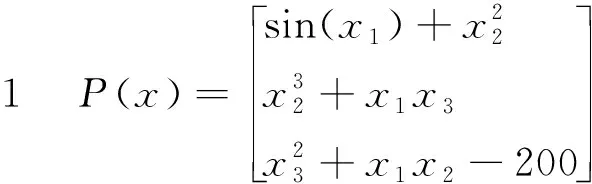

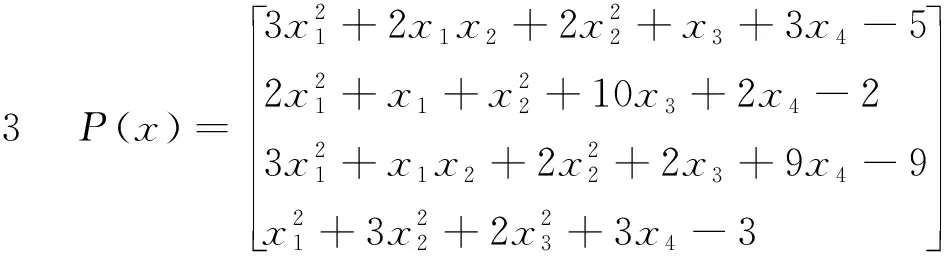
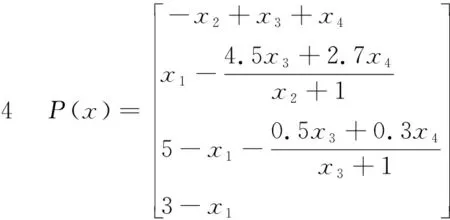

我们采用 Matlab 2010b语言编写该算法的程序,并在惠普台式电脑(pentium(r) dual-core、3.19GHz、2G)上运行程序.所有的数值试验结果见表1和表2.在表1中,“x0”表示迭代初始点,“x*”表示例题的解.表2给出了算法1在求解例题1-4的最后三步迭代中的相关数据,其中“‖H(zk)‖”表示‖H(z)‖在最后三次迭代点处的值,“‖xk-x*‖”表示算法最后三步产生的迭代点与原例题解的距离,表2中的“0”意义为算法所得到的解和原例题真解的距离低于计算机精度,从表2中可看出,该算法确实超线性(局部二次)收敛.

表1:例题1-4的数值试验结果

表2 :问题1-4最后三步迭代的相关数据

