我国财政农业投入对农业产出的影响分析
——基于省际面板数据的分位数回归
袁丽娟 赵 凌 花晨芝
(四川师范大学数学与软件科学学院 四川成都 610066)
我国是农业大国,农业在社会发展中占有重要地位。农业发展状况主要由农业投入产出水平衡量,农业产出水平取决于农业投入的大小,有研究表明[1],财政农业投入和农业产出存在某种长期均衡关系,无论是长期还是短期,财政农业投入是农业产出的原因,并且长期影响远远大于短期影响。为了提高农业生产总值,使得国家对农业的财政支出得到合理分配,需要研究财政农业投入对农业产出的影响。财政农业投入对农业产出的影响有同地区不同时间上投入对产出的影响,也有同时间不同地区的投入对产出的影响等。本文研究不同地区不同时间的投入产出影响,并得到在农业低产出、中低产出、中产出、中高产出以及高产出5个水平上的投入产出影响模型。
对投入产出的影响分析主要包括时间序列分析,截面数据分析以及面板数据分析。齐天真[2]运用DEA法,通过构建基于供给侧的都市农业投入产出指标体系,对天津都市2000-2014年农业的投入产出效率进行了评价,文章的特点是对多投入、多产出的复杂系统进行了评价,局限在于忽略了不同地区间投入产出效率的分析。肖会敏,朱向琳[3]借助多元回归分析方法的相关理论抽了2016年我国农业投入的31个省市的相关截面数据,采用最小二乘法建立模型,找出了我国农业生产总值的主要影响因素,局限是忽略了投入产出在时间上的效应。张亦驰,代瑞熙[4]使用2003-2014年全国30个省的面板数据,对内生性较弱的农业基础设施对农业经济增长的影响进行研究,运用个体和时间双向固定效应模型就前者对后者的影响进行分析,结果表明,农村水利、信息、卫生环境和滞后两期时的交通运输基础设施对农业经济增长有显著的正效应。且选取面板数据进行研究,分析了在时间序列上不同地区投入对产出的影响。
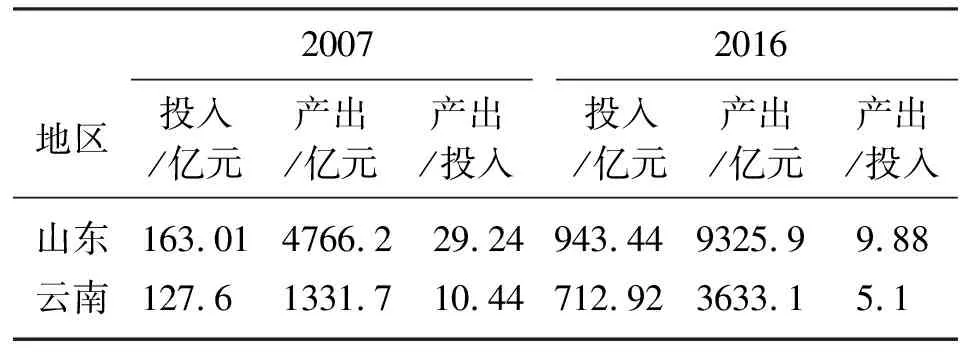
各个地区农业发展状况差别较大,而且随着经济的发展和社会的进步,财政农业投入和农业产出均得到了大幅增长,以山东省和云南省在2007年和2016年的财政农业投入与农业产出数据为例(表1):
比较表中数据可以发现在这两年里,当财政农业投入相等时,山东省的农业产出值更大;两个省在2016年的财政农业投入与农业产出,均比2007年上涨了许多。因此采用面板数据模型,考虑时间序列上不同地区财政农业投入对农业产出的影响更具有现实指导价值。
表1 财政农业投入与农业产出
20072016地区投入/亿元产出/亿元产出/投入投入/亿元产出/亿元产出/投入山东163.014766.229.24943.449325.99.88云南127.61331.710.44712.923633.15.1
建立面板数据模型进行投入产出影响分析时,最早出现的参数估计方法为最小二乘法。如陈丽竹,周文兴[5]利用1993-2014年我国31个省的面板数据,利用最小二乘法找出了农业全要素生产率增长的影响因素。运用最小二乘法建立的面板数据模型中的系数,反映出在财政农业投入的变化对农业产出均值的影响,而无法关注到在不同的产出水平的条件分布特征上投入对产出的影响大小。本文采用分位数回归方法建立面板数据模型,研究财政农业投入对农业产出的影响。分位数回归可以得到在不同产出水平的条件分布特征上的影响系数,即不同分位点上投入对产出的影响。
面板数据的分位数回归方法的理论研究日益完善,在近些年来得到了广泛的应用,张晶,王淼晗,方匡南[6]利用2002—2009年我国30个省市自治区的省际面板数据,运用面板数据固定效应变换分位数回归方法对影响我国城乡居民收入的影响因素进行了实证分析;李群峰[7]对分位数回归基本原理在面板数据模型中的应用作了深刻分析,利用1998—2006年25个行业企业销售收入与专利申请数量的面板数据,分别采取最小二乘法和分位数回归法进行参数估计,并对结果进行比较分析,发现用分位数回归方法在面板数据模型估计时具有明显优势。
本文对2007-2016年我国31个省市自治区省际面板数据建立了面板数据分位数回归模型,从全国、东部、中部以及西部地区的区域角度出发,分析在不同分位点上财政农业投入对农业产出影响效应的差异,并将面板数据最小二乘法和面板数据分位数回归方法的结果进行了对比分析,研究如何通过调节我国财政农业投入在不同分位点以及不同区域的分配提升农业产出水平。
一、面板数据分位数回归的基本原理
(一)分位数回归的基本原理
相较最小二乘估计,分位数回归具有以下优势:(1)分位数回归不对模型中的随机误差项做正态分布的假设,能够减少对残差分布的限制,在扰动项非正态的情况下,分位数估计量相较于最小二乘估计量更加有效,不需要满足最小二乘法要求的Gauss-Markov条件,适合具有异方差的模型。(2)最小二乘法估计的模型反应的是条件意义下的均值,反应的是自变量变化对因变量的平均值的影响,而分位数回归能估计出回归估计量在不同分位数水平下的不同参数值,更加细致地描述因变量和自变量之间的关系。(3)最小二乘法是通过最小化残差平方和进行参数估计,分位数回归是通过使得加权残差绝对值之和最小求出参数的估计值,因此对异常值的敏感程度较小,参数估计更加稳健。(4)分位数回归还具有单调同变性,可对回归过程中不平稳的样本数据进行转化处理,而不影响估计效果。
分位数回归的基本思想和系数估计:
假设随机变量的分布函数为
F(y)=P(Y≤y)
(1)
的分位数定义为满足的最小值,即
q(τ)=inf{y∶F(y)≥τ},0<τ<1
(2)
可由如下的经验分布函数代替:
(3)
式中,yi(i=1,2,…N)为样本观测值。
根据分位数回归的思想,FN(y)的τ分位数q(τ)可以由最小化关于ζ的目标函数得到,即
(4)
式中argminζ{·},函数表示取函数最小值时ζ的取值,ρτ(u)=u(τ-I(u<0))称为检查函数,依据u取值符号进行非对称的加权;I(u)是指示函数,u是条件关系式,当u为真时,I(u)=1;当z为假时,I(u)=0。式(4)中的条件关系式u为yi≤y,当yi≤y时,I(yi≤y)=1,否则取值为0。通过对此最小化问题进行考察便可知FN(y)的τ分位点值是上述优化问题的解。
现假设因变量Y的条件分位数由k个解释变量组成的矩阵X线性表示:
q(τ|xi,β(τ))=xiβ(τ)
(5)
式中,xi=(x1i,x2i,…,xki)为解释变量向量,β(τ)=(β1,β2,…,βk)′是τ分位数下的系数向量。当τ在(0,1)上变动时,通过求解下式就可以得到分位数回归的参数估计:
(6)
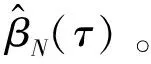
(二)面板数据模型思想
面板数据具有截面和时间两个维度的二维数据,从横截面看,面板数据是在某一时间节点上,由若干个个体组成的截面观测值,从纵截面看,是每一个个体在相同时间段内的时间序列数据。
目前我们所熟知的面板数据分析方法只能用在平稳的面板数据上,为了防止面板数据各序列之间的伪回归,需要先对数据序列进行平稳性检验——单位根检验。学者们刚开始时提出的单位根检验只适用于时间序列数据,而面板数据是包括时间和截面的二维数据,从截面来看,是某个个体的时间序列数据;从时间层面来看,则是某一个时间点上若干个体的样本观测值。随着对面板数据和时间序列单位根检验法的研究,有了面板数据的单位根检验[7]。
1. 面板数据平稳性的定义与检验
现有的面板数据的分析方法只适用于平稳的面板数据,因此在进行面板数据相关研究时,第一步就是判断面板数据是否平稳。
平稳过程的定义:对于随机面板数据{Xit}(i=1,2,…;t=1,2,…)若Xit满足下列条件
(1)对任意的i,t,都有均值E(Xit)=μ;
(2) 对任意的i,t,都有方差Var(Xit)=σ2;
(3) 对任意的i,t,都有协方差Cov(XitXi+ht+k)=γhk。则称面板数据序列平稳。
通过对数据序列的单位根检验判断序列的平稳性,若检验的结果为随机序列拒绝存在单位根的假设,表明数据序列是平稳的,可直接用于建模,否则表明数据序列非平稳。
对于非平稳的序列,通过差分运算或者其他变换,观察能否得到具有平稳性的序列,即判断是否为单整序列。当解释变量和因变量都是同阶单整序列时,可进行协整检验。协整检验是确定变量之间是否存在长期稳定的均衡关系的方法。所谓的协整是指若两个或多个非平稳的变量序列,其某个线性组合后的序列平稳,称这些变量序列间有协整关系存在。若变换后得到的平稳的序列间存在协整关系,便可使用变换后的序列建立模型。
面板数据单位根的检验方法分为两类,一类为相同根情形下的单位根检验包括LLC检验、Breitung检验和Hadri检验,原假设为存在普通的单位根过程;另一类为不同根情形下的单位根检验包括Im-Pesaran -Shin检验、Fisher-ADF检验和Fisher-PP检验,原假设为存在有效的单位根过程。
2.面板数据分位数回归模型及参数估计
将分位数回归方法应用于面板数据模型中,就是运用分位数回归方法对面板数据模型进行参数估计,得到的面板数据分位数回归模型与截面数据上的分位数回归模型具有类似的形式。考虑如下面板数据模型:
Yit=αi+Xitβ+μit,i=1,2…,N,t
=1,2,…T
(7)
Xit=(X1it,X2it,…,XKit),β
=(β1,β2,…,βk)′
(8)
该模型表示面板数据中包括N个截面成员和T个时间点。其中μit为误差项,K为解释变量个数,αi为截距,截距项分为三种类型,一是无个体影响的截距项,即α1=α2=…=αN,称为混合效应;二是个体影响与解释变量相关的截距项,称为固定效应;三是个体影响与解释变量不相关的截距项,称为随机效应。
在计量经济学中,用于检验固定效应还是随机效应的方法为Hausman检验法,其原假设为个体影响与解释变量不相关,应建立随机效应模型,若检验结果拒绝原假设,选择固定效应;用于检验模型具有混合效应还是固定效应的方法为似然比检验法,其原假设为相等,应建立混合效应模型,若检验结果拒绝原假设,选择固定效应。
Koenker[8]指出面板数据分位数回归模型在形式上与截面数据下的分位数回归非常类似,由分位数回归的参数估计可推导出面板数据分位数回归模型的参数估计式为:
(9)
其中条件分位数函数为
qyit(τ|xit)=xitβ(τ)+αi(τ)
(10)
二、实证分析
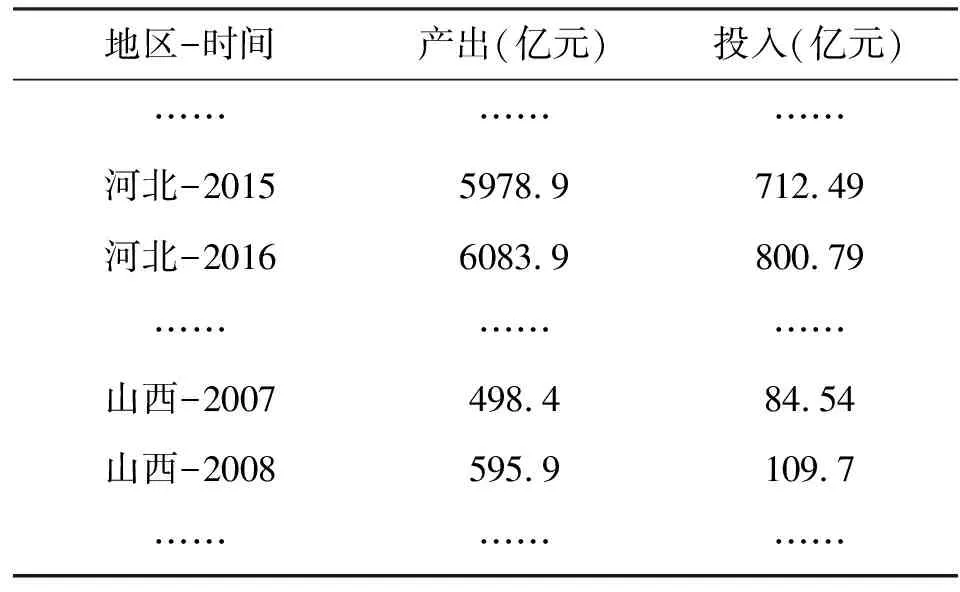
本文对中国2007-2016年10年来31个省市自治区的面板数据进行分析,财政农业投入(以下用AFE表示)与农业产出(以下用AOV表示)的数据分别来源于《中国统计年鉴》,以财政农业投入表示国家农、林、牧和渔业财政支出,农业产出表示农、林、牧和渔业总产值(单位均为:亿元),表2为取到的部分原始面板数据,如下。
表2 农业产出与农业投入的面板数据(部分)
地区-时间产出(亿元)投入(亿元)………………河北-20155978.9712.49河北-20166083.9800.79………………山西-2007498.484.54山西-2008595.9109.7………………
为了消除异方差的影响,本文将所有变量都做取自然对数的处理。
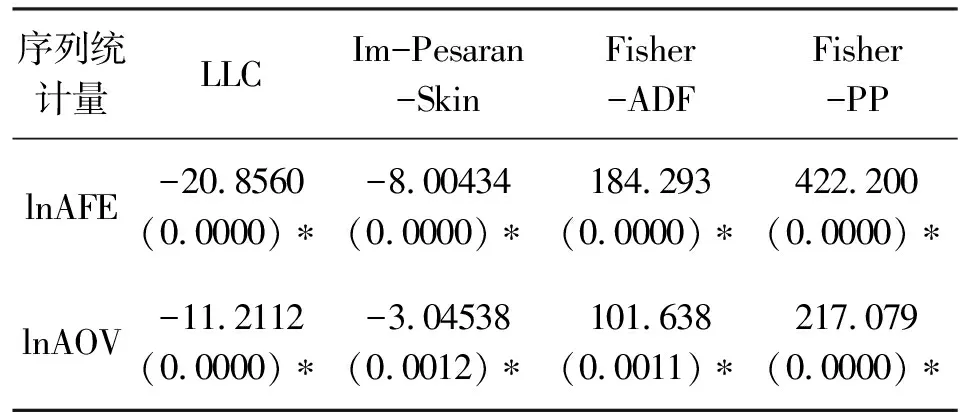
检验面板数据平稳性的标准方法是单位根检验,运用Eviews对数据进行单位根检验的结果如下:
表3 两变量序列的单位根检验结果
序列统计量LLCIm-Pesaran-SkinFisher-ADFFisher-PPlnAFE-20.8560(0.0000)∗-8.00434(0.0000)∗184.293(0.0000)∗422.200(0.0000)∗lnAOV-11.2112(0.0000)∗-3.04538(0.0012)∗101.638 (0.0011)∗217.079(0.0000)∗
注:()内为P值;加“*”表示在5%的显著性水平下拒绝原假设而接受备择假设;根据面板数据时序图,序列lnAFE、lnAOV均选择含截距项,不含时间趋势项。
从检验结果表可以看出,序列lnAFE与lnAOV在LLC检验、Im-Pesaran-Skin检验、Fisher-ADF检验和Fisher-PP检验下均拒绝单位根的存在,两个变量序列均平稳。
确定截距项的影响效应,进行了Hausman检验和似然比检验,结果如下:
表4 Hausman检验和似然比检验结果
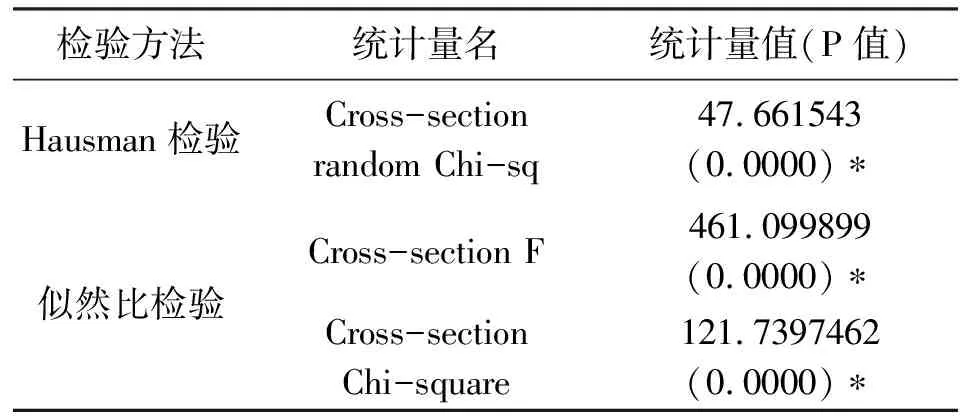
检验方法统计量名统计量值(P值)Hausman检验Cross-sectionrandom Chi-sq47.661543(0.0000)∗似然比检验Cross-section F461.099899(0.0000)∗Cross-sectionChi-square121.7397462(0.0000)∗
注:加“*”表示在5%的显著性水平下拒绝原假设。
Hausman检验的原假设是建立随机效应模型,似然比检验的原假设为建立混合效应模型。观察表中结果可知,两个检验的结果都是要建立个体固定效应模型。结合模型前面要建立变截距模型的结果,本文中的数据应建立个体固定效应模型。
面板数据模型采用的最小二乘法,能够反映财政农业投入对农业产出均值的影响,而为了分析在不同农业产出水平上财政农业投入对农业产出贡献率的变化规律,以及其在不同区域间的差异情况,本文对各个区域采用了面板数据分位数回归方法进行分析,将各个区域的农业产出值进行排序后,选择0.1、0.25、0.5、0.75和0.95分位点分别代表农业低产出、中低产出、中等产出、中高产出以及高产出的地区,用面板数据分位数回归方法进行参数估计。各分位点估计的回归系数反映的是不同分位水平下农业投入对农业产出影响的大小。本文采用R统计软件,在quantreg软件包下,采用自举法(Bootstrap)[11]进行分位数回归的计算。分别以全国的31个截面,东部地区的11个截面,中部地区的8个截面以及西部地区的12个截面进行面板数据分位数回归估计和最小二乘估计。估计结果见下表:
表5 农业投入的弹性系数
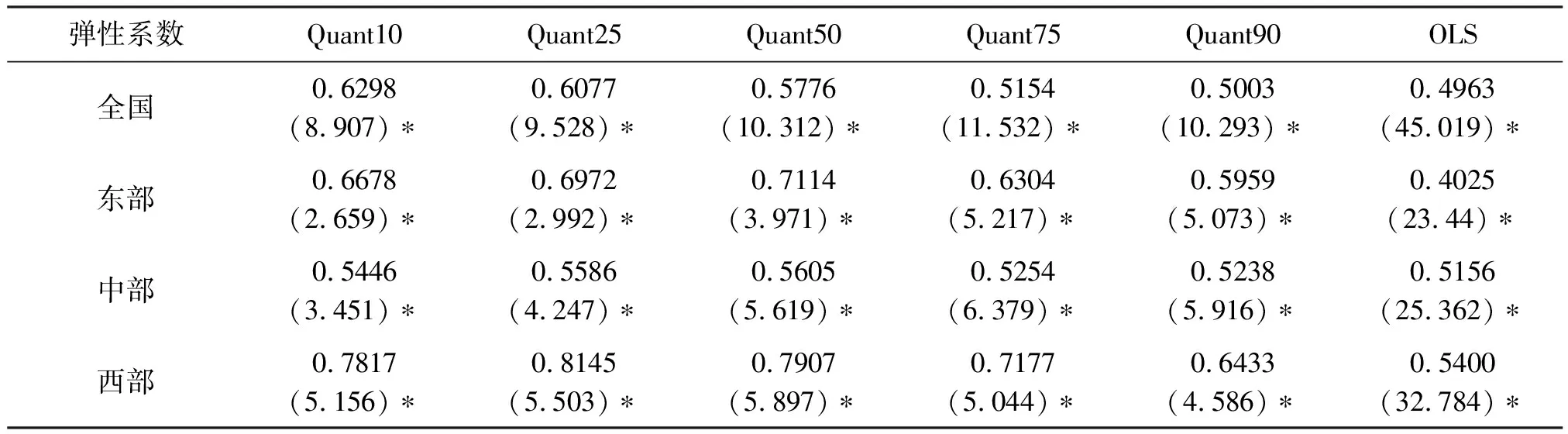
弹性系数Quant10Quant25Quant50Quant75Quant90OLS全国0.6298(8.907)∗0.6077(9.528)∗0.5776(10.312)∗0.5154(11.532)∗0.5003(10.293)∗0.4963(45.019)∗东部0.6678(2.659)∗0.6972(2.992)∗0.7114(3.971)∗0.6304(5.217)∗0.5959(5.073)∗0.4025(23.44)∗中部0.5446(3.451)∗0.5586(4.247)∗0.5605(5.619)∗0.5254(6.379)∗0.5238(5.916)∗0.5156(25.362)∗西部0.7817(5.156)∗0.8145(5.503)∗0.7907(5.897)∗0.7177(5.044)∗0.6433(4.586)∗0.5400(32.784)∗
注:括号内为t统计量;*表示在5%的显著性水平下拒绝原假设。
从上述结果表可以看出,最小二乘回归和分位数回归的系数均显著变化,系数的最小值为0.4025,表明财政农业投入对农业产出具有显著的正向影响。基于各变量的数据都做了取自然对数的处理,结果表中的系数表示的是财政农业投入的变化引起农业产出的变化的速率,系数越大,变化速率越快,财政农业投入的增加能更快地引起农业产出的增加。
比较表5最后一列采用最小二乘法得到的面板数据模型系数,可以发现东部地区的财政农业投入对农业产出的影响最小,这是由于中、西部地区中多数省份农业产值和农业人口占比仍然较大,农业生产条件相对较差,许多农业基础设施的供给不足,增加财政农业投入额能够较快速地完善农业基础设施,改善农业生产条件,使得财政农业投入对农业产出的作用相比东部地区而言更加明显,因此东部地区农业产出在均值意义下对财政农业投入的依赖程度最小;西部地区的财政投入对农业产出的影响最大,主要由于我国西部地区农业土地面积为541.4万平方公里,占全部国土面积的56.4%,耕地面积多,乡村人口数比重大,农业发展在经济发展中占有主要地位,使得农业产出更多地依赖于财政农业投入;中部地区财政农业投入对农业产出的影响居于东部地区与西部地区之间。
如图1,比较分位数回归得到不同产出水平下财政农业投入对农业产出的影响系数,可以发现全国31个截面地区随着分位数的增加,回归系数逐渐减小,这表明在农业产出较低的地区,农业发展相对落后,财政农业投入更大程度地决定了农业产出,农业产出高的地区,农业产出的水平更多地取决于其他的影响因素。
从这5个分位点的结果来看,东、中、西部地区随着分位数的增加,回归系数是先增后减的趋势,西部地区在0.25分位点处最大,也就是在西部的12个省市自治区中,农业中低产出水平的地区的财政农业投入对农业产出的影响最大;东部11个截面地区和中部8个截面地区在0.5分位点处系数最大,即两个区域各自农业中等产出水平地区的财政农业投入对农业产出的影响最大。因此,在各个区域中进行财政农业投入分配时,应该优先考虑增加对西部的中低产出水平,东部和西部的中等产出水平的省市自治区的投入。
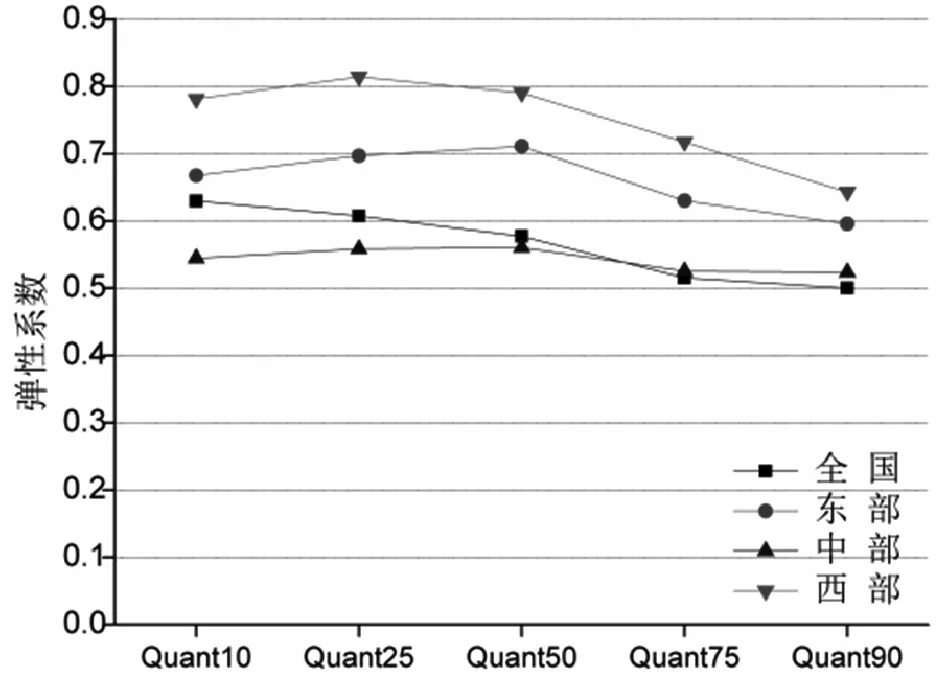
图1 各区域弹性系数随分位点变化的趋势
分位数回归的结果不仅可以从全国31个省市自治区的不同农业产出水平上反映财政农业投入对农业产出的影响,还可以更加全面地刻画不同区域的农业产出水平上财政农业投入对农业产出的影响。这也为财政农业投入的分配提供了两种方法,第一种是先根据东、中、西三个区域最小二乘回归的结果进行分配,其中西部地区系数最大,则优先增加西部地区的财政农业投入,其次为中部地区,最后是东部地区;再根据各自区域不同农业产出分位点对应的省市自治区的回归系数大小进行选择,系数越大,农业产出增加得越快。第二种是直接根据全国31个省市自治区面板数据分位数回归的结果,分位点越低,回归系数越高,在进行财政农业投入分配的时候,侧重加大对农业低产出,中低产出地区的扶持,在增加各个地区的财政农业投入时,这些地区能比农业产出水平更高的地区更快速地引起农业产出的提高。
三、结论与政策建议
通过对31个省区市2007-2016年的面板数据分析,10年中,各个地区的财政农业投入和农业产出均得到了大幅提高,充分体现了国家和政府对农业发展的重视,以及我国农业发展的进步。同时,各个地区财政农业投入和农业产出的增长水平有所不同,财政农业投入的增加所引起的农业产出的增长速率也存在差异。因此,本文利用面板分位数回归方法估计了各区域财政农业投入在各分位点上对农业产出的影响大小,揭示了在各区域财政农业投入对农业产出在不同分位点水平下的变化规律及差异。基于实证分析的结果可知,不管基于全国还是东、中、西部地区的估计都表明财政农业投入对农业产出具有显著的正向作用,因此应当加大财政农业投入力度;从全国的面板数据分位数回归模型的结果看,农业产出水平越低,财政农业投入对农业产出的影响越大,因此要优先增加对农业低产出地区的投入;不同区域中农业产出水平的条件分布特征有所不同,从区域角度进行分配时,要着重加大对大西部地区的财政农业投入,从各个区域分配到各个省市自治区时,要根据不同区域的分位数回归结果,进行合理分配;在各分位点水平上,财政农业投入对农业产出的影响在西部地区最大,在均值意义下也是如此,一方面,我国西部地区经济不发达,影响农业产出的水平更多地取决于国家对农业的财政支出,另一方面,耕地面积大使得农业发展在经济发展中占有很大比重,基于此,应当大力发展西部地区的农业经济,发挥其区域优势,在财政农业投入的分配过程中侧重增加对西部地区的财政农业投入。

