工科专业量子力学课堂教学探讨

钟志有，龙 浩

(中南民族大学 电子信息工程学院，湖北 武汉 430074)

1 引言

量子力学是研究微观粒子运动规律的理论，它不仅是现代物理学的两大基本支柱之一，而且在化学、生物学、材料学和宇宙学等有关学科和许多近代技术中得到了广泛的应用[1～5]。量子力学是高等院校中光电专业的一门基础课程，同时也是许多理工科专业的学科基础必修课程之一。作为一门建立在公理体系上的科学，量子力学对初学者来说普遍感到物理概念生涩难懂、数学工具高深、课本难读、习题难做，学习和掌握的难度很大[6～10]，因此，如何结合学生的实际，采取合适的教学方法使学生理解其物理思想，已经成为量子力学课堂教学中的一个重要课题。本文分别以一维线性谐振子和一维无限深方势阱作为实例，阐述了类比方法和模拟分析在量子力学教学中的应用，调动了学生的学习积极性，提高了课堂教学的效果。

2 类比方法的运用

类比方法是根据两个不同对象的部分属性相似而推出这两个对象其他属性也可能相似的一种逻辑推理方法，它是一种从特殊到特殊的推理方法，是人类认识自然的重要方法[11～15]。类比方法不仅可以用于抽象概念的讲授中，面且也可以用于Schrödinger方程的求解。对于某些势函数，其Schrödinger方程可以通过一定的数学变换，化为能严格求解的Schrödinger方程形式，将其解与已知的精确解进行类比，按照精确解的形式直接写出相应的解[1,3]，特别是，这种方法很容易将相应的能级表示出来。

如果一维线性谐振子受到附加势场的扰动[1]，其Hamilton算符可表示为：

(1)

对应的定态Schrödinger方程为：

(2)

为了求解方程(2)，可以首先考虑没有受到扰动的一维线性谐振子问题，这时其Hamilton算符为：

(3)

相应的定态Schrödinger方程为：

(4)

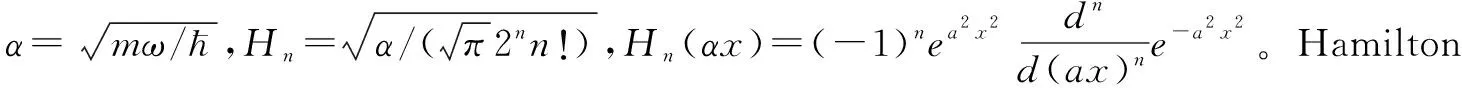
(5)

式(5)中，x′=x-λ/(mω2)。由(5)看出，该问题仍然属于一维线性谐振子，它的每一个能级都比未受扰动时线性谐振子的能级降低了λ2/(mω2)，同时其平衡点向右移动了λ/(mω2)[1]。通过类比方法容易得出，受到-λx扰动后的定态波函数和能级可以分别表示为：

ψ(x′)=Nne-α2x′2/2Hn(αx′)

(6)

(7)

由此可见，利用类比方法很容易得到受扰动后一维线性谐振子的定态波函数和能级表达式。

MATLAB模拟分析

MATLAB软件不仅具有强大的数值计算能力和功能齐备的可视化能力，而且还具有简单易学、运算效率高、应用范围广等特点[16～18]，是目前最为流行的一款数学工具软件，它已经广泛应用于各行各业的许多领域中[19～28]。本文中将MATLAB软件应用于量子力学教学过程，大大激发了学生的学习兴趣，提高了课堂教学的效率，起到了事半功倍的作用。

对于一维无限深方势阱中的粒子[3]，其势能如下：

(8)

在势阱外，由于无限大，粒子不能运动到势阱之外，所以其定态波函数。在势阱内，，此时粒子的波函数满足定态Schrödinger方程：

(9)

根据波函数的连续性，可以得到粒子的分立能级和归一化波函数分别如下：

(10)

(11)

对于一维无限深方势阱中的电子，其质量为m=9.1×10-31kg，设势阱宽度a=4 nm，利用MATLAB语言编写程序，可以得到其波函数和概率密度曲线如图1所示。由图可见，粒子在势阱中出现的概率因地而异，在阱壁处的概率为零；另外概率密度分布还随量子数n而变化，模拟结果与理论分析完全相符[1,3]。

图1量子数n为1、2和3时粒子的波函数和概率密度的曲线

4 结语

量子力学是中南民族大学光电专业的专业必修课程之一，针对学生量子力学学习中存在的困难，我们采用形式多样的教学方法，激发了学生的学习兴趣，提升了课堂教学水平，学习效果得到了明显提高。然而这门课程的教学仍然存在教学手段单一、与生产实践结合不紧密等问题，这些都有待于在今后教学中加以改进。