瓦斯爆炸隧道内冲击波特征及衬砌损伤机制数值研究

李志鹏， 韩龙强， 崔柔杰， 陈 文

(1. 北京科技大学土木与资源工程学院， 北京 100083;2. 玉溪市晋红高速公路投资发展有限公司， 云南 玉溪 653100)

0 引言

隧道工程对完善交通网络有着重要作用。无论在建设阶段还是运营阶段，隧道的安全性始终为第一要素，而隧道内发生爆炸事故无疑是严重的隧道安全事故。例如，当隧道穿越富含瓦斯地层时，施工中稍有不慎便会引发瓦斯爆炸，不仅会造成重大人员伤亡与经济损失，还会使隧道结构受损，给隧道爆炸致灾后的重建修复工作造成巨大困难。瓦斯爆炸属于气体爆炸，气体爆炸在事故伤害阶段的破坏形式为冲击波超压、热辐射以及抛射碎片，其中重点是超压冲击波，不仅造成人员伤亡，更导致隧道衬砌结构严重受损。因此，研究隧道内爆炸冲击波的强度及冲击波流场特征对隧道或大型地下结构的影响具有重要意义。

关于隧道内爆炸的问题，杨科之等[1]通过总结试验结果并拟合计算结果得到直边墙拱形隧道内爆炸冲击波的传播规律； 庞伟宾等[2]通过试验研究得到爆点在不同位置爆炸作用下适用于直边墙拱形隧道内爆炸冲击波到时、速度预测公式； 吴世永等[3]基于自由场爆炸冲击波压强预测公式，通过对直边墙拱形隧道内冲击波衰减规律修正，得到隧道内爆炸冲击波压强预测公式； 田志敏等[4]通过有限元计算，分析了炸药形状、爆点位置对圆形隧道内爆炸荷载分布的影响，并给出了衬砌结构上反射超压峰值的经验公式。随着计算机技术及计算动力学的快速发展，已有学者通过大型显式动力学软件研究隧道内的爆炸问题。陈常宇等[5]、张小勇等[6]采用AUTODYN软件研究了隧道内爆炸作用下衬砌结构的动力响应及损伤机制； 孔德森等[7]采用显式动力学软件LS-DYNA研究了地铁隧道在10 kgTNT爆炸作用下的冲击反应。以上学者的研究成果对隧道内爆炸的研究方法、材料模型选择均具有积极的指导作用，但是否适用于实际工程未曾可知。且当前对公路隧道内剧烈爆炸问题鲜有研究。

本文使用显式动力学软件LS-DYNA对洛带古镇隧道内瓦斯爆炸问题进行数值研究。在总结前人研究成果的基础上，基于等效爆能理论对瓦斯爆炸量化研究，建立与隧道几何结构一致的流固耦合数值模型，采用RHT模拟衬砌并对关键参数进行修正，对隧道内爆炸冲击波流场进行研究并与经验解析式对比，同时分析了衬砌的损伤机制，并将研究结果与现场衬砌损伤调查情况进行对比。

1 工程背景

洛带古镇隧道位于四川省成都市天府新区，是成洛大道东延线的控制性工程。隧道全长2 920 m，自西向东横穿龙泉山脉，隧道地处川中天然气田分布区，前期勘察阶段测得隧道进口段瓦斯最大溢出量为0.52 m3/min，判定为高瓦斯隧道[8]。2015年2月24日，洛带古镇隧道进口段发生瓦斯爆炸，如图1(a)所示，爆炸威力巨大，隧道结构损伤严重。事故调查结果显示，左洞有1个爆点(ZK2+810)，如图1(b)所示； 右洞有2个爆点(ZK2+300、ZK2+587)，如图1(c)所示。本文选取洛带古镇隧道左洞爆炸受损部分区域(ZK2+790～ZK2+830)进行研究，该区段二次衬砌结构为厚40 cm的C25素混凝土结构。

(a) 隧道爆炸现场图

(b) 隧道左洞爆点示意图

(c) 隧道右洞爆点示意图图1 洛带古镇隧道爆点位置及爆炸现场情况Fig. 1 Explosion positions and field explosion situation of Luodaiguzhen Tunnel

2 爆炸荷载

瓦斯爆炸事故为突发不可预知事件，其本质是可燃气体的快速燃烧。在隧道这类长径比较大、内部结构复杂、施工设备(障碍物)较多的密闭结构内，瓦斯爆炸通常由爆燃转为爆轰状态[9]，而且爆炸前隧道内瓦斯体积分数、积聚区位等均难以准确计算，因此需寻求一种等效方法量化隧道内瓦斯爆炸。当前，多数学者采用TNT当量法[10-14]研究巷道内瓦斯爆炸问题[12]和易燃易爆物的爆炸问题[13]，而对隧道内瓦斯爆炸问题采用TNT当量法进行研究的案例鲜有。此外，在LS-DYNA中，TNT材料常用于模拟爆轰现象。

瓦斯是多种气体的混合物，主要可燃物为甲烷(CH4)，密度为0.716 kg/m3，当瓦斯中甲烷含量达9.5%时瓦斯爆炸威力最大[9]。本文考虑最不利情况，即甲烷完全燃烧，爆炸威力最大。由式(1)可知甲烷完全燃烧时放热量为55.64 MJ/kg。

CH4+2O2→CO2+2H2O+890.3 kJ

。

(1)

TNT当量法采用等效爆能原理，将瓦斯爆炸产生的能量(爆热)转化为一定当量的TNT，如式(2)—(3)所示。

Eq=QG/QTNT

；

(2)

MTNT=α·Eq·VG·ρG。

(3)

式(2)—(3)中：Eq为瓦斯的TNT当量比；QG为甲烷爆热，MJ/kg；QTNT为TNT爆热，一般取为4.5 MJ/kg；α为瓦斯中甲烷含量百分比；VG为甲烷体积，m3；ρG为甲烷密度，kg/m3。

此次爆炸事故发生在春节假期期间，其间隧道10 d未通风。本文研究区段在施工期间检测到实际瓦斯溢出量为1.08 m3/min，计算可知隧道内已充满瓦斯气体，隧道断面面积为72.34 m2，故隧道内积聚瓦斯总体积为2 893.6 m3。由式(2)—(3)可得隧道内积聚瓦斯的量化值MTNT为2 428.9 kgTNT。

3 数值模型及材料参数

3.1 数值模型

LS-DYNA中的ALE(arbitrary lagrangian eulerian)建模技术可以实现爆炸冲击波与隧道衬砌的相互作用。根据研究区域内隧道标准横断面设计图(见图2)，构建“爆源-空气-衬砌-围岩”的流固耦合数值模型。模型横断面如图3(a)所示，爆心位于隧道中心，距拱顶和底板均为3.6 m。数值模型尺寸为40.00 m×17.64 m×15.70 m(长×宽×高)，边界条件设置为无反射边界以模拟无限域，如图3(b)所示。

图2 隧道横断面设计图 (单位： cm)Fig. 2 Design sketch of tunnel cross-section (unit: cm)

(a) 数值模型横断面

(b) 模型边界条件图3 数值模型及边界条件 (单位： m)Fig. 3 Numerical model and boundary conditions (unit: m)

3.2 空气参数

空气的模型及状态方程分别采用LS-DYNA中*MAT_NULL模型和*EOS_LINEAR_POLYNOMIAL[15]，计算参数如表1所示。

表1 空气计算参数Table 1 Calculation parameters of air

3.3 TNT参数

TNT的本构模型及状态方程分别采用LS-DYNA中*MAT_HIGH_EXPLOSIVE_BURN、*EOS_JWL[15]，计算参数如表2所示。

表2 TNT计算参数Table 2 Calculation parameters of TNT

3.4 衬砌参数

RHT模型能更好地模拟爆炸冲击荷载作用下混凝土的力学特性[16-17]。RHT模型由W. Riddel提出,并有一套标准参数[18]。RHT模型通过引入图4(a)中所示的弹性极限面、最大失效面和残余强度面分别表示混凝土的弹性极限强度、最大失效强度和受损残余强度，有效呈现了混凝土材料在爆炸冲击荷载作用下的弹性变形阶段、线性强化阶段和损伤软化阶段，如图4(b)所示。

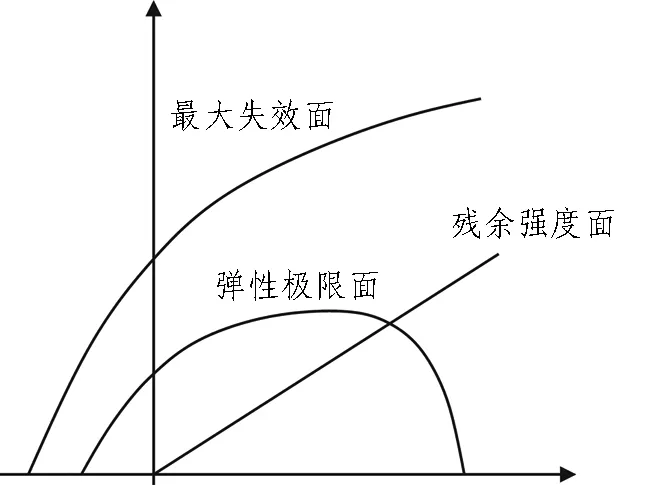
(a) RHT模型3个极限面

(b) 混凝土“三阶段”示意图图4 RHT模型示意图Fig. 4 Sketches of RHT model

RHT模型中的最大失效面方程、弹性极限面方程以及残余强度面方程如下：

(4)

Felastic·Fcap；

(5)

σresidual=Af×(p*)Nf

。

(6)

洛带古镇隧道衬砌结构为C25混凝土，在数值计算中衬砌结构的单轴抗压强度取25 MPa，压缩应变率指数βc和拉伸应变率指数βt由式(7)、(8)计算而得[18]，分别为0.042和0.044。

βc=4/(20+3fc)

;

(7)

βt=2/(20+fc)

。

(8)

RHT模型累积损伤定义为：

(9)

(10)

综上，RHT模型中部分关键参数修正后如表3所示，其余参数与原参数表中一致。

表3 RHT模型的计算参数Table 3 Calculation parameters of RHT model

3.5 围岩参数

洛带古镇隧道围岩主要为砂岩及中—厚层状弱风化泥岩夹砂岩，围岩级别为Ⅳ—Ⅴ级。在爆炸作用下，围岩应变率效应显著，LS-DYNA中*MAT_PLASTIC_KINEMATIC适用于描述材料显著的应变率效应，该模型经证明适用于模拟爆炸荷载下围岩特性[20]。围岩计算参数如表4所示。

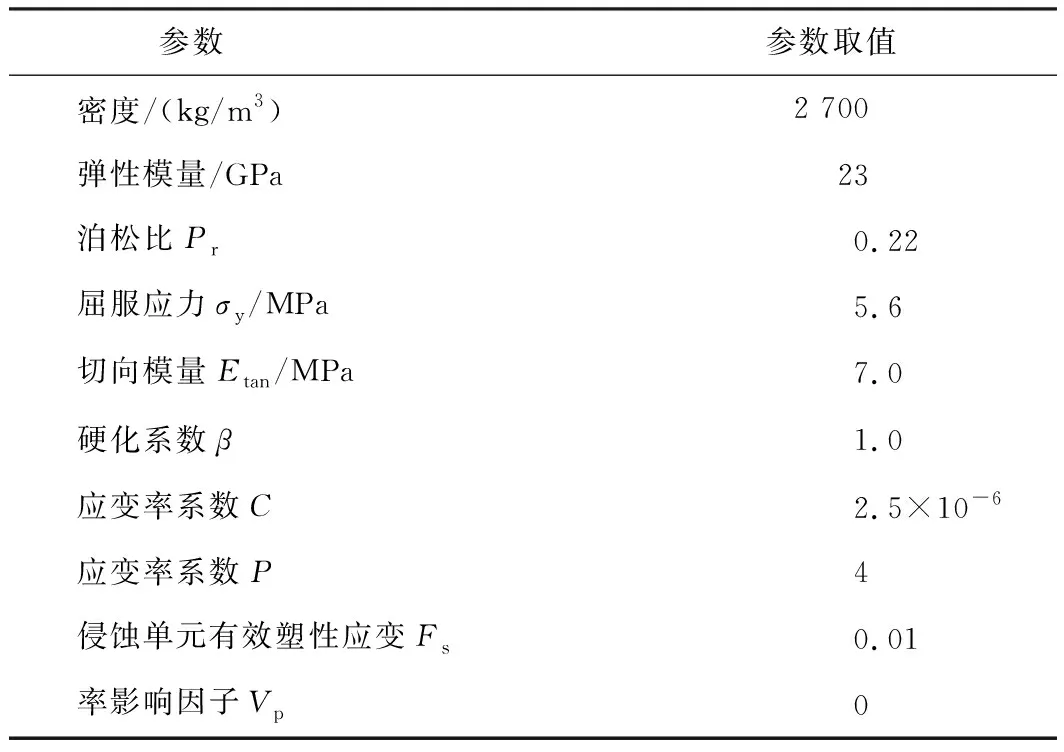
表4 围岩计算参数Table 4 Calculation parameters of surrounding rock

4 数值模拟结果

4.1 隧道内爆炸冲击波流场特征

取1/4模型进行详细说明，如图5所示。

图5 1/4模型图Fig. 5 Quarter numerical model

基于流固耦合模型再现了隧道内爆炸冲击波流传播过程，如图6所示。

爆炸前隧道内为标准大气压，压强约为0.1 MPa，如图6(a)所示；

如图6(b)—6(c)所示，随着爆炸发生，爆炸冲击波以球状向四周扩张，爆心处冲击波能量最强，压强高达226 MPa； 随着远离爆心，冲击波能量衰减极快，如靠近衬砌时的波阵面压强约为4.4 MPa，这是由于冲击波在扩大过程中，单位面积波阵面上的能量迅速减小，表明爆炸冲击波在自由空气中传播时能量衰减很快。

如图6(d)—6(e)所示，当爆炸冲击波首先作用于衬砌的拱顶与底板位置时，入射冲击波经反射形成反射冲击波，同时冲击波强度剧增，达到44.6 MPa。值得注意的是，曲边墙脚位置的爆心距最大，但该处的冲击波强度高达41.1 MPa，这是由于其“犄角结构”造成冲击波在此处反射效应最强。冲击波在与衬砌相互作用的过程中，由于隧道结构的不规则性，在衬砌表面形成的反射波传播轨迹各不相同，且不断循环并沿隧道纵向推进。例如，经拱顶反射的冲击波又以入射波作用于隧道底板。

图6 爆炸冲击波在隧道内传播特征 (单位： ×102 GPa)Fig. 6 Propagation characteristics of explosive shock wave in tunnel (unit: ×102 GPa)

此外，爆点附近形成一持续时间约6 ms的负压区域，如图6(f)—6(h)所示。形成此现象的原因是： 爆炸过程中TNT与空气燃烧形成向外膨胀做功的爆炸冲击波，待空气燃尽后由于无流体补充，故形成该负压区。随后经隧道衬砌反射的冲击波逐渐向爆心区域运动并最终汇合，同时负压区逐渐减小至消失，如图6(i)所示。冲击波汇合后继续沿各自轨迹运动，如图6(j)—6(l)所示，冲击波在隧道内无限不规则反射，使得隧道内压强长时间处于高压状态，加剧了对衬砌结构的破坏。

4.2 隧道冲击波强度特征

如图7所示，沿隧道纵向、径向分别布置若干测点。其中，沿径向测点为等间距分布，间距为1 m。基于流固耦合数值模型计算得到爆炸过程中各测点的超压时程曲线如图8所示，沿隧道纵、径向测点的超压峰值曲线如图9所示。

(a) 纵向测点位置 (b) 径向测点位置

(a) 纵向测点超压时程曲线

(b) 径向测点超压时程曲线图8 沿隧道纵、径向测点的超压时程曲线Fig. 8 Time-history curves of pressure of monitoring point along longitudinal and radial directions of tunnel

图9 沿隧道纵、径向测点超压峰值曲线Fig. 9 Curves of peak pressure of monitoring points along longitudinal and radial directions of tunnel

由图8可知： 爆炸发生后各测点处压强依次达到最大超压峰值，在衰减过程中又出现若干超压峰值，各测点的超压时程曲线表现出不同程度的振荡； 沿纵向分布测点的时程曲线较径向波动幅度更为明显，这是因为爆炸冲击波在沿纵向传播中反射效应更强； 爆炸过程中，在爆心附近区域形成的负压区如图8(a)所示； 沿隧道径向测点中，靠近曲边墙脚处的4#、5#、6#测点反射波的强度要高于入射波强度，位于曲边墙脚处的6#测点最为明显，如图8(b)所示。

从图9可清楚观测到爆炸冲击波强度并不随远离爆心而表现为衰减趋势。在靠近衬砌时冲击波强度明显增大，由于冲击波的多次反射，隧道内压强始终处于高压状态。这也从侧面解释了隧道内爆炸事故的巨大威力及所造成的严重后果。

4.3 数值计算结果与经验公式对比

前人基于坑道内的试验研究，通过拟合实测数据得到隧道内爆炸冲击波强度的预测公式(与比例距离相关)，如式(11)—(12)所示[1，21]。本节将数值计算结果与经验预测公式进行对比，结果如图10所示。

(11)

(12)

(13)

式(11)—(13)中： Δpm为爆炸冲击波超压峰值(波阵面压强减去标准大气压)，MPa；Z为比例爆炸距离，m/kg1/3；R为测点到爆心距离，m；W为TNT质量，kg。

由图10可知： 两经验公式均无法有效反映冲击波的反射效应，且都存在约束条件，主要体现在比例爆炸距离上，式(11)中0.656 m/kg1/3≤Z≤10.5 m/kg1/3和式(12)中Z>1 m/kg1/3，表明其无法对大当量爆炸即剧烈爆炸作用下爆心附近区域的冲击波强度进行有效预测与研究； 随着远离爆心，数值计算结果逐渐与经验公式吻合，但仍有不同，主要表现为经验公式一直呈衰减趋势，而数值计算得到的隧道内压强一直处于高压状态，如图中1 m/kg1/3≤Z≤1.4 m/kg1/3段。

图10 p-Z曲线结果与经验公式结果对比Fig. 10 Comparison between calculation results of p-Z curves of numerical simulation and empirical formula results

隧道为近似封闭的空间，隧道内爆炸冲击波流场较为复杂，作用在衬砌结构上的爆炸荷载也较难以用特定规律表征。而基于流固耦合效应的数值模型由于考虑了冲击波与衬砌之间的相互作用，可以较真实地再现隧道内冲进波流场及强度的变化特征。

4.4 隧道衬砌结构损伤特征

基于流固耦合模型数值模拟得到的隧道衬砌损伤特征如图11(a)—11(e)所示。可知： 衬砌拱部、曲边墙脚及底板中部先产生密集损伤裂缝，部分裂缝迅速贯穿形成局部破坏区，随后破坏区域、损伤裂缝分别自拱顶向两侧拱腰、自底板中心向两侧扩张至贯通，且同时沿隧道纵向发展，衬砌出现完全破坏区、严重破坏区及一般损伤区； 应力波自隧道底板传播至排水槽时，经反射由压缩变为拉伸，排水槽上部结构发生受拉破坏，隧道爆心附近的衬砌已完全破坏； 隧道曲边墙脚处已完全破坏，这与该处冲击波强度较高有直接关系。随着远离爆心，衬砌主要受损特征表现为遍布衬砌的损伤裂缝，主要以纵向裂缝为主，局部存在环向裂缝。通过与现场损伤调查情况(见图12)对比可知，衬砌损伤特征的数值模拟结果与现场情况基本一致，表明本文采用的研究方法适用于隧道内爆炸问题的研究。

4.5 隧道衬砌结构损伤机制

如图13所示，沿衬砌布设测点。每个断面布设9个测点，衬砌拱部沿隧道纵向共布设16个断面，监测点涵盖了衬砌拱部、曲边墙及隧道底板。提取各测点处最大、最小主应力峰值，根据LS-DYNA中“拉”正、“压”负原则，就衬砌损伤机制进行分析。

(a) 3.5 ms (b) 7.5 ms

(c) 10 ms (d) 20 ms

(e) 数值模拟结果图11 隧道衬砌结构损伤特征数值模拟Fig. 11 Numerical simulation models of lining damage characteristics

(a) 整体损伤特征

(b) 局部损伤特征图12 隧道损伤特征现场调查Fig. 12 Site surveying results of tunnel lining damage

(a) 横断面 (b) 纵断面

图13衬砌上测点分布
Fig. 13 Layout of monitoring points on lining

衬砌上主应力峰值曲线如图14所示。由图14可知： 作用于衬砌上拉应力峰值较高，约5 MPa，曲线的变化趋势较为平稳； 而压应力变化较大，介于13.4～99.8 MPa，主要与爆心距相关，爆心距5 m内衬砌受到压应力最大，此后随着远离爆心，压应力曲线逐渐趋于平稳。

图14 衬砌上主应力峰值曲线Fig. 14 Curves of peak principal stress of monitoring points on lining

结合图6、11及14，可知衬砌在爆炸冲击荷载下的受损机制为： 1)爆心距5 m范围内，衬砌在爆炸冲击波剧烈的冲压作用下形成局部破坏区，之后在冲击波拉、压交替作用下破坏区发展、贯通，直至形成完全破坏区； 2)由于爆炸冲击波在传播中能量逐渐衰减，作用于衬砌的压应力减小，但拉应力仍较高，衬砌上密集的损伤裂缝在较高压应力与拉应力共同作用下发展、扩张，致使爆心距5～10 m衬砌被切割成块状结构，丧失整体稳定性，形成严重受损区； 3)爆心距大于10 m的衬砌主要在较高拉应力作用下产生遍布衬砌的损伤裂缝，以纵向裂缝为主，局部有环向裂缝，形成一般损伤区。

5 结论与讨论

1)爆炸冲击波在隧道内传播经历了自由传播、规则反射及无规则反射传播状态。爆炸过程中爆心附近区域会出现负压区域，随冲击波传播会逐渐消失。冲击波在曲边墙脚处的反射最为剧烈，导致该处发生完全破坏，与其“犄角”结构相关。

2)由测点的超压时程曲线可知，沿隧道纵向冲击波反射作用更强。由冲击波强度峰值曲线可知，隧道内冲击波强度并无特定的衰减规律，靠近衬砌处，冲击波强度经反射后剧增，导致隧道内冲击波流场较为复杂，持续为高压状态。

3)相比较经验公式，流固耦合数值模型可有效反映冲击波的反射效应，且可对爆心附近区域的冲击波强度特征进行有效预测。

4)在剧烈爆炸作用下，爆心距5 m范围内的衬砌在冲击波冲压作用下发展形成完全破坏区； 爆心距5～10 m的衬砌在较高拉、压应力共同作用下形成严重破坏区； 爆心距大于10 m的衬砌在较高拉应力下形成一般损伤区。排水槽上方的隧道底板在冲击波的拉伸作用下发生受拉破坏。经对比，隧道衬砌损伤特征的数值模拟结果与现场损伤调查基本一致，验证了本文研究结果的可靠性，同时也佐证了本文建立的流固耦合数值模型可用于分析大型地下结构内爆炸动力响应问题。

本文研究还存在一些不足，仍有一些问题需要进一步探索，具体为：

1) 由于模型尺寸大，在协调好计算成本及误差控制下，单元网格尺寸还需进一步优化。

2) 由于瓦斯在隧道各部位积聚的不确定性，爆心位置或有多种可能。

3) 衬砌在实际施工中受到扰动存在一定的缺陷，后续研究中需考虑衬砌强度的折减。