压缩打捆机构及曲柄模态与谐响应分析

郭振华，陈换美

（1.石河子大学机械电气工程学院，石河子 832000；2.巴音郭楞职业技术学院）

0 引言

我国具有丰富的芦苇等粗纤维资源，可用于造纸、建材、饲料、医药等行业[1]。然而，由于芦苇密度低，致使其运输成本较高，愿意承担芦苇运输的车辆很少。芦苇打捆装备可以有效解决芦苇等原料运输过程中产生的亏吨问题，对降低企业生产成本具有非常重要的作用。但是，在打捆装备的工作过程中，机械振动不可避免。打捆机构在一定的振动频率范围内容易产生共振现象，这会导致关键构件发生结构损伤，进而影响对芦苇的压缩效果。本文针对打捆机的核心机构——压缩曲柄滑块机构及曲柄进行模态分析和谐响应分析，为打捆机的设计提供理论参考。

1 模态分析理论

模态分析是将系统的振动微分方程组中的物理坐标变换为模态坐标，通过方程组解耦，求出系统的模态参数，使其成为用模态坐标和模态参数描述的独立方程[2]。

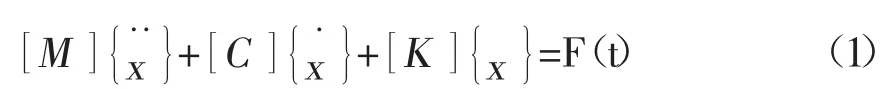
式（1）为N自由度的线性振动表达式。式中 [M]——系统的质量矩阵；[C]——系统的阻尼矩阵；[K]——系统的刚性矩阵；——系统加速度——速度；x ——位移；F（t）——系统激振力。

模态分析分为自由模态分析和约束模态分析。自由模态是指在不考虑任何约束的情况下，得到的系统本身固有特性。自由模态是模态分析的重要组成部分，通过自由模态分析，可以对系统自身的尺寸、材料、振动等固有特性有必要了解。约束模态则是指系统在受约束情况下的模态分析[2]。

对系统进行自由模态分析时，设定系统在振动时不受外力，即 F（t）=0。此时，系统内部阻尼较小，在分析系统自由振动的频率和振型时可忽略不计。得到系统无阻尼振动微分方程：

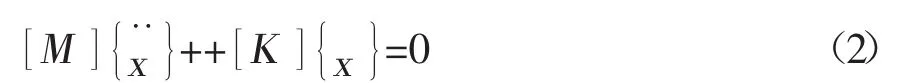
该方程特解为：

式（3）中，Φ表示自由响应幅值矩阵。

将式（3）代入式（2）中，可得特征方程：

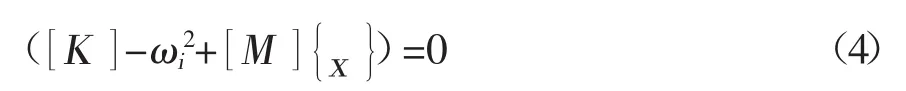
式（4）中，ωi表示第 i阶固有频率。

经过上述变换，将系统固有频率和振型问题转变成求解方程特征值问题。方程（4）有非零解的充要条件为：

应用分块兰索斯法（Block Lanczos）将方程（5）变换为对角矩阵，采用追赶法求解，可得n个不同正解ωoi（i=1，2,…n）。

ωoi表示系统第i阶固有频率。

2 压缩曲柄滑块机构模态仿真分析

偏置式曲柄滑块机构是压缩打捆机核心部件，该部件的刚度、强度及其力学特性决定整机的使用寿命。通过对打捆机曲柄滑块机构进行有限元模态分析，得出其在工作状态下的固有频率和振型，可以为避免共振现象的产生提供数据支持。

2.1 建立有限元模型

有限元分析软件abaqus自带三维建模功能，但是建模过程繁琐，并且精度较低。为提高建模效率，应用专业三维建模软件solidworks对压缩曲柄滑块机构进行建模，然后将建好的三维模型导入abaqus中进行分析。建模过程中，为减少计算时间提高分析效率，可以在不影响分析效果的前提下对模型进行简化，如：忽略圆角倒角等对有限元分析结果影响不大的结构特征。

具体步骤如下：

（1）应用三维软件建立打捆机曲柄滑块机构的三维模型；

（2）将建成的三维模型另存为Para solid格式，并导入abaqus软件中；

（3）在abaqus环境下设置模型材料，具体设置如表1所示：

表1 40Cr材料属性

（4）划分网格：网格划分类型采用0.008 mm四面体，结果如图1。

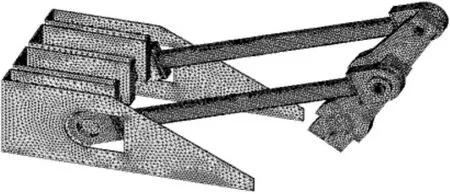
图1 压缩曲柄滑块机构的网格划分图

（5）对网格划分结果进行检测，结果如表2，表明网格划分结果满足模态分析要求。

表2 材料属性

2.2 仿真结果及分析

模态分析提取阶数设置为5阶，扩展阶数设置为5阶，频率区间设置为0～3 000 Hz。

在上述参数设置下，对曲柄滑块机构进行约束模态分析，仿真结果如下：

前5阶固有频率和振型描述如表3所示：

分析结果可知：

（1）在前5阶模态仿真结果中，1阶模态和2阶模态固有频率为为0或近似为0，可认为结构基本无变形，表现为刚性。

（2）3阶至5阶的模态云图表明，曲柄滑块机构发生明显的变形和位移。其中，曲柄的变形较明显，故对曲柄进行单独的模态分析。

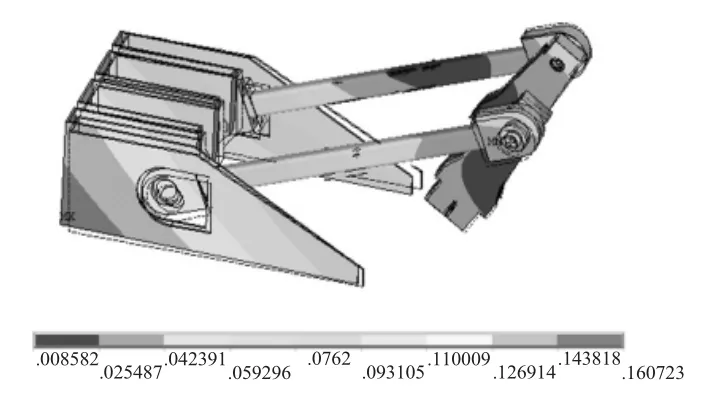
图2 模态云图第3阶

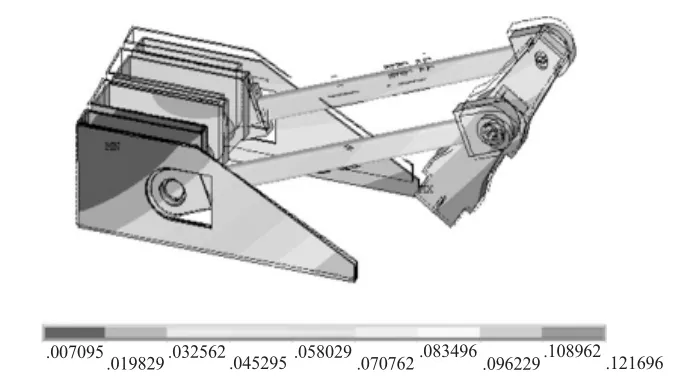
图3 模态振型云图第4阶

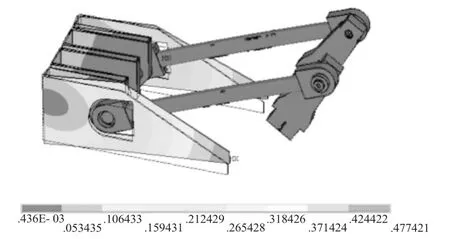
图4 模态振型云图第5阶

表3 前5阶固有频率和振型描述

3 压缩曲柄的模态仿真分析

通过对曲柄进行网格划分和模态分析，得到曲柄的5阶约束模态云图，结果如图5至图9所示：

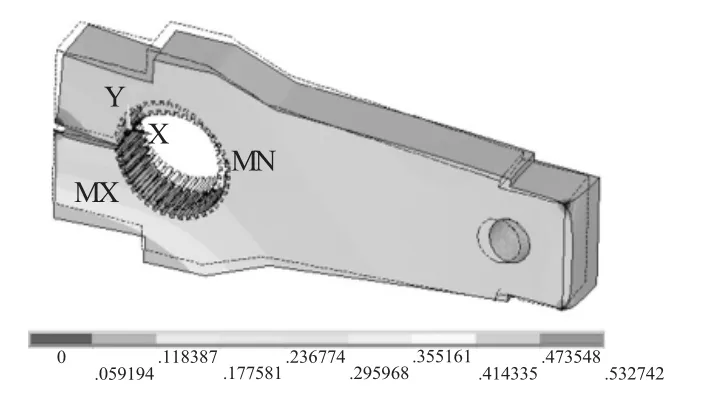
图5 模态云图第1阶

曲柄的5阶模态分析云图描述如表4。

通过上述分析可知，曲柄的5阶模态固有频率分别为 6.71Hz、19.68Hz、28.89Hz、116.73Hz、255.63Hz。为避免共振现象的发生，在打捆机工作状态下，应避免出现上述频率。

打捆机的工作频率可由式（7）表达。

式中 f——激振频率；n——动力输出轴转速；δ——误差系数。

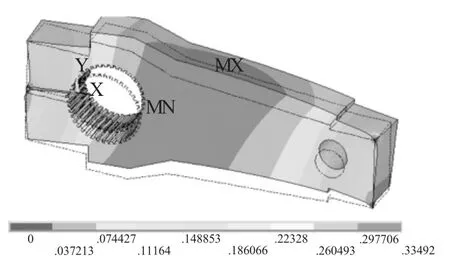
图6 模态云图第2阶

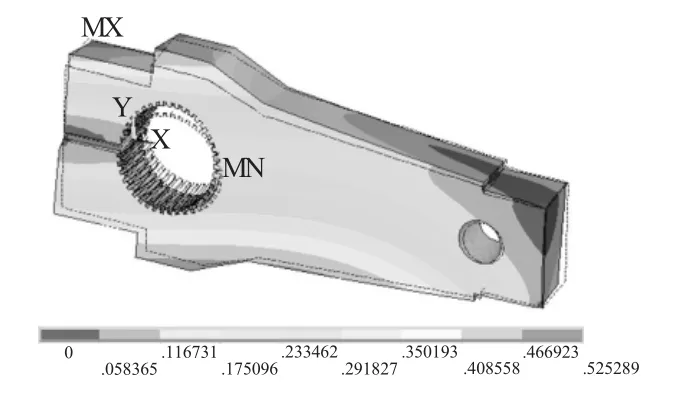
图7 模态云图第3阶

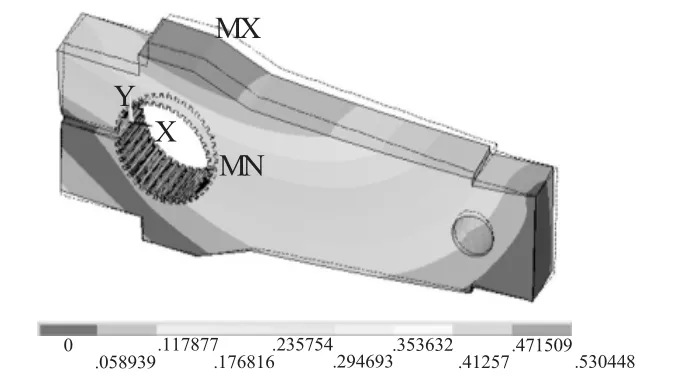
图8 模态云图第4阶

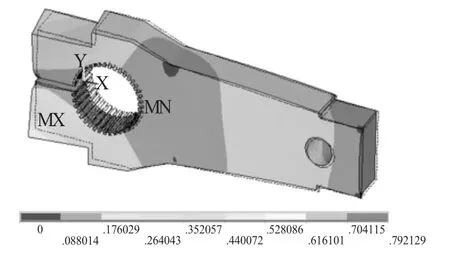
图9 模态云图第5阶

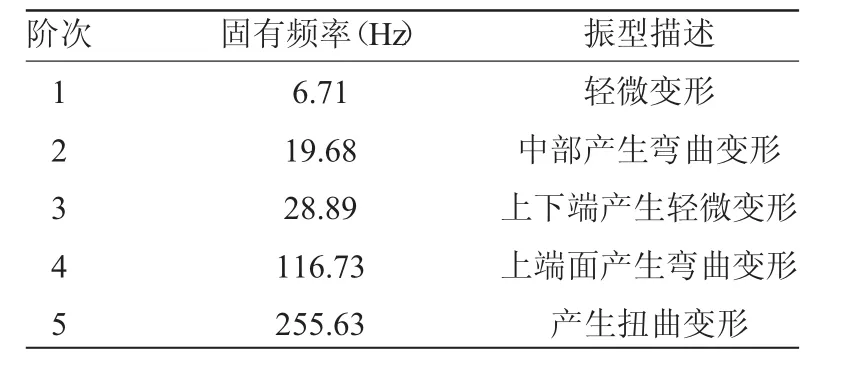
表4 曲柄前5阶模态描述

通过式（7）可求得不同频率下对应的输出轴转速，如表5所示。

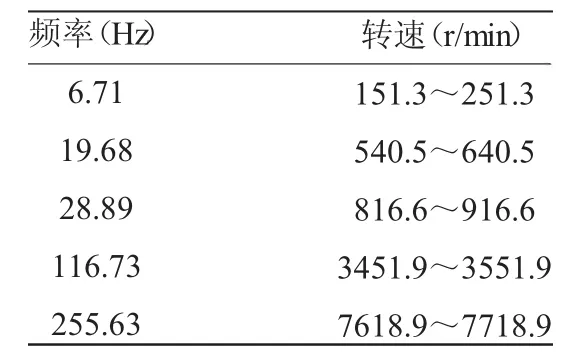
表5 转速对应表

根据国家标准，拖拉机动力输出轴转速范围为540～1 000 r/min。对应表5，为避免共振现象的产生，发动机转速应尽量避免540.5～640.5 r/min和816.6～916.6 r/min两个转速范围内使用。

4 谐响应分析

谐响应分析用于确定线性结构在承受随时间按正弦（简谐）规律变化的载荷时的稳态响应，分析过程中只计算结构的稳态受迫振动，不考虑激振开始时的瞬态振动。谐响应分析的目的在于计算出结构在几种频率下的响应值对频率的曲线，从而能预测结构的持续性动力特性，验证设计是否能克服共振、疲劳以及其他受迫振动引起的有害效果[2,6,8]。压缩打捆机曲柄的模态分析反映了系统本身的振动属性，谐响应分析可以反映其在实际工作环境下的振动响应。

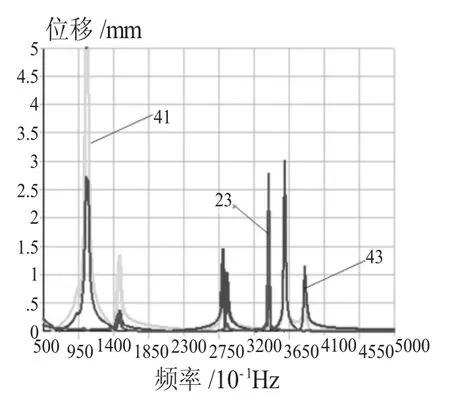
图10 Y平面内谐响应分析云图

4.1 谐响应参数设置

通过模态分析可以得到压缩曲柄滑块机构曲柄的固有频率范围为0～256 Hz，因此，选取0～500 Hz为机构的激振范围，设置载荷步为200，在曲柄端施加幅值为3000N的简谐载荷。根据所得的约束模态振型，提取3处关键点进行响应分析，分别取机构中关键点23、41、43。关键点的位移响应如图10和图11所示。

4.2 仿真结果及分析

通过对响应云图10和图11的分析可知：当振动频率为100.81Hz、126.11Hz、278.6Hz、321.93Hz（舍去）、350.35Hz（舍去）时，曲柄易发生共振现象。其中，最大谐峰值出现在第4阶和第5阶。可见，在压缩打捆机工作过程中，不同的振动频率将会产生不同振幅，振幅过大会影响压缩效果，甚至对设备造成一定的破坏。

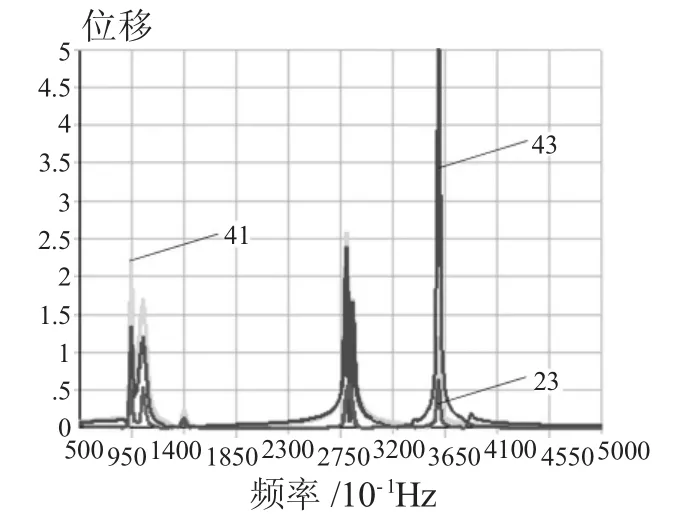
图11 Z平面内谐响应分析云图

5 小结

本文通过对压缩打捆机曲柄滑块机构及曲柄进行模态分析和谐响应分析得到以下结论：

（1）曲柄滑块机构的前5阶模态中，1阶和2阶模态表现为刚性，3阶至5阶模态中曲柄滑块机构表现出明显的位移和变形，其中曲柄表现较明显。

（2）曲柄的5阶模态固有频率分别为6.71 Hz、19.68 Hz、28.89 Hz、116.73 Hz、255.63 Hz，在固有频率下曲柄的上下端面易发生变形，5阶模态下发生扭曲变形。为避免共振现象的产生，发动机转速应避免在 540.5～640.5 r/min和 816.6～916.6 r/min两个转速范围内使用。

（3）谐响应分析表明，当振动频率为100.81 Hz、126.11 Hz、278.6 Hz时，曲柄将发生共振现象。其中，最大谐峰值出现在第4阶和第5阶。