离散切换系统的事件触发输出调节：相邻模态依赖平均驻留时间

李莉莉，郭家珺，宋林阳

切换系统通常由一系列连续或离散的子系统和协调子系统之间如何切换的切换规则组成.它具有广泛的实际应用背景，如一些工业过程和智能运输系统［1］.切换规则设计方法主要有多Lyapunov函数方法、平均驻留时间方法和模态依赖平均驻留时间方法［2］等.王月娥［3］提出了相邻模型依赖平均驻留时间方法（AMDADT），它将同一个子系统按由哪个子系统切换而来进行分类，这使得每个子系统的平均驻留时间不仅与当前子系统有关，而且与其前一个运行的子系统相关.另一方面，输出调节问题是控制理论中非常热门的话题［4］.它的目的是设计一个控制律，使系统的输出误差渐近趋于零，消除外部扰动的影响.Li J［5］设计了仅依赖于输出误差信息设计切换规则和控制器，通过构造非共同坐标变换，给出了线性离散切换系统的输出调节问题可解的充分性条件.事件触发控制仅在满足特定的触发条件时更新控制器的信息，否则，保持原控制信息不变，这样可以降低控制器的更新频率，从而达到节约资源的目的.此外，还可通过改进事件触发机制来达到这个目的.

本文研究一类线性离散切换系统在事件触发控制下的输出调节问题.首先，把连续切换系统的AMDADT的定义拓展到了离散切换系统上.与现有的驻留时间方法不同，本文所使用的子系统的平均驻留时间不但与该子系统有关，而且还与其前一个运行的子系统有关，也因此得到了满足AMDADT条件的切换规则.通过联合设计基于系统状态的控制器和事件触发机制，得到该切换系统输出调节问题可解的充分条件.最后，通过数值示例验证本文方法的有效性.

1 问题描述与预备知识

1.1 问题描述

考虑如下线性离散切换系统

其中，x(k)∈Rn是系统的状态，u(k)∈Rm是控制输入，e(k)∈Rm是输出误差，ω(k)∈Rr表示外部扰动.Ai,Bi,Ci,Di,Ei和Si(i∈M)是具有适当维数的矩阵.σ(k):Z+→M={1,2,…,m}是切换信号.设系统的初始点为k0=0，系统在初始点驻留在子系统i0上，i0∈M.在切换信号σ(k)的作用下，不失一般性，令系统按以下切换序列Σ:{(i0,k0),…,(ij,kj),…|ij∈M,j=0,1,… 切换，并用r1,r2,…,ri,ri+1,…}表示事件触发的离散时刻.

假设1 矩阵Si,i∈M所有特征值的模都大于等于1.

注：假设1在切换系统输出调节问题中是一个标准的假设.

当一个事件发生时，事件触发机制会把最新的状态信息更新到控制器中，构造如下全息状态反馈事件触发控制器

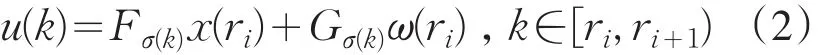
其中，Fi，Gi(i∈M)是待设计的适当维数矩阵.对于切换系统（1），应用事件触发控制器（2），如果满足了事件触发机制的条件，那么控制器刷新.事件触发机制将会在定理的证明中给出.

1.2 预备知识

定义1 对于切换系统（1），设计形式如（2）的控制器和一个切换规则σ(k)使得：a.当扰动ω(k)=0时，系统（1）和控制器（2）构成的闭环系统在事件触发机制下和切换规则σ(k)下渐近稳定.b.对每个 (x(0),ω(0))，方程

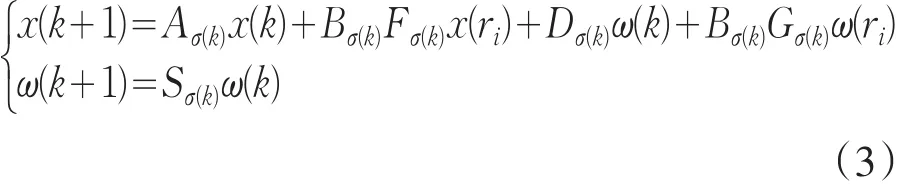
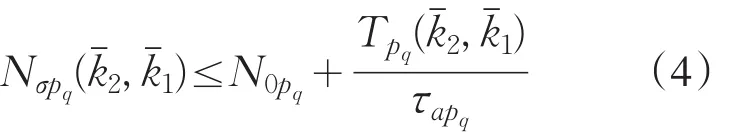
成立，那么就称切换信号σ(t)具有相邻模型依赖平均驻留时间τapq，N0pq代表了相邻模型依赖的抖振界.其中，p，q∈M ，q≠p，pq代表子系统p，但是子系统p是由子系统q切换来的.

引理1 对于任意带有适当维数的矩阵X，Y，下面的不等式成立 XTY+YTX≤XTX+YTY.

2 主要结果

本节基于系统状态和外部输入信息可完全获知的条件下，解决系统（1）和控制器（2）在事件触发机制下的输出调节问题.

定理1 考虑切换系统（1），并令其外部系统满足假设1，如果

1）对∀p,q∈M(p≠q)，存在Πp，Πq，Fp和Gp，满足

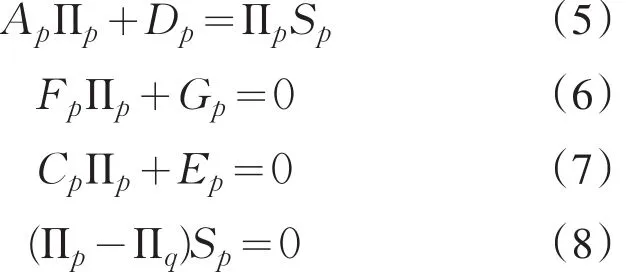
2）对给定的0＜λqp＜1，0＜≤1和＞0 ，若存在＞0，使得矩阵不等式组

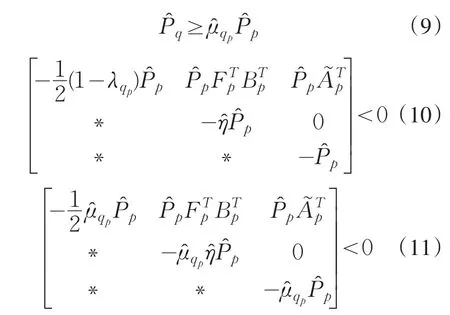
成立，则存在全息反馈控制器（2）和事件出触发机制，使系统（1）在满足相邻模态依赖平均驻留时间

的任意切换信号下，事件触发状态反馈控制器（2）和事件触发机制（15）可解决切换系统（1）的输 出 调 节 问 题 ，其 中

不失一般性，假设当 σ(k)=p≠σ(k+1)=q时 ，由（5）、（6）和（8）能 够 得 出，再 由（7）能 求 得 e(k)=，所以闭环系统可重写为

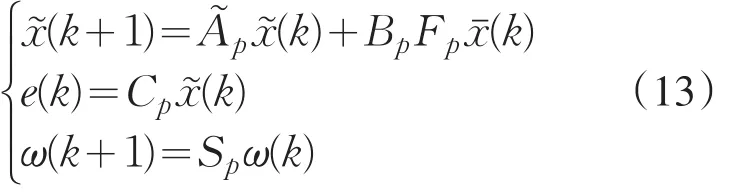
选取如下形式的Lyapunov函数

当 σ(k)= σ(k+1)=p 时，Vp(x͂(k+1))-(1-λqp)Vp(x͂(k))=，运用引理1可得

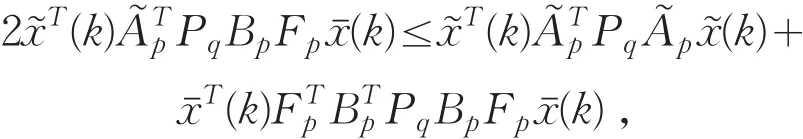
这时，设计如下形式的事件触发机制

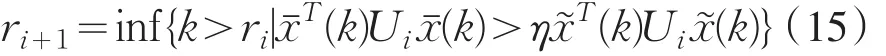
再由事件触发机制（15）可知

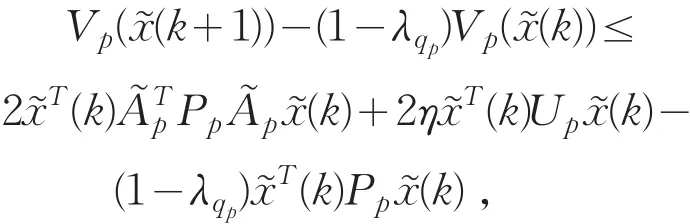
此时，对（10）式用两次Schur补引理可得

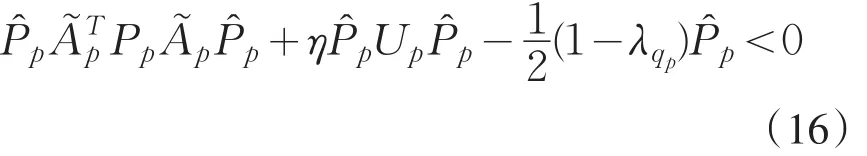
再对（16）式两端，同乘 Pp得

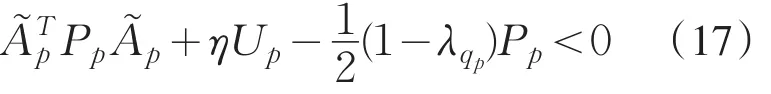
于是，可以得到

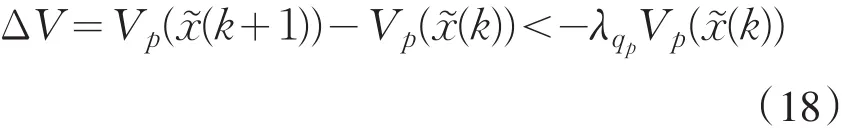
这意味着Vp(x͂(k))沿着各子系统的轨迹是下降的.

当 σ(k)=p≠ σ(k+1)=q 时 ，Vq(x͂(k+1))-， 对 此 式用引理 1，由（9）可得 Pq≤μqpPp，并 由 此 可 以 得 到

再由事件触发机制（15）得

采用处理（10）的方法，处理（11）可得

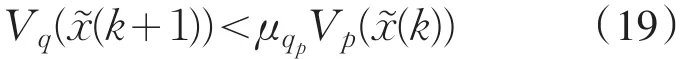
令相邻模型依赖抖振界 N0pq=0，则对∀k＞0，取k0=0，并令 k∈[ki,ki+1)，那么在区间[ki,k]，由（18），可得

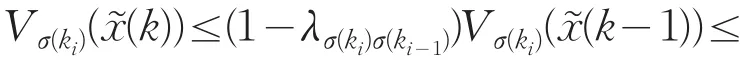
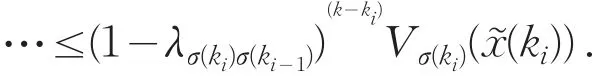
再由（19）可以得到

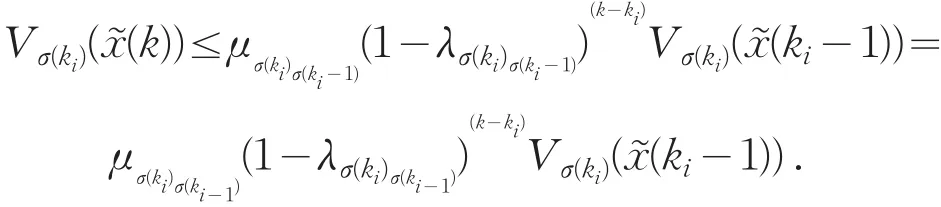
以此类推，可以得到

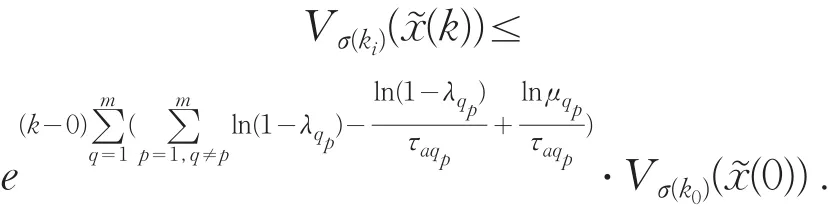
于是，无扰动输入时，系统（13）在满足AMDADT（12）的任意切换信号下是渐近稳定的.同时，可以得到

3 数值算例

考虑含有两个子系统的切换系统（1），其中

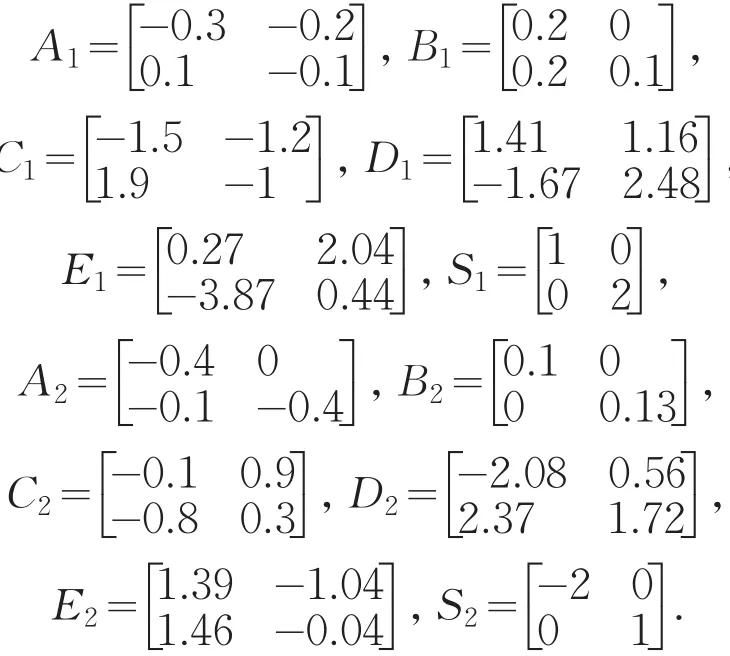
求解满足定理1中1）的未知矩阵如下

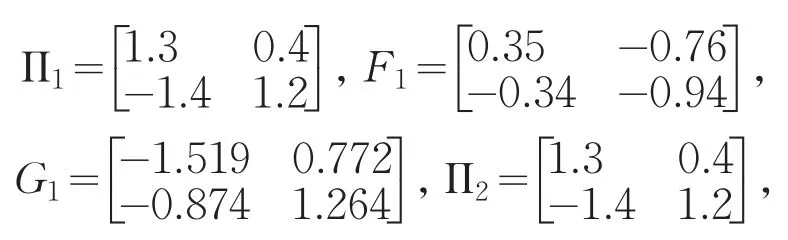
取参数 μ12=1.2，μ21=1.1，λ12=0.6，λ21=0.55，η=0.25.应用线性矩阵不等式可以求得

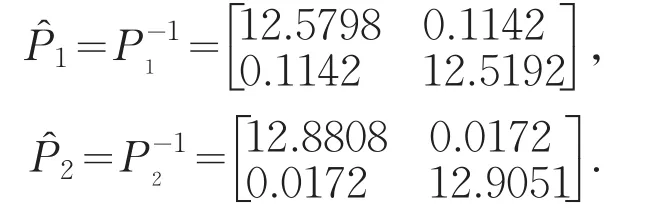
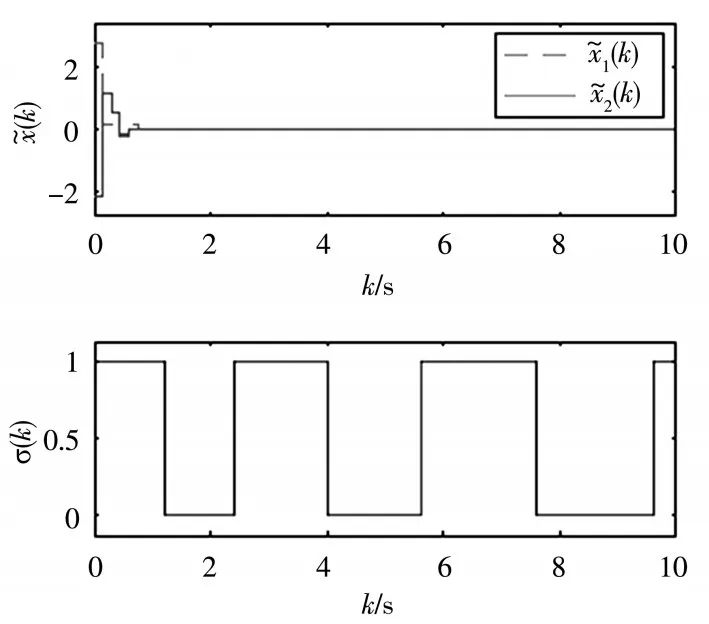
图1 闭环系统状态和切换信号

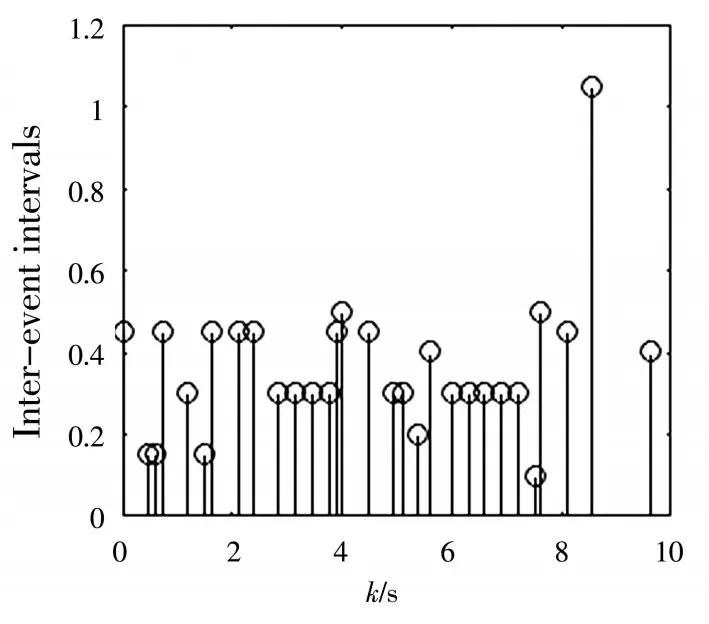
图2 事件触发间隔

图3 系统的输出误差和输入

4 结论

本文用相邻模态依赖平均驻留时间方法，研究了一类线性离散切换系统在事件触发全息状态反馈控制器作用下输出调节问题.对事件触发机制及控制器联合设计，利用分段Lyapunov函数方法和AMDADT给出了事件触发机制和切换规则共同存在的条件.并给出在一类AMDADT切换信号下，该切换系统输出调节问题可解的充分条件.最后，通过Matlab仿真验证了在切换系统事件触发输出调节问题可解前提下，控制器更新频率明显降低，验证了结论的有效性.