考虑流道和轮盘结构的多级低压涡轮多学科优化方法研究
龙 丹 ,郭福水 ,罗 钜 ,赵 磊 ,陈辉煌 ,闫 成
(中国航发商用航空发动机有限责任公司a.设计研发中心;b.上海商用飞机发动机工程技术研究中心,上海200241)
1 引言
现代民用航空发动机涵道比的不断增大,以及低压转速受风扇强度和噪声指标的限制,为满足风扇功率和涡轮效率的需求,必须采用多级低压涡轮设计[1]。航空发动机涡轮在设计过程中涉及众多耦合学科,包括气动、传热、结构、强度、寿命和振动等。但传统设计方法设计周期较长,成本较高,且只能得到基本满足各学科要求或相对较好的方案,很难得到整体最优方案[2]。
为改善传统设计方法弊端,多学科设计优化(MDO)方法应运而生,并开始应用于航空发动机领域[3-5],这其中以对涡轮MDO的研究最为广泛。国外,Talya等[6]建立了一个综合考虑气动、传热、结构和模态设计等的通用三维叶片的多学科优化模型,在满足气动、结构、模态和几何约束下,使得叶片的温度最低、质量最轻;Salnikov[7]以单级高压涡轮叶盘为研究对象,在考虑结构、传热、强度和寿命等学科下对其进行了优化;Marchukov等[8]针对三级低压涡轮叶片进行多目标多学科优化,得到了满足气动和强度准则的最优构型。国内,吴立强等[9]综合考虑结构、气动、传热、强度、振动和寿命等多个学科,对涡轮叶片进行了优化;王婧超等[10]建立了全三维涡轮叶片的一体化MDO系统,涉及气动、结构、强度、振动等多个学科,有效提高了涡轮叶片性能;周莹舻[11]针对带气冷叶片的涡轮叶盘整体结构进行MDO研究,实现了带气冷叶片的涡轮叶盘流热耦合设计优化;申秀丽等[12]研究了基于涡轮流道的多学科优化方法,使涡轮气动和结构强度的多学科综合性能大大提高。这些研究均展现了MDO在航空发动机设计中的应用前景,但其主要研究对象是涡轮叶片、叶盘或单级涡轮。截至目前,国内针对多级低压涡轮MDO的研究相对较少。
相对于单级涡轮,多级低压涡轮MDO存在设计参数多、耦合作用强、计算时间长等难点。为缩短优化时间、提高多级低压涡轮设计水平,十分有必要进一步研究针对多级低压涡轮的MDO方法。为此,本文通过分析多级低压涡轮的设计特点,综合考虑低压涡轮气动、结构、强度和寿命等学科,并通过探索不同学科间的耦合协调机制,建立了多级低压涡轮MDO系统。同时,为提高优化效率,还采用试验设计方法对关键设计参数进行了筛选。最后,基于NSGA-II算法对某型发动机的6级低压涡轮部件进行了多学科优化研究。
2 学科分析模型
2.1 气动分析模型
采用一维气动设计方法[13-14]建立气动分析模型。根据工程设计经验,涡轮一维设计时的气动设计输入参数主要包括以下两部分:
(1)发动机总体设计对低压涡轮提出的设计要求,包括涡轮进口流量、进口总压、进口总温、功率、转速及流道尺寸等。在气动优化过程中,主要作为输入参数或约束变量。
(2) 低压涡轮的气动设计参数,包括级数、各级功分配、反力度、各叶片排轴向长度、轴向间隙及进出口流道尺寸等。这些参数一般由涡轮气动设计人员根据设计经验,并结合现有设计基础给出,可将其设置为优化的设计变量。特别地,由于进口流道尺寸受级间机匣设计的限制,而级数和出口流道外径则主要根据总体性能设计指标(效率、功率、膨胀比和质量等)和部件设计水平来综合确定,在优化中保持不变。
低压涡轮气动设计参数的选取还需综合考虑多方面的限制要求。首先,出口马赫数不宜设计得过大或过小。涡轮出口马赫数过大会增加气流损失;过小会使得流通面积变大,叶片变长,导致涡轮质量增加,叶片强度降低。其次,叶片数的选择应兼顾涡轮质量和气动效率的影响,减少叶片数可减轻涡轮质量,但会提高单个涡轮叶片的负荷水平,而负荷过大可能会增加叶栅流动损失,降低涡轮气动效率。最后,涡轮出口气流角也应限制在接近轴向的一定范围内。
通过一维气动设计的低压涡轮气动一维流道如图1所示,图中蓝色表示静叶,红色表示动叶。该低压涡轮共6级。
2.2 强度分析模型
根据低压涡轮设计流程,完成气动设计后进行结构强度分析。在气动一维设计的基础上,涡轮叶片采用AN2(转子叶片出口环形面积与转速平方的乘积)进行叶根应力评估,将叶片简化成等效质量点加载于盘缘,进行多级涡轮盘静强度、破裂裕度和寿命分析。同时,由于各级轮盘间的耦合作用,因此需要同时建模与分析。
采用ANSYS有限元方法对多级低压涡轮强度进行分析。假设优化前后各零件使用的材料不变,在初始设计条件下进行热分析得到低压涡轮盘温度场,并加载至强度分析模型。
为保证低压涡轮安全可靠运转,设计中应满足相应强度要求。轮盘静强度分析时主要考核各级轮盘的最大径向应力和最大周向应力。根据《航空涡喷、涡扇发动机结构设计准则》[15],采用安全系数评估静强度,采用平均应力法评估破裂转速裕度[16-17],采用基于材料S-N曲线的名义应力法进行低周疲劳寿命分析。安全系数和破裂转速裕度计算公式分别如式(1)和式(2)所示,其具体数值根据工程经验及相关强度准则确定。
式中:nxm为径向应力安全系数,σ0.1为对应材料的屈服强度,σmax为每个盘的最大径向应力/周向应力,Sxbm为径向破裂裕度,ε为材料系数,σb为拉伸强度,σavg为平均周向应力/径向应力。
3 多级低压涡轮MDO方法
低压涡轮设计过程中,气动与强度学科相互耦合最为密切。一方面,气动设计得到的流道和叶片直接决定了轮盘的尺寸和受载,进而影响轮盘的强度和质量。另一方面,随着航空发动机设计水平的不断提高,涡轮温度和转速越来越高,叶片或轮盘的强度往往也会制约气动设计,迫使气动重新进行设计,并与强度反复迭代。特别地,当低压涡轮级数增加时,由于设计参数的数目成倍增加,且级间性能相互影响,这种耦合作用更为突出。
针对低压涡轮这一典型多学科耦合设计问题,本文建立了多级低压涡轮MDO流程,如图2所示。具体实现过程如下:
(1)基于现有各学科设计参数进行灵敏度分析,筛选关键设计变量;
(2)基于自编程序执行一维气动计算;
(3)采用UG软件对结构参数化建模,执行自编模型更新程序;
(4)执行基于Hypermesh Tcl语言的自动化分网程序,建立对应结构的有限元模型;
(5)执行强度自动化分析程序,进行静强度计算、破裂裕度分析及寿命估算;
(6) 根据分析结果,判断是否满足约束条件,目标函数是否最优,否则调整设计参数重新迭代计算。
该流程充分考虑了气动设计与结构强度设计的耦合作用,及多级低压涡轮级间参数的相互影响,采用了科学的灵敏度技术、先进的优化方法及高效的优化算法,使设计过程不断在气动与强度中迭代,并以多级低压涡轮气动和强度设计多目标为牵引,在提高低压涡轮综合性能的同时,大大缩短了设计周期。
3.1 参数灵敏度分析
对于6级低压涡轮,共有77个气动设计参数及489个结构尺寸参数。为兼顾优化效率和优化效果,采用试验设计方法进行参数灵敏度分析,筛选所有参数中对约束条件或目标影响较大的关键参数,并设置为优化中的设计变量。
根据灵敏度分析结果,功分配系数FC、运动反力度Ω、流道控制点Cp对气动约束条件和气动效率影响较大,Cp与叶片排轴向长度系数Axl等对子午流道影响较大,涡轮盘盘心厚度Wb、涡轮盘辐板厚度Wr、涡轮盘心高度Hr和涡轮盘内径R等4个尺寸参数对轮盘质量、应力安全系数和破裂裕度影响较大。图3、图4分别示出了各设计参数对气动效率和径向应力安全系数的影响。图中,G为叶片排轴向间隙系数,红色表示该参数对目标产生负影响,蓝色表示正影响,数值越大表示灵敏度越高,各参数后的数字表示级数;下标s表示静叶,r表示动叶,t表示叶尖,b表示叶根,如Axl1表示第一级动叶轴向长度系数。
3.2 优化模型建立
涡轮优化数学模型建立的主要内容为,选取目标函数、设置约束条件及定义设计变量等。目标函数的选取应充分考虑多学科的设计指标。气动设计中,效率是衡量气动设计好坏的重要标准。而结构强度设计时,在满足强度设计要求下,质量最轻是结构设计的最终目标。因此,选取质量和气动效率为目标函数,进行多目标优化。低压涡轮的设计需要满足多方面的设计要求,约束条件即是这些设计要求的具体体现。通过合理约束设计变量,保证优化结果能满足涡轮气动、结构、强度及寿命等设计要求。根据3.1节参数分析结果,将筛选得到的关键参数FC、Ω 、Cp、Axl、Wb、Wr、Hr和R,定义为优化中的设计变量。
根据上述分析,低压涡轮多学科优化模型可表述为:
式中:η为气动效率,W为低压涡轮总质量,β为出口气流角,Ma为出口马赫数,Zw为各级升力系数,Nf为低周疲劳寿命,nzm为周向应力安全系数,Szbm为周向破裂裕度,αr为各级动叶转折角,αs为各级导叶转折角,i=2,3…n,j=1,2…n,n为低压涡轮级数,k=1,2,b1~b10为相应参数的约束上下限。
3.3 优化求解
根据上述多学科分析模型和优化数学模型,以某型发动机低压涡轮为原始设计模型,在Isight优化软件集成并进行多学科优化。优化算法选用NSGA-II算法[19-20]。
4 结果分析
多级低压涡轮多学科优化运行1 280步后收敛,共耗费26 h。优化过程中气动效率和质量变化历程分别如图5、图6所示。优化过程中共得到995个可行解,其中有15个Pareto解,其分布如图7所示。
为便于数据对比,对优化数据进行了标准化处理:
式中:X′为标准值,X为真实值,X0为初始值。
由图可见,多目标优化算法NSGA-Ⅱ有助于设计者进行多方案对比,实现先优化后决策。文中分别以气动效率最高、涡轮质量最轻和综合评价函数最小为最优评价指标,不同评价指标下目标函数在优化前后的变化如表1所示。表中,F为综合评价函数[21],其计算公式为:
式中:ω1和ω2为权重系数,可根据工程实际需要确定,本文均设置为0.5;W0为涡轮初始质量。
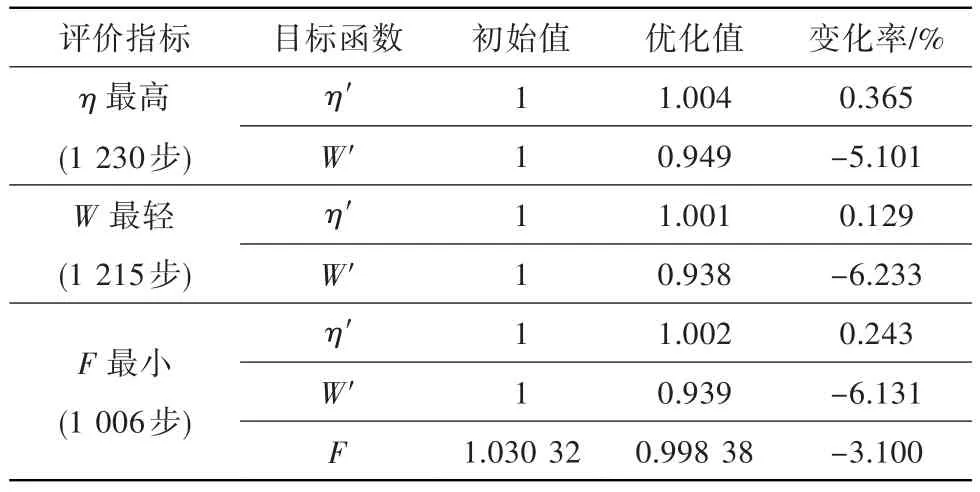
表1 优化前后目标函数的变化Table 1 Comparison of objectives functions before and after optimization
由表中可见,不同评价指标下得到的最优解均不相同。当以气动效率最高为最优评价指标时,最优解出现在第1 230步,优化后气动效率增大0.365%,质量下降了5.101%;当以质量最轻为最优评价指标时,最优解出现在第1 215步,优化后气动效率增大0.129%,质量下降了6.233%;而当以综合评价函数最小为最优评价指标时,最优解出现在第1 006步,优化后气动效率增大0.243%,质量下降了6.131%,综合评价函数降低3.100%。
根据工程设计经验,下文以综合评价函数最小为最优评价指标,来分析优化前后设计变量和约束条件的变化规律。图8、图9分别为优化前后部分设计变量和约束条件的对比,图10、图11分别为优化前后低压涡轮流道和低压涡轮5级盘结构对比。
由图8可见,优化后各设计变量均有较大幅度的变化,正是通过优化过程中各个设计变量取值的不断调整,得到了气动效率更高而结构质量更轻的设计方案。
在进行多级低压涡轮优化时,各级间的设计参数相互影响,特别是气动设计参数。以Axl为例,由于低压涡轮轴向总长为总体性能给低压涡轮气动设计提出的设计边界条件,在优化中保持不变,因此优化后呈现此消彼长的变化趋势。当第1、第5级动叶和第2、第4、第6级静叶轴向长度增大时,其他级动叶和静叶轴向长度会减小。同样的变化趋势也可在图10中看出,且优化后低压涡轮流道较优化前更为平缓。
在结构上,各级结构设计变量的变化相对一致,且均朝着低压涡轮质量减小的目标变化。与此同时,各级强度指标均满足相应的强度准则。应当指出的是,由于初始状态轮盘寿命远大于寿命下限,因此优化后轮盘寿命依然满足设计要求。
特别地,对于个别强度约束,如nxm和Sxbm,优化后裕度反而更大。这是因为在其他因素保持不变的情况下,单级轮盘质量降低的同时会降低相邻轮盘的负荷,从而获取更大的减重空间,这进一步说明了多级低压涡轮协同优化的优越性。
5 结论
通过分析多级低压涡轮设计特点,考虑低压涡轮气动、结构、强度和寿命等学科,研究了针对多级低压涡轮的MDO方法,建立了多级低压涡轮多学科优化流程,并针对某型发动机6级低压涡轮,以气动效率最高和结构质量最轻为多目标,采用NSGA-Ⅱ算法进行多学科优化设计,得到以下结论:
(1)优化共得到15个Pareto解,在不同的最优评价指标下,得到的最优解均不相同。
(2)为兼顾多目标优化效果,以综合评价函数最小为最优评价指标,在满足气动和强度约束的条件下,优化后低压涡轮气动效率增大0.243%,整体质量下降了6.131%,综合评价函数降低3.100%,优化效果明显,说明了进行多级低压涡轮多目标多学科优化的重要性。
(3)在其他因素保持不变的情况下,单级轮盘质量降低的同时会降低相邻轮盘的负荷,从而获取更大的减重空间,这进一步说明了多级低压涡轮协同优化的优越性。
(4)本文所建立的多级低压涡轮多学科优化模型中,目前主要考虑了气动、结构、强度和寿命等学科,还可进一步开展包含传热、噪声和振动等其他学科的多学科优化方法研究,以便更好地应用于工程。

