力学课程一题多解对学生创新思维能力的培养探索

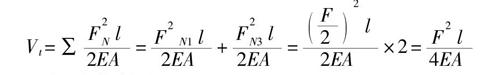
【摘 要】力学课程是工科院系的一门专业必修课程，它的理论体系、思维方法都很严密，系统性强，学生的用不同的定理、定律、方法，使学生学会不同角度的研究方法，得出不同层面的信息，以启发、培养学生的创新意识。实践证明，适时的运用这种方法，有效增强了学生思维的灵活性和开拓性。

【关键词】力学课程;创新思维;能力培养

中图分类号： G642;TB301-4 文献标识码： A 文章编号： 2095-2457（2019）35-0117-002

DOI：10.19694/j.cnki.issn2095-2457.2019.35.053

0 引言

力学课程作为大学工科院校的专业必修课程，旨在培养大学生的工程理念，解决工程中的实际问题和提高工程师的综合素质。当前教育界也在呼吁要培养学生的创新意识和实践能力，面对越来越减少的课时和“卓越工程师培养计划”的需求[1]，迫切需要教师快速适应教育形式的发展，从有传授知识技能的培养转向重视学生工程素质创新能力的主动学习方式转变。在实际教學的过程中，表现出的具体问题是，学生不主动思考，仅限于接受知识，看例题解答习题，知识应用很机械，稍改变边界条件就出问题，不会综合运用所学力学知识去分析问题、解决问题。如何提高学生的学习兴趣和激情，引导和培养学生的创新意识和工程素质等已引起了力学教育工作者的思考[2]。力学教学中的一题多解是指根据已知条件从不同的角度和知识系统去探求解题的不同思路[3]。一题多解能揭示基本概念所延伸的基本技巧，使知识形成完整的体系，不仅能帮助学生掌握从表面看似不相关的定理、核心知识点及解题步骤，加深对知识点的理解和掌握，而且能培养学生发散思维，有效提高学生思维的活跃性、灵敏性，激发学生的学习兴趣和创新意识[5]。笔者以教材中的一道习题的求解问题为例，归纳总结不同求解方法的原理、核心知识点和解题步骤，深刻理解各种理论方法的内容、应用条件、应用场合和特点，从而深化、活化各基本概念和基本规律的认识，提高学生分析问题和解决问题的能力。

1 问题和解法

1.1 问题示例

如图1所示，梁BD为刚体，杆1、杆2与杆3的材料与横截面面积相同，在梁BD的中心C，承受铅垂载荷F作用，计算C点的水平与铅垂位移。已知载荷F=20KN，各杆的横截面面积A=100m2，弹性模量E=200GPa，梁长l=1000mm。

在授课过程中，学生的难点体现在对于这种杆系，不理解杆的伸长量与位移之间的关系，不会画杆系的位移。

1.2 利用威利奥特图解法

将图1所示的结构的三根杆截断，轴力分别为FN1，FN2，FN3，如图2。利用平衡条件

∑Fx=0，FN2cos45°=0

∑MB=0，FN3l-■F=0

∑Fy=0，FN1+F3+FN2sin45°-F=0

可得各杆的轴力

FN1=10KN;FN2=0;FN3=10KN

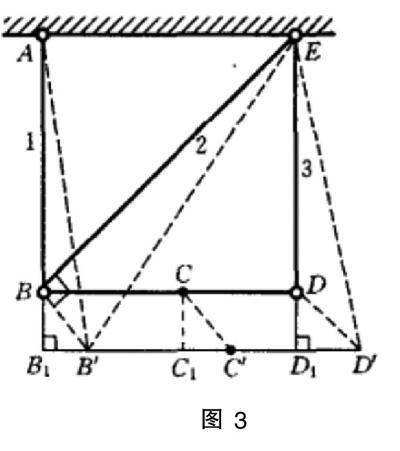
因杆2不受力，所以在外力F作用下，杆2不变形，只是随杆1、3的变形而绕铰接点E做刚体转动，使点B移动到点B'，如图3，杆1和杆3的轴力相等，所以它们的伸长也相同。由胡克定律有：

ΔL1=ΔL3=■=5×10-4m

变形后，刚性梁的新位置B'D'也就确定了，从而力F的作用点C的新位置C'也可确定，严格地说，点应该是以点E为圆心，以杆2即EB为半径划圆弧，与以点A为圆心，以杆1变形后的长度及AB1为半径划圆弧的交点，但由于是小变形，应用威利奥特图解法，点可由过点B作EB的垂线，与过点B1作AB1的垂线，两垂线的交点便确定了点B'，如图3。由图中的集合关系可知，点B的铅垂位移BB1等于其水平位移B1B'，等于杆1的拉伸变形Δl1，由于刚性梁BD因杆1和杆3的变形只作刚体平移，所以力F的作用点C的铅垂位移和水平位移与点B相同，即

ΔCx=Δl1=0.5mm（→）

ΔCy=Δl1=0.5mm（↓）

1.3 利用功能转换原理

设在外力F作用下，力F的作用点的铅垂位移为ΔCy，则外力作功为

W=■FΔCy

在求出三根杆的内力后，如图3所示结构的应变能为

Vt=∑■=■+■=■×2=■

根据功能转换原理，有

W=Vt，■FΔCy=■

所以力F的作用点C的铅垂位移为

ΔCy=■=■=5×10-4m

力F的作用点C的水平位移与铅垂位移相等，其分析与解法相同。

2 课堂效果评价

课堂教授两种方法以后，提示大家这类题目还有更多的解题思路，例如卡式第二定理法，基于虚位移原理的能量法来计算杆系结构位移计算;例如单位力法，作为能量法的另一种表达方式，单位力法主要用于求解线弹性位移;例如在能量法的教学过程中，利用单位力法推导出摩尔积分法，本题作为小变形的线弹性杆系结构，能否应用等等。

学生的反馈很好，很多同学重新返回到知识点章节，主动学习，寻找解决办法。问题解决了，知识点掌握了，知识点间的联系也深刻理解了。更重要的是他们开始主动学习思考了。

3 结语

本文以工程力学教材习题中的一道习题为例，给大家讲述了一题多解的教学方法，归纳总结了威力奥特图解法，功能转换原理，并引导学生尝试了卡式定理、单位力法等多种求解方法的原理，涉及了力学课程中多个知识点，小变形放大图、以切代弧、内力计算、胡克定律、应变能和能量原理等。通过一题多解，学生能主动去学习，思考应用已学的力学知识解决同一个问题，把各章节学到的零散的、互不相关的知识点，通过思考、应用，把握各方面知识的联系，形成一个完整的知识结构。一题多解能够打破学生平时解题形成的一种先入为主的思维定式，培养学生的创新思维能力。

【参考文献】

[1]林健.卓越工程师创新能力的培养[J].高等工程教育研究，2012（5）：1-17.

[2]余志红.教学与科研结合的力学课程的设计探索[J].科技视界，2019（6）：32-34.

[3]张淑芬，梁斌，杨民献.力学课程教学应突出学生素质培养[J].洛阳理工学院学报（自然科学版），2008（1）：91-93.

[4]蔡传国.本科力学实验中的创新思维培养方法探索[J].力学与实践，2013（6）：95-96.

[5]孙训芳，方孝淑，关来泰.材料力学（I）[M].第5版.北京：高等教育出版社，2009.10.

[6]曲艳东，贾艳东，孔祥清，等.材料力学一题多解谈创新[J].辽宁工业大学学报（社会科学版）.

[7]单辉祖，谢传峰.工程力学（静力学与材料力学）[M].北京：高等教育出版社，2004.1.