基于D-H矩阵的六足机器人运动仿真与分析

李胜铭 朱碧珂 王秉奇 吴振宇

摘 要：六足机器人具有较好的多地形适应能力，常用于勘测、侦察等人类无法完成的工作。针对其足数较多，控制算法复杂的问题，从单足的运动控制开始，建立描述其运动规律的D-H矩阵，计算出运动学方程。通过求解单足运动学方程的正解，建立机器人单足运动学模型，通过ADAMS实验仿真，得出六足机器人各关节在不同坐标系下的位移、角速度变化规律。最后对六足机器人的直线行走、转弯步态进行分析。该方法具有结构清晰、计算简单的优点，可为六足机器人的运动控制提供解决方案与参考。

关键词：D-H矩阵;六足机器人;运动学模型;步态;运动仿真;ADAMS实验

中图分类号：TP242.6文獻标识码：A文章编号：2095-1302（2019）12-00-05

0 引 言

随着人类对未知活动空间的不断探索，机器人已成为一种强大而有效的工具。从人类进步与发展的角度看，这种可自由移动、自动执行工作的机器装置，或将成为21世纪最具活力与创造力的领域之一，它将带来巨大的社会与经济效益[1]。

在众多可移动机器人系列中，足式机器人能够更好地适应多种地形条件，在不规则地形下的平稳性更好，有能力隔离不规则地形。此外，相对于轮式及履带式移动方式而言，足式对环境的破坏较小，机动性能及燃油经济性更好[2-3]。在庞大的足式机器人家族中，根据足数的不同可分为单足、双足、三足及四足、六足、八足机器人等。

在足式机器人运动过程中，必须进行运动学分析，保证其按照规定路线移动，同时维持本身动平衡[4]。因此，机器人身体上的每一个运动结构均需要精准的控制算法和调节方式。六足机器人的每条单足均由三个关节（股部、大腿、小腿）通过转动副的形式串联而成，构成具有三个自由度的空间连杆机构[5]。传统利用几何关系法推导执行器与控制端的位移关系，或在大地坐标系内建立方程，表示每个关节相对于基坐标的运动规律。然而，运动方程均比较复杂[6-7]。本文采用D-H参数法，使用4×4矩阵描述两个相邻关节空间坐标系之间的关系，层层递推，利用矩阵变换，得到末端执行器相对于基础坐标系的位置与运动的变换方程。该方法可将一个空间矢量从一个坐标系变换到另一个坐标系中，清晰地描述低副机构的运动，并可十分方便地应用于机器人学[8-9]。通过建立合适的参考坐标系，对每个关节的运动轨迹与运动状态进行求解，从而确定各个构件的运动参数。

1 机器人单足D-H参数法

本文使用Inventor软件对六足机器人的单足进行建模，其三维结构模型如图1所示。

图1中，关节1与机体基座、关节2与关节1、关节3与关节2分别通过舵机A，B，C相连，且均构成转动副，关节3为末端执行器[10]。

根据D-H参数法要求，建立参数坐标系，如图2所示。

根据机器人单足实际运动规则可知，在该坐标系中，坐标系{1}与坐标系{0}在X-Y平面内共平面;坐标系{2}与坐标系{1}在X-Z平面内共平面;坐标系{3}与坐标系{2}在X-Z平面内共平面。由此可化简变换方程。

建立坐标系后，在新的坐标系中标注连杆参数，如图3所示。

连杆i-1的长度ai-1：关节轴线i-1与关节轴线i在坐标系{i-1}中的公垂线长度。

连杆i-1的扭角αi-1：关节轴线i-1与关节轴线i的夹角。

连杆偏距di：坐标系{i-1}与坐标系{i}内的Xi-1轴与Xi轴在Zi轴上的距离。

连杆关节转角θn：坐标系{i-1}与坐标系{i}内的Xi-1轴与Xi轴在Zi轴的夹角。

以上条件中，i取1，2，3。

根据所设计的机器人单足系统中的硬件结构与几何条件，获得a0=20 mm，a1=74 mm，a2=88.2 mm。并以此填写机器人单足D-H参数表，见表1所列。

2 机器人单足运动学正解

基础坐标系{0}为机器人基座所在坐标系，静态时与大地坐标系重合。坐标系{1}为关节1末端所在坐标系，从坐标系{0}到坐标系{1}的齐次变换矩阵为：

坐标系{2}为关节2末端所在坐标系，从坐标系{1}到坐标系{2}的齐次变换矩阵为：

坐标系{3}为关节3末端所在坐标系，从坐标系{2}到坐标系{3}的齐次变换矩阵为：

从机器人执行末端坐标系{3}到起始坐标系{0}的总变换矩阵为：

由此得到机器人单足运动学正解方程。

其中：

式中：cn=cos θn;sn=sin θn。

该模型中，所有运动副均为旋转副，因此所有未知变量均为角度变量。选取确定的角度参数代入矩阵T03中，得到该参数下机器人单足末端坐标系{3}到基坐标系{0}的总变换矩阵，即该机器人单足运动学方程正解。由于初始状态已知，因此可得到该足当前位姿。

3 机器人单足ADAMS仿真

利用三维实体仿真软件ADAMS对六足机器人单足结构进行三维建模，创建的模型如图4所示。图中PART1，PART2，PART3对应关节1，2，3。

参考蜘蛛等节肢动物的身体结构，利用ADAMS对机器人单足各关节比例进行仿真优化。同时，根据实际机器人大小（身体宽度），首先确定关节3，即小腿的长度为88.2 mm，套用公式并考虑到实际舵机各项参数，设定基节（关节1）长度为20 mm，利用ADAMS进行参数优化，求解得到大腿（关节2）长度为74 mm。

3.1 机器人单足各关节位移变化

单步运动中，分别对机器人单足系统中的三个关节在基础坐标系和上一关节末端坐标系内的位移变化拟合成曲线并进行分析。

3.1.1 PART1单步运动时分别在X，Y，Z轴方向上位移变化曲线在{0}坐标系内，位移随时间的变化曲线如图5所示。

由图5可知，在基础坐标系内，关节1在Y轴、Z轴方向上无位移变化，仅在X轴方向上产生位移。

3.1.2 PART2在X，Y，Z轴方向上位移变化曲线

（1）相对于基础坐标系（{0}坐标系），PART2各方向位移随时间的变化曲线如图6所示。

由图6可知，在基础坐标系{0}内，关节2在Z轴方向上产生较小的正向位移，而在X轴和Y轴方向上产生负向位移，其中Y轴方向上的位移幅度最大。

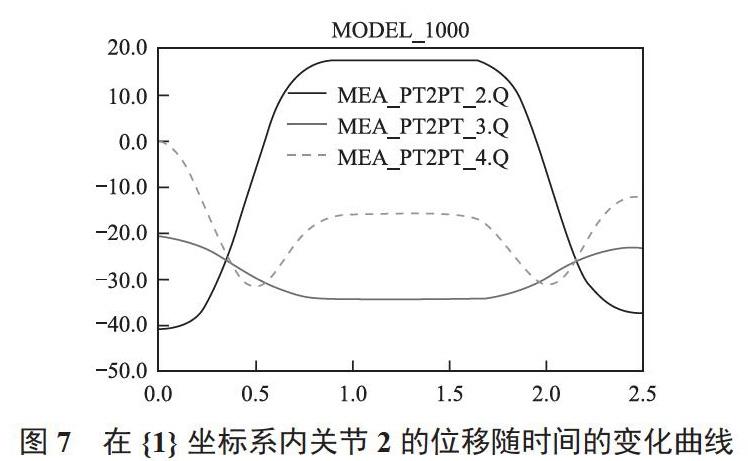
（2）在坐标系{1}内，即PART2质心在X，Y，Z轴方向上相对于PART1质心在X，Y，Z轴三个方向上的位移变化曲线如图7所示。

由图7可知，PART2质心相对于PART1质心在X轴方向上位移变化幅度最大;在Y轴方向上始终处于负向位移;在Z轴方向上先增大后减小，再增大后减小。

3.1.3 PART3在X，Y，Z轴方向上位移变化曲线

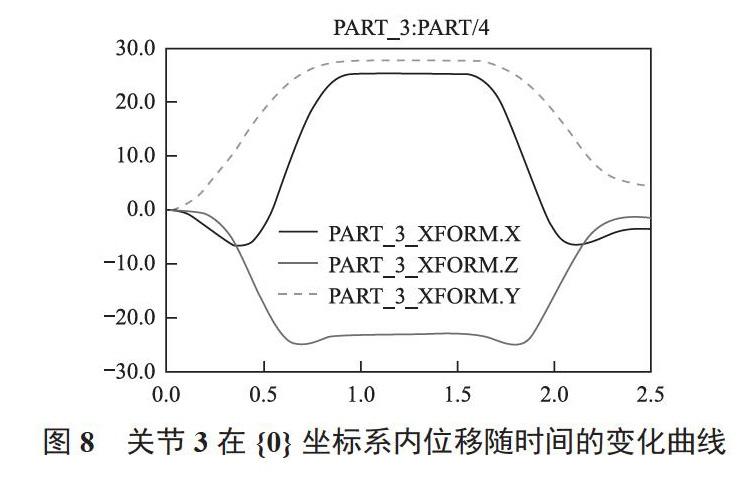
（1）相对于基础坐标系{0}，位移随时间的变化曲线如图8所示。

由图8可知，在基础坐标系{0}内，关节3在X轴和Y轴方向上产生正向位移，在Z轴方向上产生负相位移，位移幅值相近。

（2）在{2}坐标系内，即PART3质心在X，Y，Z轴方向上相对于PART2质心在X，Y，Z方向上的位移变化曲线如图9所示。

由图9可知，PART3质心相对于PART2质心在X，Y，Z轴方向上位移变化幅值相近。其中，在Y轴方向上始终处于正向位移;在Z轴方向上先增大后减小，再增大后减小。

3.2 机器人单足各关节角速度变化

单步运动中，对单足的三个关节，分别在基础坐标系内和上一关节末端坐标系内的角速度变化拟合成曲线并进行分析。

3.2.1 PART1在X，Y，Z轴方向上角速度随时间变化曲线

关节1在{0}坐标系内角速度随时间的变化曲线如图10所示。

由图10可知，关节1相对于基础坐标系，在X，Z轴方向上均无角速度的变化;仅在Y轴方向上，其变化方式为角速度先反向增大后减小，再正向增大，最后减小到0。

3.2.2 PART2在X，Y，Z轴方向上角速度曲线

（1）PART2的质心相对于基础坐标系{0}，角速度随时间的变化曲线如图11所示。

由图11可知，关节2相对于基础坐标系，在X，Z轴方向上角速度变化较小;在Z轴方向上角速度变化幅度较大，先反向增大后减小，再正向增大，最后减小到0。

（2）在{1}坐标系内，即PART2的质心在X，Y，Z轴方向上相对于PART1的质心在X，Y，Z轴方向上的角速度变化曲线如图12所示。

由图12可知，关节2的质心相对于关节1的质心，在Y轴方向上角速度变化较小;在Y轴和Z轴方向上角速度变化较大。

3.2.3 PART3在X，Y，Z轴方向上的角速度变化曲线

（1）在基础坐标系{0}内，PART3质心的角速度随时间的变化曲线如图13所示。

由图13可知，关节3相对于基座，在X，Z轴方向上角速度无变化，在Y轴方向上先增大后减小，再反向增大后减小。

（2）在{2}坐标系内，即PART3的质心在X，Y，Z轴方向上相对于PART2的质心在X，Y，Z轴方向上的角速度曲线如图14所示。

由图14可知，关节3的质心相对于关节2的质心在Y轴方向上角速度无变化;在Y轴和Z轴方向上角速度同时发生变化并同时结束。

4 仿生六足机器人常规步态分析

得到六足机器人单足的运动学方程后，进一步对六足步态进行规划和分析，最终可得到六足机器人全部关节的配合方式，如图15所示。

六足机器人采用稳定的三角步态方式行走。足1，4，5保持同步，足2，3，6保持同步;两组足轮流抬起或着地。因此，六足机器人每条腿上均安装三个舵机，其中两个控制其与地面平行平面内的运动，另一个控制腿的抬起动作。

4.1 直线行走步态分析

直行步态如图16所示，圆圈表示机器人六条腿部上的舵机。从图15可知，机器人六足交叉构成两个三角形，同一个三角形中的三足保持相同的抬起或着地状态。

当机器人直线行走时，假设Aa，Dd，Ee三足着地，Bb，Cc，Ff三足悬空，着地的三足控制机器人平行移动，即A，D，E舵机转动，使机器人产生水平位移;悬空的三足对位移没有直接影响，但B，C，F舵机仍然转动，为下一次支撑做准备。

4.2 转弯步态分析

转弯步态如图17所示。

转弯时以内侧中间足（足3）为中心。在整个转弯过程中，只有足2，3前后摆动，其余均不作摆动，只做上下抬起运动。图17中，足2，3，6先抬起，其中足2，6向前摆动，接着足1，4，5抬起并保持不动，足2，6向后摆动。

5 结 语

通过本文仿真可以看出，相较于传统单一坐标系推导运动学方程，采用D-H参数法，利用矩阵变换、坐标系的转化求解机器人运动学方程思路更清晰，且运算更简便。D-H参数法为多关节串联类仿生机器人运动学方程的建立与求解提供了新的思路与方法[11-13]。

本文对于六足机器人，从单足开始分析，定义不同坐标系中的各个参数，建立起基于D-H参数的空间坐标系，并列出D-H参数表，推导出机器人单足步态运动学正解，得到机器人各关节末端执行器与基座控制端的矩阵关系。经过ADAMS仿真，可得出单步中各个关节在不同坐标系下运动轨迹与角速度的变化图像，进而分析机器人步态，为实现六足机器人步态控制提供理论指导，具有简洁高效的优点。

参 考 文 献

[1]甘屹，王均垒，孙福佳.基于给定工作空间的6R型机器人D-H参数优化设计[J].中国机械工程，2014，25（22）：3003-3007.

[2]林少丹，傅高升，李俊达，等.串并联结构工业机器人D-H参数建立及算例[J].三明學院学报，2017，34（2）：35-41.

[3]项有元，陈万米，邹国柱.基于D-H算法的自主机器人机械臂建模方法研究[J].工业控制计算机，2014，27（7）：113-115.

[4]朱国杰，田文凯，吕承哲，等.六足仿生机器人机构与控制系统设计[J].测控技术，2017，36（1）：55-58.

[5]刘琰，郑璐颖，孙浩洋，等.三角步态下六足机器人运动分析[J].青岛大学学报（工程技术版），2018，33（3）：38-42.

[6]张晴晴，谢傲，龚智强.基于D-H矩阵的挖斗可偏转挖掘机工作装置运动学建模与分析[J].绥化学院学报，2018，38（6）：141-144.

[7]莫毅.基于六自由度工业机器人的D-H模型及仿真分析[J].机床与液压，2017，45（11）：64-68.

[8]高瑞翔，杨青，房鹤飞.基于改良的D-H模型的机器人运动参数标定方法[J].上海计量测试，2018，45（z1）：48-50.

[9]张博.基于D-H坐标系法的机器人运动学研究[J].电子科技，2016，29（6）：154-156.

[10]康之讷.论基于单片机的六足机器人自动避障控制系统[J].数字技术与应用，2018，36（12）：13-14.

[11]谢靖.基于单片机的六足机器人自动避障控制系统研究[J].无线互联科技，2018，15（9）：45-46.

[12]孔令文，李鹏永，杜巧玲.基于模糊神经网络的六足机器人自主导航闭环控制系统设计[J].机器人，2018，40（1）：16-23.

[13]李嘉琪，陈海彬，钟辉，等.基于D-H矩阵计算的工业六轴机械手末端定位的精准度[J].机电工程技术，2018，47（9）：75-77.