振铃型干扰信号完整性补偿方法研究

贾新强 熊天毅

摘 要：对于电子产品普遍存在信号完整性干扰问题的现状，以较为典型的振铃型干扰信号为对象，通过严格的信号完整性分析，研究了一种基于阻容特性匹配的方法。通过对振铃型干扰信号进行有效成分的优化，简单有效地改善信号波形，降低因为信号完整性问题导致故障代价的可能性。通过基本数学模型的建立，定位信号干扰来源，分析信号传输路径阻抗分布，计算阻性阻抗和容性阻抗匹配的理论数值，达到消减信号反射和增强衰减阻尼的目的。经过对比试验，验证了所提研究思路及方法的正确性和可行性。

关键词：振铃型干扰;信号完整性;阻抗匹配;数学模型;故障代价;传输路径阻抗分布

中图分类号：TP39文献标识码：A文章编号：2095-1302（2019）12-00-02

0 引 言

当前随着航空机载电子技术的快速发展，在机舱内部，诸如有源相控阵雷达等高频大功率设备和精密电传数字控制系统，不同频率范围、不同功率等级的数字与模拟信号之间存在密集空间内的信号互扰，导致较多破坏信号完整性的问题出现，如计算机指令接收错误、虚警报故、功率开关误动作、伺服闭环控制系统失稳等，严重者会直接影响飞行安全。

为此，本文针对较为常见的振铃型干扰，着重解决信号反射和高频振荡杂波的技术难点，力求以简便可操作的方法，实现信号完整性的补偿改善[1]。

1 干扰来源和原因分析

所有数字信号在物理层面依然属于模拟信号，在其生成过程中，必然存在CMOS电路开关通断形成的斩波动作，信号在产生源头就会引入高次谐波干扰;此外，信号在传输过程中，因为物理空间的约束和工艺水平的限制，不可避免地会接收到来自信号外部的扰动。因此可以认为，在现阶段的电子技术水平下，信号干扰的出现是必然的。

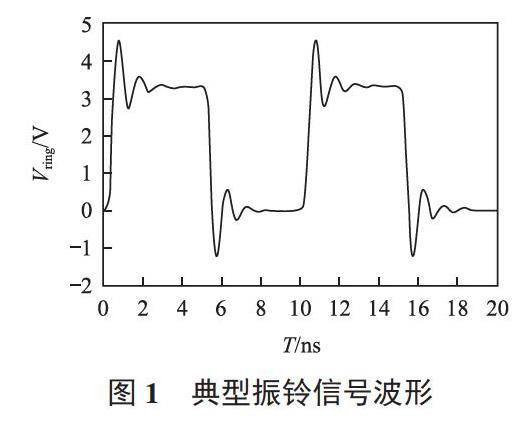
振铃型干扰信号是最为常见的信号干扰类型之一，它在波形中同时包含了超调和振荡的影响。图1所示为典型的信号振铃现象。

根据经典电路基础理论，信号传输路径上的阻抗不连续性会引发信号的局部反射效应;从具体电路简化归纳出的电路模型在输出端的阻尼比不足，导致信号上的叠加谐波衰减过慢。而这两种因素构成了振铃型干扰信号形成的主要原因。本文将围绕如何消减反射和增强阻尼，讨论分析针对振铃型干扰信号的完整性补偿方法[2-4]。

2 消减反射的信号处理

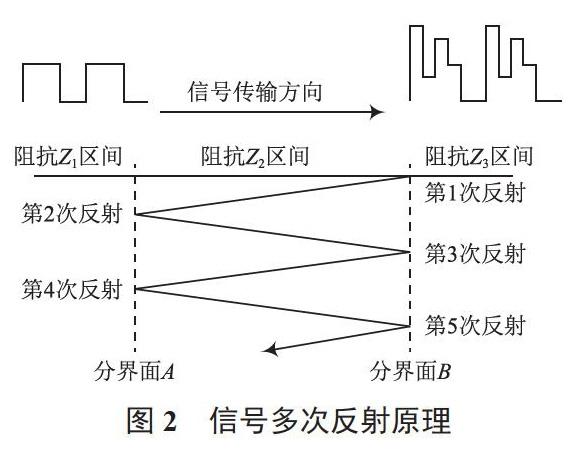
从物理层面描述，电路信号是以电磁波的形式在介质中沿某一方向传输。由于介质的材料、特性以及邻近环境的不同，信号传输路径上的介质阻抗存在差异，造成传输阻抗的不连续性。信号抵达阻抗不同的传输线分界面时，一部分以入射电压继续正向传输，一部分则以反射电压沿原路径反向传输，在阻抗分界面处，入射与反射电压叠加，形成该处的实际信号电压，与抵达前的信号电平产生差异，而如果连续经过两处不同阻抗的传输分界面，则信号会在两处之间发生多次反射，形成更为復杂的信号电平，如图2所示。

发生在B点的第一次反射，测量电压值为5.5 V，认为末端接收器件输入阻抗为理想无穷大，得到B点反射系数：

即发生等压反射，则推导得到输入电压为5.5 V/2=2.75 V，发生在B点的第三次反射，测量电压值为1.84 V，即以反射系数1为基础再次发生等压反射，推得此次输入电压为（1.84-5.5）/2= -1.83 V而这是由2.75 V在折返A点发生第二次反射时产生的，由此得到A点反射系数：

通过A，B点反射系数得到Z1，Z2阻抗关系，即

Z2=5Z1。

根据PCB印制线的特性阻抗经验公式，单位长度电感为9.009 nH/inch，单位长度电容为3.585 pF/inch，则测量Z1阻抗区间印制线以10 inch长度计算，有下式：

由于我们的目标是尽可能使得反射系数ΓB消减至接近0，即在信号传输末端增加并联匹配电阻，使得Z3尽可能接近Z2=5Z1=5×50.13 Ω=250.65 Ω。这样就能够从原理上改善波形在传输中在阻抗分界面发生反射形成振铃的问题。

因此，消减反射信号可以采用在传输路径末端阻抗分界面处并联合适的匹配电阻这一方式。

3 增强阻尼的信号处理

信号在传输过程中不可避免地会因外部环境扰动而引入谐波杂质，无论是在产生起始端，还是在后级接收端，只要端口状态发生变化，一般都会出现高次谐波振荡的现象。为了消除谐波影响，常见的方法是增强对特定谐波成分的阻尼设计，使得谐波在短时间内迅速衰减，从而改善有用的信号波形[5-7]。

典型信号传输电路如图3所示。

推导得到电路模型传递函数：

由传递函数得到电路阻尼比计算式：

根据阻尼比公式，可知R越大，系统的阻尼比越小，越容易振荡，而在电路中运放的阻抗非常大，这将导致系统的阻尼比接近0，所以传感器输出波形较差。

若要使系统阻尼比尽可能接近0.707，得到比较良好的波形，即

那么可以计算得到：

需要在输出端并联电阻，使得等效电阻约为177.26 Ω，如此形成与反射系数接近1的匹配阻抗阻值之间的差距，使用末端匹配电容的方式予以补偿。

假设并联电阻为250 Ω，由阻尼比公式推得：

考虑到实际系统与理想情况的差异，可以认为传感器输出端增加并联250 Ω电阻和3.6 pF电容，使得阻容协调之后的系统阻尼比接近0.707，能够从原理上改善波形在传输中面对的高次谐波振荡问题。

4 方法验证及结果分析

为了验证上述振铃型信号完整性补偿方法的有效性和可行性，在方波解调输入信号上进行应用验证。电路改进优化前的实测信号如图4所示。

通过在信号传输末端匹配电阻降低反射系数，以及在信号传输末端匹配电容约束阻尼比后，信号在最大超调、调整时间、振荡次数、稳定误差等方面均有显著改善，对比数据见表1所列。

电路改进优化后的实测信号如图5所示。

通过对比可知，该信号补偿优化方法得到成功验证，作为伺服控制的重要技术积累，为解决电子部件传输信号完整性问题提供了可行方案。

5 结 语

本文研究了振铃型干扰信号完整性补偿方法，通过对信号传输完整性干扰来源及原因进行分析，建立电路数学模型，计算消减反射和约束阻尼比，并经过实际电路验证，获得了明显优化的信号，有效补偿、改善了振铃型干扰信号的完整性。

参 考 文 献

[1]于争.信号完整性揭秘—于博士SI设计手记[M].北京：机械工业出版社，2013.

[2]Eric Bogatin著.信号完整性分析[M].李玉山，李丽平，等译.北京：电子工业出版社，2005.

[3]陈非凡.工程测试技术[M].北京：清华大学出版社，2006.

[4]张洪润，张亚凡.传感技术与应用教程[M].北京：清华大学出版社，2005.

[5]佟星元，朱樟明，杨银堂，等.信号完整性设计中的抖动与振铃消除技术[J].西安电子科技大学学报（自然科学版），2012，39（6）：136-142.

[6]冯非，王超，艾铁柱.机载计算机电源系统稳定性研究[J].物联网技术，2017，7（6）：109-111.

[7]张兰勇，杜逸璇，郁嘉宇.板级设备的电磁干扰及信号完整性研究[J].新型工业化，2015，5（2）：48-53.

[8]姜攀.板级信号完整性、电源完整性和电磁干扰研究[D].呼和浩特：内蒙古大学，2015.

[9]姚琴琴，谢锐，马铁华.高速信号采集及存储系统的信号完整性研究分析[J].弹箭与制导学报，2015，35（1）：177-180.

[10]曹世伟.高速电路中的信号完整性和电源完整性研究[D].西安：西安电子科技大学，2015.