考虑垂度影响的斜拉桥索力与频率间关系分析

徐建铭 刘文会

（吉林建筑大学交通科学与工程学院， 吉林 长春 130021）

索力监测是斜拉桥施工控制的重要内容，实际的拉索具有一定的抗弯刚度。若忽略垂度和抗弯刚度的影响，用简单的弦理论计算索力，将带来很大的误差。为准确使用振动法测定索力，必须考虑这些因素。1974年，Irvine抛弃了不可伸长的假设，系统地考察了索的弹性效应，发现了模态超越(modal crossover)现象[1]。至此，小垂度水平索的线性动力特性问题算是得到了解决。在工程中为了提高工作效率，有必要推导由频率求解索力的简单准确的实用公式。

1 考虑索垂度和弹性对自振频率影响的解析理论

1.1 假定条件

拉索忽略弦向的自重分量；拉索垂跨比小于 1:10；索等截面，均质线弹性；索横截面面积保持不变；不计抗弯刚度；索只在横截面产生法向应力并在截面上均匀分布；索作微幅自由振动。

拉索索力计算公式

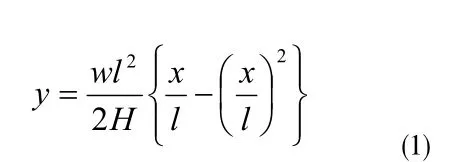
静力下的力学模型

索作微幅振动，其运动方程：

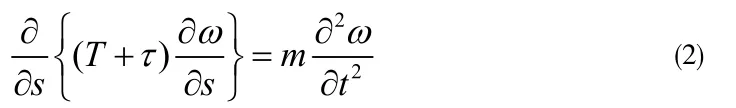
其中：H-索力的水平分量，w-单位长度索重，u是面内纵向运动分量，v是面内竖向运动分量，ω是面外运动分量，τ是由于运动引起的索力增量，T -索的拉力

在小垂跨比的假设条件下索的线形振动的方程：

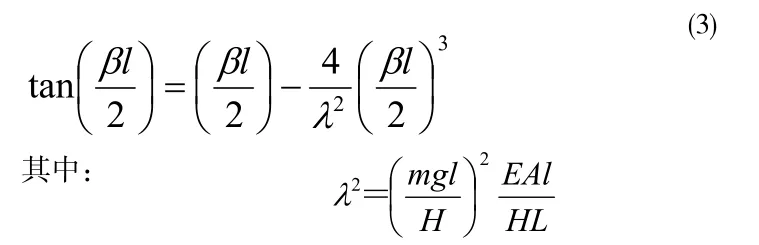
方程(3)第一项反应索的几何形状，第二项反应了索的弹性。

2 索力计算的实用公式

2.1 公式推导

由方程解得：

由于已有索的经验公式 T= 4ml2f2则寻找并建立α与f的关系函数。

2.2 非线性回归分析

应用Origin5.0软件采用ExpAssoc指数函数进行回归分析。回归模型为：

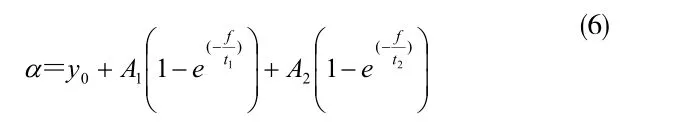
将试验结果代入上式，求索力，与实测值对比，验证回归公式的准确性及实用性。

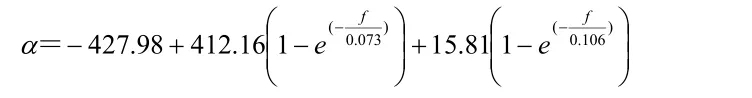
公式(5)变换为：

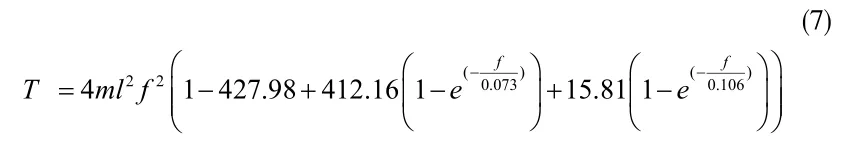
有限单元法数值分析

通过ANSYS建立了空间索单元模型。索采用link10单元类型，每根索划分为20个单元，索两端节点在X,Y,Z方向施加约束。对索模型进行静力分析及模态分析。分析模型如图2及C18索的各阶振型如下：

3 数值计算结果分析

目前在工程中工程师通过采用频差作为索的基频值。计算索力的经验公式[2]为：

其中：Δf为以Hz为单位的频差。

4 结语

1.对反映拉索垂度对自振频率的影响特征参数进行了分析。参数分析的结果表明垂度对索自振频率的影响不能忽略。

2.对 Irvine公式进行变换，建立系数α与频率 f之间的关系，并辅以曲线拟合，得到了考虑索垂度影响的拉索自振基频与索力之间的显式关系，所有关系式与理论解的误差不超过3%。

3.推导出的由基频计算索力的实用公式，可供实践中参考。

5 结论

推导的计算索力公式(7)在实桥应用结果见表1，其形式简单结果准确。