基于支持向量回归的机器人操作臂轨迹规划

金啟媛，吴洪明，刘伟鹏

（武汉理工大学 物流工程学院，武汉 430063）

动态系统稳定性估计SEDS轨迹规划算法[1]于2010由Khansari-Zadeh等人提出，该方法首先对操作臂进行简单的示教动作，得到示教数据，然后通过高斯混合模型和李雅普诺夫稳定性判据得到稳定性约束条件，推导出产生类似轨迹的轨迹规划模型，并具备在整个空间内泛化的能力，即在任意一点，通过该轨迹规划模型都可以得到其运动速度。但采用高斯混合模型，其参数求解过程与其设定初值有很大关系，而初始值为随机值，因此对统一示教轨迹存在多组训练结果模型的问题，模型精确性也存在一定差异。支持向量机简称SVM，是Vapnik等人根据统计学理论提出的学习方法。SVM是以结构追求风险最小化为训练准则，故对小样本问题有较好的预测和泛化能力，且在处理非线性问题时引入核函数，巧妙地降低维度解决了复杂的计算问题。SVM根据应用不同，分为支持向量分类（SVC）和支持向量回归（SVR）。本文在原SEDS基础上，使用支持向量回归模型代替高斯混合模型对示范轨迹进行学习，以得到具有类似泛化能力且稳定收敛的轨迹规划模型。

1 基于SEDS的机器人轨迹规划

基于SEDS的轨迹规划的整体框架如图1所示。机器人的控制模型分为两层循环，内层循环指其控制系统的固有循环，外层循环为机器人的运动学建模，包括正运动学模块，而通过SEDS算法得到动态系统模块和逆运动学模块。

图1 基于SEDS方法控制机器人运动的整体框架Fig.1 Controlling the overall framework of robot motion based on SEDS method

SEDS算法中动态系统模块的表达式如下：

式中：：Rn→Rn表示一个非线性连续微分方程；x为操作臂末端位姿向量；˙为该位姿下末端的速度向量；θ表示模型所有参数。

在动态环境下，通过SEDS训练得到速度模型，该模型的输入为机器人末端执行器位姿，输出为该状态下的速度，对时间积分后求得下一步位置，再经过逆运动学获取机器人关节在当前位置的速度，由此来控制其运动轨迹[1]。

SEDS由示范编程结合稳定性约束条件推导得出，其原理如图2所示。示范编程方法指根据任务要求生成一条或多条示教轨迹信息，基于高斯混合模型建模，即未知映射由高斯混合模型拟合得到，通过该模型得到整个空间内任意位姿的轨迹。稳定性约束条件是以Lyapunov稳定性第二定理为依据，结合示范编程中的回归模型和选取的李雅普诺夫函数得到，用以保证模型在全局范围内的稳定性。

图2 SEDS原理图Fig.2 SEDS schematic

2 稳定多维SVR模型设计

2.1 支持向量回归模型

对于单维输出的训练样本，数据样本集（x1，y1），…，（xl，yl）∈Rn×R。 假设模型为线性，设回归函数为[2]

而回归估计中，最理想的情况为yi-（xi）=0。但通过部分数据进行拟合几乎不可能达到理想状态。因此引入ε不敏感损失函数判定回归估计模型有效性。当预测值与实际值相差小与很小的正数ε，则可认定估计模型（x）无损[3]。

当样本数据存在噪声时，可能会导致回归模型失败，故引入松弛变量 ξ=（ξ1，ξ2，…，ξl），以保证式（3）解存在，所得ε-SVR模型的优化目标函数为

式中：C为超参，决定回归模型的扁平度和对大于ε的偏差的容忍之间的均衡。

对于凸二次规划问题，利用拉格朗日乘子法去掉约束条件，再通过拉格朗日对偶性转化为对偶问题（此优化问题满足 KKT条件[4]），如式（4）所示：

对求极小问题的变量求极值：

由于 γi＞0，αi＞0，消去 γi，得到最终的优化目标函数：

对于非线性系统的回归估计，需借助核函数k（xi，x），将样本点的内积〈xi，xj〉转换为隐式映射后的内积〈φ（xi），φ（xj）〉，在高维特征空间中进行线性回归。在式（4）用SMO算法对变量取极值，求解出α，α*后，得到回归估计模型：

操作臂的轨迹规划是非线性回归问题，优先选用高斯径向基核函数σ为其带宽，K始终为半正定矩阵。故单维回归模型可表示为

2.2 于自定义核函数的多维输出SVR

多维输出的SVR是单维输出SVR的叠加，根据式（8）得，多维模型表示为[5]

为分析非线性系统稳定性问题，常采用李雅普诺夫稳定性第二定理，即存在一个连续以及连续可微的李雅普诺夫候选函数v（x），并满足：

式中：x*是=f（x；θ）的吸引点，即目标点[6]。

在SEDS方法中，从运动势能的角度考虑，越靠近目标点势能越小，以x表示机器人末端的当前位姿，取李雅普诺夫函数为

此时目标点在原点处，即v（x*）=0。显然满足条件1和3，对于条件2：

式中：α= [α …α]Ti1nσ= [σ1…σn]T；B=[b1…bn]T。

将˙（x）转化为二次型，需借助核函数的性质：若k1为核函数，则对任意函数g（x），k（x1，x2）=g（x1）·k1（x1，x2）g（x2）是核函数[7]。 x 是n维向量，对 x 中的任意一维xj，设g（x）为x与n维空间中表示该维的基pj的乘积，同时k1为高斯径向核函数，则新得到的核函数为

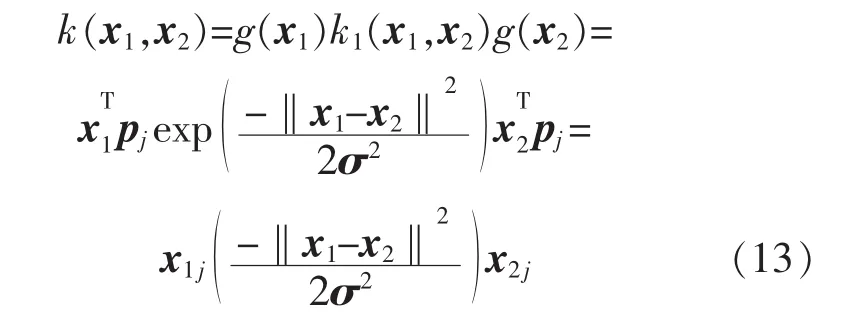
带入回归模型中，对于第j维输出：

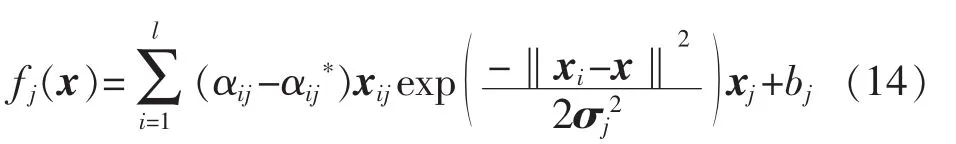
故有：

式（15）中，取加数中的第j项：

要保证上述表达式小于0，则应满足：

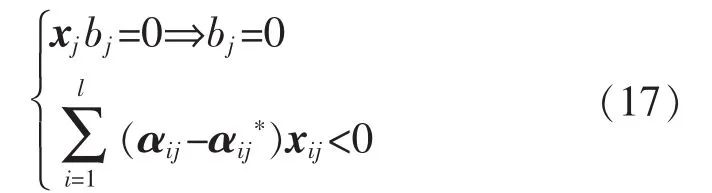
添加这2个约束条件，使得第j项小于0。由此类推，可保证等式（16）右边至少有一个加数小于0，其他项小于等于0，进而保证等式左边的和小于0。非支持向量对应参数为零，所以仅需考虑支持向量，设SV为支持向量集由此可得全局范围内的稳定性约束条件为

由约束条件可得，回归模型中偏置项B只能取0向量，模型变为多维无偏SVR模型，因此基于多维支持向量回归的SEDS轨迹规划模型为

3 基于多维SVR轨迹规划模型仿真分析

对基于SVR的SEDS进行仿真分析时，其算法是在林智仁教授开发的libsvm基础上改造的，仿真数据来自LASA原有的二维数据。本例中，目标函数中模型扁平度与偏差的容忍值之间的权重C和核函数中的参数σ以及ε带宽度是需要预设的量。为明确参数对模型的影响，采用原SEDS模型提供的二维字母C型示教数据进行预设参数的寻优。采用K折交叉验证法，验证参数取5，两个参数的变化范围为2-8～28之间，变化步长为20.4，确定C和σ的最优值，以获得最小均方差MSE，结果如图3和4所示。

图3 ξ1权重C和核函数中的参数σ对应MSE Fig.3 ξ1weightand C parameters σ in the kernel function corresponding to MSE

图4 ξ2权重C和核函数中的参数σ对应MSE Fig.4 ξ2weightand C parameters σ in the kernel function corresponding to MSE

ε对权重C与参数σ变化不敏感，需要不断地手动调试[8]。实验中ε取值在0.1～4之间步长为0.5左右变化，如图5所示，经调试当ε取1.5时，对示教轨迹有较高的拟合程度，向目标点收敛，同时具备较好的全局泛化能力。

以学习2维输出时的C形轨迹为例，全局轨迹规划模型对比如图6和7所示。

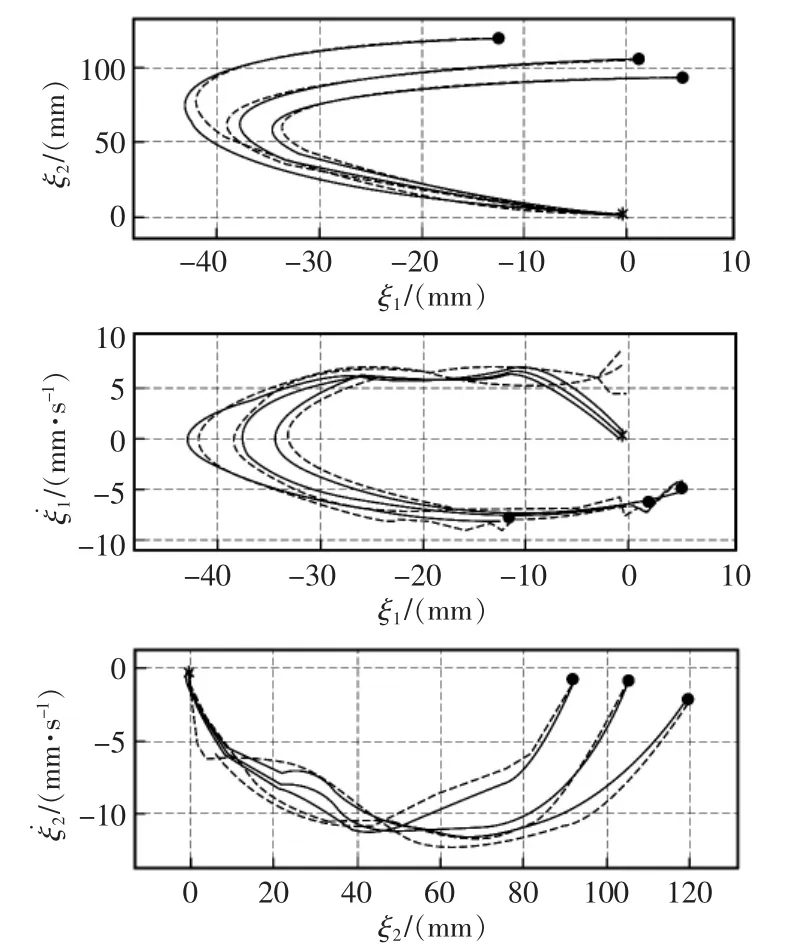
图5 示教轨迹再现对比Fig.5 Teaching track reproduction contrast

图6 原SEDS全局轨迹规划模型Fig.6 Original SEDS global trajectory planning model

图7 基于SVR的SEDS全局轨迹规划模型Fig.7 SVR-based SEDS global trajectory planning model

由对比图可得，基于SVR的SEDS具有和原模型类似的泛化能力，稳定性约束条件的存在使得轨迹能稳定收敛，不存在局部区域无法收敛的情况。且对比两图中示教轨迹的左侧区域，基于高斯混合模型的SEDS的规划轨迹有所偏离，而基于SVR的SEDS仍能保持C形轨迹，故其泛化轨迹的轮廓比原SEDS有一定的提升。

4 结语

本文从改变SEDS学习算法的角度，设计了新的基于支持向量机的稳定的轨迹规划模型，得到了与原模型类似的泛化能力，且改善了局部区域的C型轨迹，并仿真验证了模型的可行性，使其能应用于服务机器人操作臂的轨迹规划中。但由于需事先确定预设参数值，这个优化过程耗时较长，轨迹规划的便捷性会收到一定程度的限制。故下一步需要对初始参数的选择做研究。